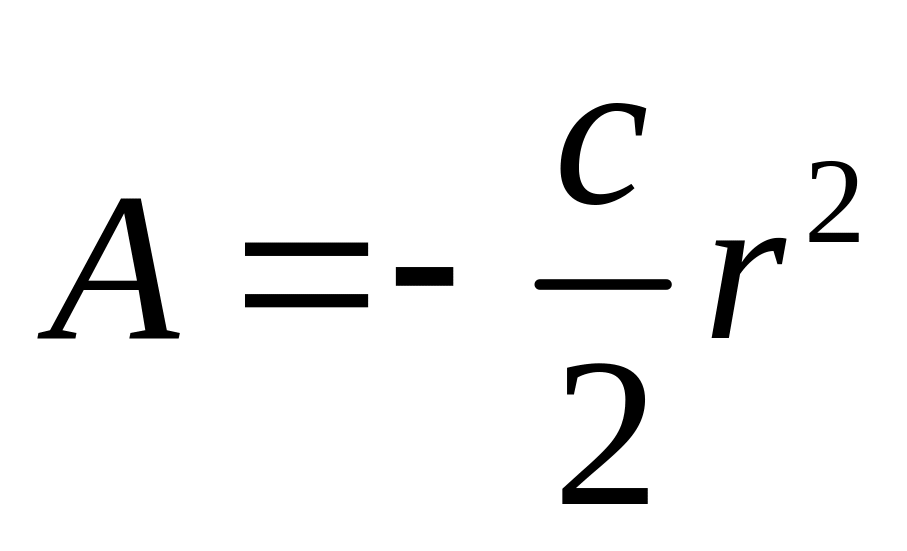23. Поверхности уровня и их свойства.

Поверхность

на которой силовая функция U имеет постоянное значение, называется эквипотенциальной поверхностью или поверхностью уровня.

1. Если начальная и конечная точки расположены на одной и той же поверхности уровня, то работа силы стационарного потенциального по перемещению материальной точки из начального положения в конечное равна нулю.

т.к.

2. Сила потенциального поля направлена по нормали к поверхности уровня в сторону возрастания силовой функции U.

24. Примеры вычисления силовых функций однородного поля силы тяжести и линейной силы упругости.

Однородное поле силы тяжести

Рассмотрим материальную точку массой m, находящуюся в однородном поле силы тяжести. Направим ось Oz вертикально вверх, а оси Ox и Oy произвольно в горизонтальной плоскости.

Проекции силы тяжести на оси координат будут равны

Элементарная работа силы тяжести

Так как элементарная работа силы тяжести является полным дифференциалом и , то, интегрируя, находим

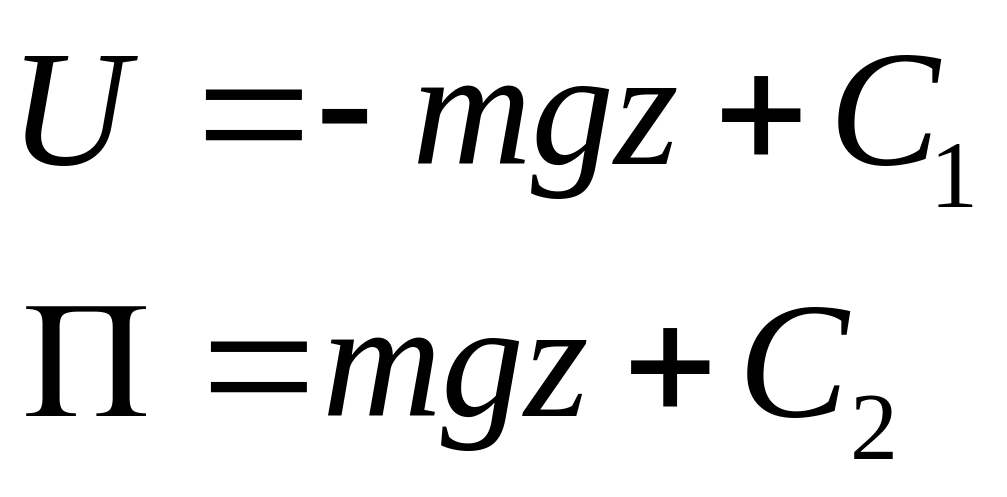(I)

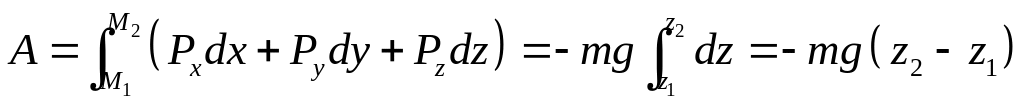
Где А – работа силы тяжести материальной точки массой m на перемещении . (I) можно представить в виде

Где - высота подъема точки.

Если точка расположена выше , т.е. опускается, то работа положительная, иначе – отрицательная.

Поле линейной силы упругости.

Лиин. сила упр. подчиняется закону Гука

Элементарная работа этой силы:

так как 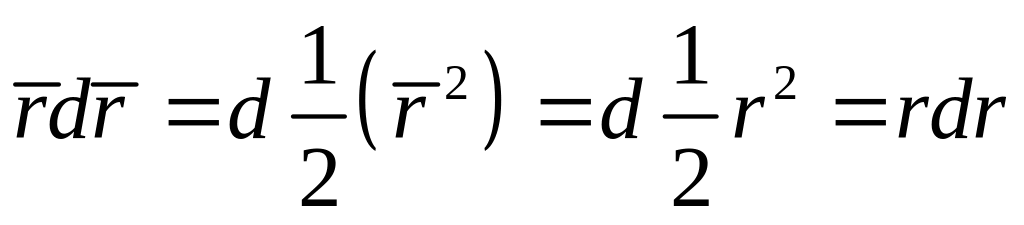. Интегрируем

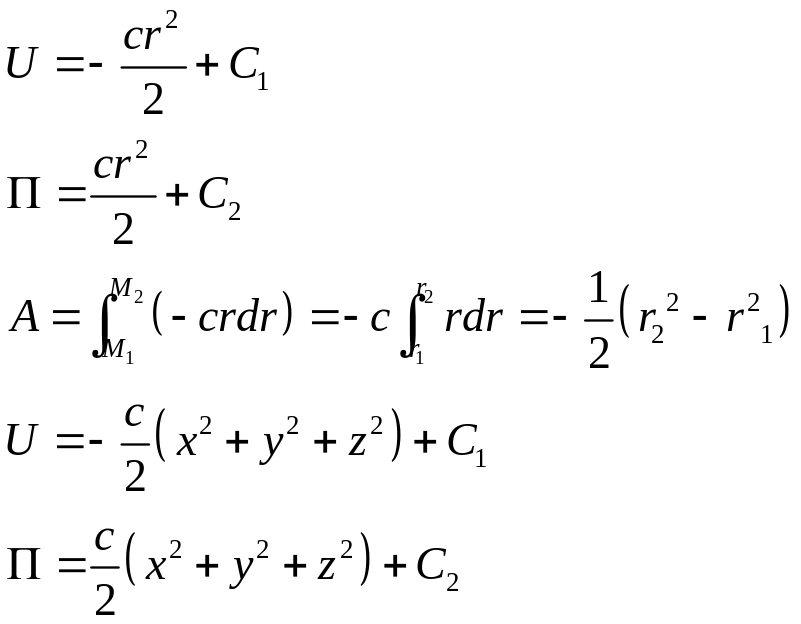
Таким образом, силовая функция и потенциальная энергия линейной силы упругости является квадратичной формой координат точки М, отсчитываемых от положения равновесия.

Работа силы упругости не зависит от траектории. При перемещении точки из положения равновесия работа силы упругости отрицательна

Поверхностями уровня линейной упругой силы будут концентрические сферы с центром в начале координат, а силовыми линиями – прямые, проходящие через начало координат, т.к. из

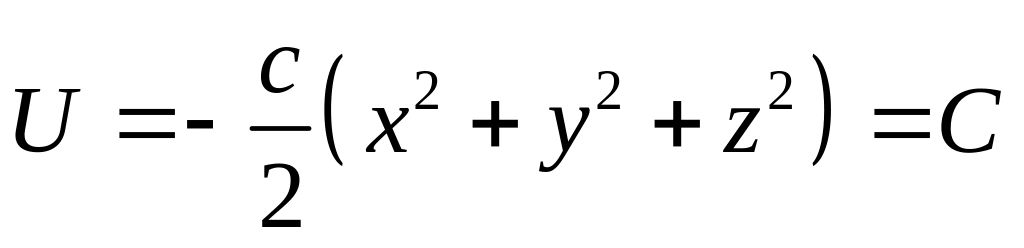
следует

25. Закон сохранения полной механической энергии системы.

Если все силы, действующие на систему, потенциальны, то при движении системы её полная механическая энергия постоянна

Пусть все силы, действующие на механическую систему, потенциальны, т.е. существует функция , такая, что

(I)

где - равнодействующая всех сил, приложенных к k-й точке.

Теорема об изм. кин. эн. в дифф. форме:

где . Согласно (I)

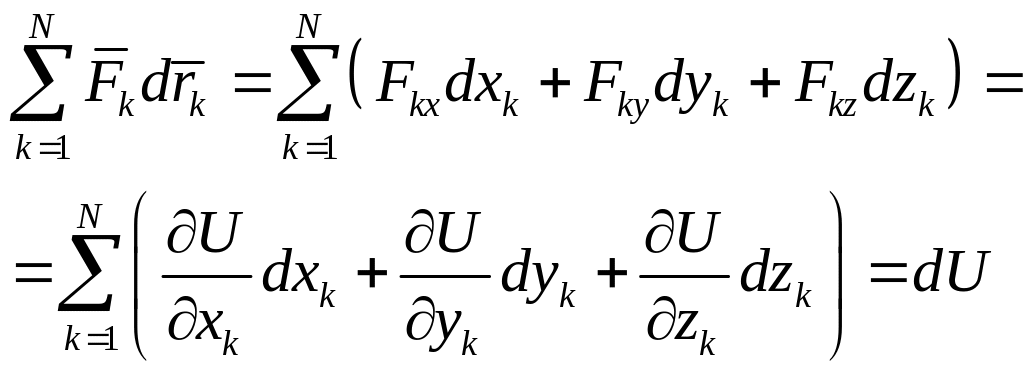
Таким образом

Или

Где - потенциальная энергия системы, следовательно,

отсюда

и

Сумма кинетической и потенциальной энергии называется полной энергией Е механической системы.

Системы, для которых выполняется закон сохранения механической энергии, называются консервативными.

26. Принцип Даламбера для точки и системы материальных точек.

При движении материальной точки в любой момент времени приложенные к ней активные силы и реакции связей вместе с силой инерции образуют систему сил, эквивалентную нулю (уравновешенную систему сил)

В соответствии с аксиомами статики основное уравнение движения материальной точки имеет вид

- равнодействующая активных сил, - равнодействующая реакций связей.

Запишем уравнение в виде

Слагаемое обозначают и называют даламберовой силой инерции (или просто силой инерции).

При движении механической системы в любой момент времени приложенные силы и реакции связей вместе с силами инерции образуют систему сил, эквивалентную нулю.

(I)

Суммируя левые части по всем точкам

Умножив каждое уравнение векторно слева на радиус-вектор k-й точки и просуммировав их, имеем:

или

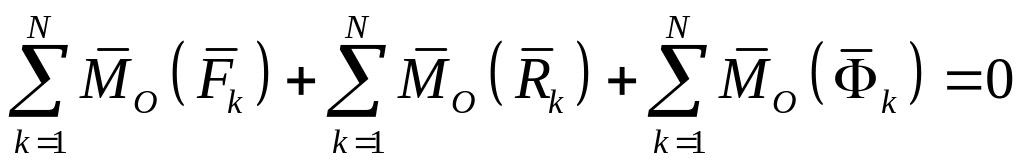
Если силы, приложенные к k-й точке системы, разложить на внешнюю и внутреннюю, а не на активные и реакции связей, то

Так как главный вектор и главный момент относительно произвольного центра приведения внутренних сил системы равен нулю, то