15. Теорема об изменении кинетического момента системы материальных точек в относительном движении по отношении к центру масс.

Первая производная по времени от главного момента количеств движения системы, вычисленного относительно центра масс для относительного движения механической системы по отношению к центру масс (по отношению к системе координат, движущейся поступательно вместе с центром масс), равна главному моменту внешних сил, действующих на точки системы, относительно центра масс.

Пусть подвижная система координат CXYZ связана с центром масс и движется поступательно относительно неподвижной системы Oxyz. Согласно теореме об изменении главного момента количеств движения системы относительно центра О для абсолютного движения механической системы,

с учётом и

Но как векторное произведение коллинеарных векторов. Используя теорему об изменении количества движения механической системы получаем

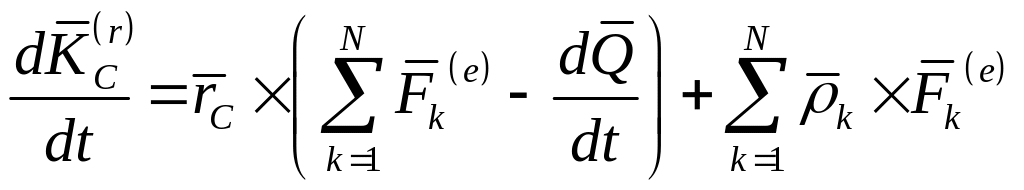
Окончательно имеем

16. Дифференциальные уравнения плоского движения твёрдого тела.

***

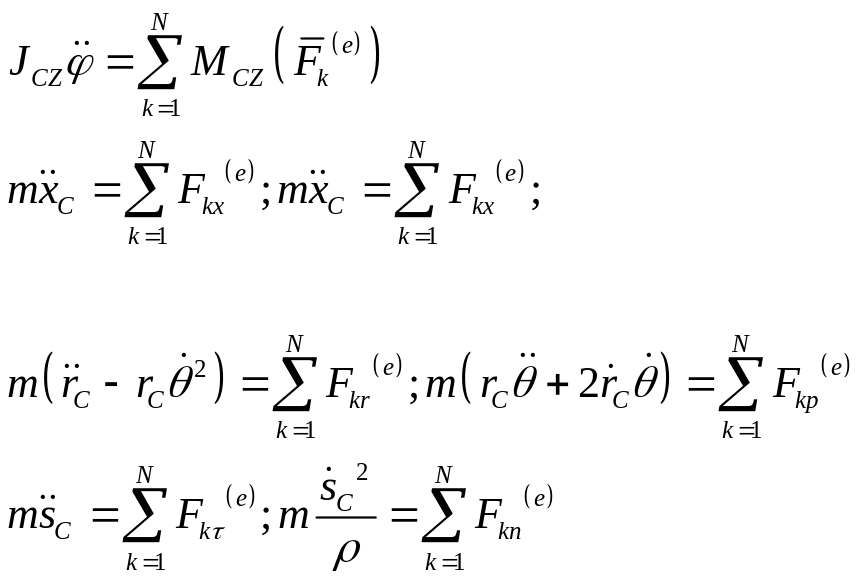
Дифф. уравнения плоского движения твёрдого тела получим на основании теорем о движении центра масс и об изменении главного момента количеств движения в относительном движении по отношению к центру масс.

В неподвижной системе Oxyz координат согласно для центра масс будем иметь

(I)

Введем подвижную СК CXYZ, имеющую начало в ЦМ тела и перемещающуюся относительно системы Oxyz поступательно, причем плоскости Oxy и CXY будем считать совпадающими с плоскостью, в которой движется ЦМ. Теорема об изменении момента количеств движения в относительном движении по отношению к ЦМ в проекции на CZ подвижной СК:

в уравнении главный момент количеств движения тела в его относительном вращении вокруг оси CZ подвижной СК

Следовательно, дифф. уравнение, описывающее вращение твёрдого тела относительно оси CZ, имеет вид

(II)

Эти два уравнения (I),(II) полностью описывают плоское движение твёрдого тела.

В проекциях на оси полярной СК:

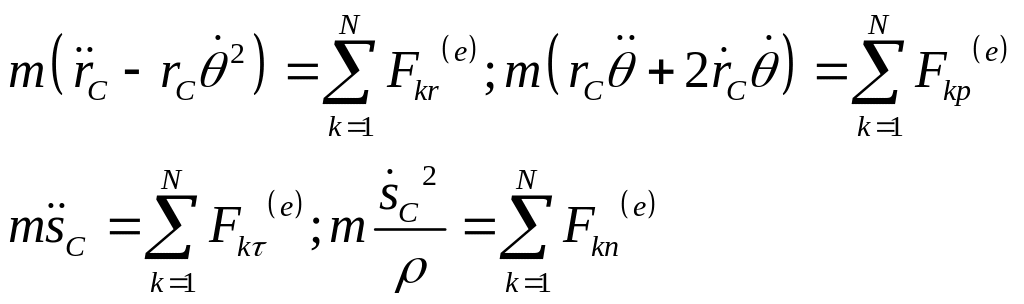
Где - полярные координаты центра масс тела в неподвижной системе отсчёта. - закон движения центра масс по траектории.

Начальные условия в общем случае:

При

или

или

В зависимости от числа степеней свободы тела для описания его плоского движения можно использовать от одной до трёх обобщенных координат, используемые в приведённых выше уравнениях и начальных условиях.

17. Элементарная и полная работа силы. Мощность. Работа равнодействующей силы.

Элементарная работа силы равна произведению элементарного перемещения на проекцию силы на это перемещение.

Элементарная работа силы равна скалярному произведению векторов силы и дифференциала радиус-вектора точки её приложения.

(I)

Элементарная работа силы равна скалярному произведению элементарного импульса на скорость точки её приложения.

Пусть точка приложения силы перемещается по криволинейной траектории из положения в положение . Разобьём перемещение точки М по дуге на элементарные бесконечно малые перемещения ds и определим работу силы на каждом таком перемещении

где - угол между векторами и в точке .

- выражение элементарной работы не всегда является полным дифференциалом.

Т.к. ,то

Поскольку

или

Так как

Можно представить (I) в виде

Полную работу силы на перемещении точки из положения в положение определяют как предел суммы её элементарных работ, т.е.

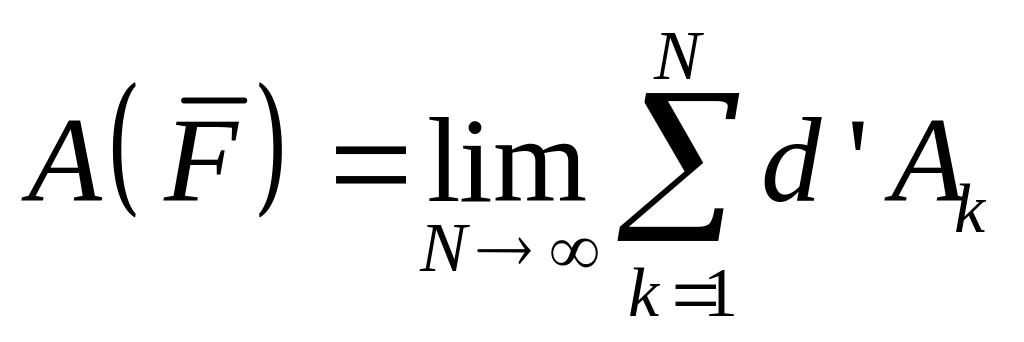
Так как сумма является интегральной суммой определения криволинейного интеграла, то

Или

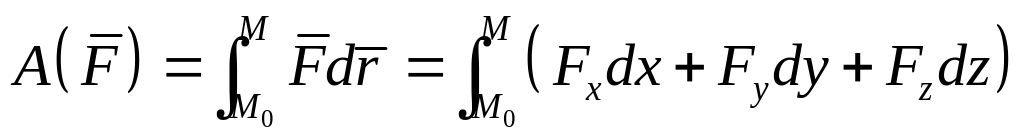
Если же сила является функцией времени (переменная сила) то работа силы на промежутке времени от 0 до t, соответствующем точкам и , определяется выражением

Работа силы зависит от характера движения точки приложения силы. Так, А = 0, если сила приложена к неподвижной точке или к точке, скорость которой во время движения равна нулю (например, МЦС)

Работа равнодействующей силы.

Рассмотрим систему сил, приложенную к рассматриваемой точке. Эта система имеет равнодействующую , причём

Тогда работа силы на перемещении точки из в текущее положение М равна алгебраической сумме работ составляющих сил на том же перемещении:

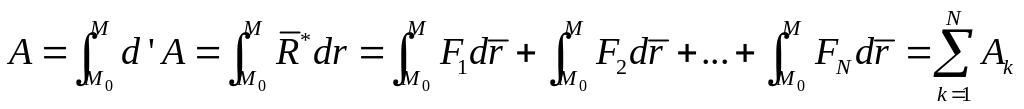
Мощнсть.

Отношение элементарной работы силы к промежутку времени, за которое оно произошло, называется мощностью.

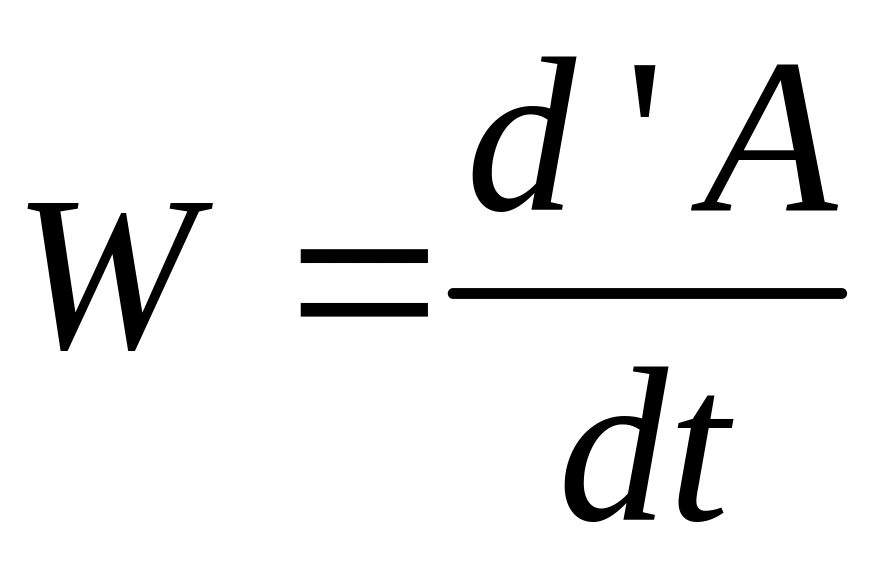
Так как то

Мощность силы равна скалярному произведению силы на скорость точки её приложения.