
- •II семестр
- •Аксимомы динамики. Инерциальная система отсчета.
- •Дифференциальные уравнения движения точки в векторной форме и в проекциях на декартовы и естественные оси координат.
- •Две основные задачи динамики точки. Интегралы уравнений движения.
- •Диф. Уравнения движения точки в неинерциальной системе отсчета.
- •Принцип относительности Галилея-Ньютона.
- •Центр масс системы материальных точек. Теорема о движении центра масс. Частные случаи.
- •2. Пусть теперь проекция главного вектора внешних сил, действующих на систему, на одну из осей (например, ось Ох) равна нулю , тогда из первого уравнения (6) следует , а значит
- •Теорема об изменении количества движения механической системы в дифференциальной и интегральной формах. Частные случаи.
- •Дифференциальные уравнения поступательного движения твердого тела.
- •Кинетический момент точки и системы материальных точек относительно центра и оси.
- •Теорема об изменении кинетического момента для точки и системы материальных точек. Законы сохранения кинетического момента.
- •Кинетический момент твёрдого тела относительно оси вращения.
- •Дифференциальные уравнения вращения тела вокруг неподвижной оси.
- •Движение точки под действием центральной силы, теорема площадей.
- •Кинетический момент системы материальных точек при сложном движении.
- •Теорема об изменении кинетического момента системы материальных точек в относительном движении по отношении к центру масс.
- •Дифференциальные уравнения плоского движения твёрдого тела.
- •Элементарная и полная работа силы. Мощность. Работа равнодействующей силы.
- •Работа сил, приложенных к твёрдому телу при его различных движениях.
- •Кинетическая энергия точки и системы материальных точек. Теорема Кенига.
- •Кинетическая энергия твёрдого тела в различных случаях его движения.
- •Теорема об изменении кинетической энергии для точки и системы материальных точек.
- •Потенциальное силовое поле. Силовая функция и потенциальная энергия поля.
- •Поверхности уровня и их свойства.
- •Примеры вычисления силовых функций однородного поля силы тяжести и линейной силы упругости.
- •Закон сохранения полной механической энергии системы.
- •Принцип Даламбера для точки и системы материальных точек.
- •Главный вектор и главный момент сил инерции в общем и частном случаях движения твёрдого тела.
- •Связи и их классификация.
- •Элементарная работа силы на возможном перемещении. Идеальные связи. Примеры.
- •Принцип возможных перемещений.
- •Общее уравнение динамики (механики)
- •Обобщенные силы. Способы вычисления обобщенных сил.
- •Условия равновесия механической системы, выраженные в обобщенных силах.
- •Вывод уравнений Лагранжа 2-го рода.
- •Момент инерции твёрдого тела относительно оси, проходящей через заданную точку в заданном направлении.
- •Эллипсоид инерции. Главные оси инерции симметричных твёрдых тел.
Теорема об изменении количества движения механической системы в дифференциальной и интегральной формах. Частные случаи.
Количеством
движения материальной точки М называют
вектор,
равный произведению массы m
точки на её скорость
![]()
![]()
Количеством
движения механической системы называют
вектор
![]() ,
равный геометрической сумме количеств
движения точек системы:
,
равный геометрической сумме количеств
движения точек системы:

Вектор называют также главным вектором количеств движения точек материальной системы.
![]()
Элементарным
импульсом силы
![]() ,
действующей в течении времени dt,
,
действующей в течении времени dt,
![]()
Теорема в дифференциальной форме.
Первая производная по времени от вектора количества движения механической системы равна главному вектору внешних сил, действующих на материальные точки этой системы.
|
Запишем теорему о движении центра масс механической системы в виде

Окончательно имеем:
(7)
Получим отсюда еще одну дифф. форму теоремы
 (8)
(8)
Таким образом, дифференциал количества движения механической системы равен сумме элементарных импульсов внешних сил, действующих на материальные точки системы.
Теорема в интегральной форме
Изменение количества движения системы за время t равно векторной сумме полных импульсов внешних сил, действующих на точки механической системы за то же время.
|
Проинтегрируем (8) по времени в пределах от 0 до t и поменяем местами операции интегрирования и суммирования:

![]() - соответственно
количества движения мех. системы в
произвольный и начальный моменты
времени.
- соответственно
количества движения мех. системы в
произвольный и начальный моменты
времени.
![]() - полный импульс внешней силы, действующей
на k-ю
материальную точку.
- полный импульс внешней силы, действующей
на k-ю
материальную точку.
Дифференциальные уравнения поступательного движения твердого тела.
При поступательном
движении тела его угловая скорость, а
следовательно и главный момент количеств
движения относительно центра масс
тождественно равны нулю. На основании
теоремы о движении центра масс механической
системы, уравнение
![]() применительно
к рассматриваемому случаю имеет вид
применительно
к рассматриваемому случаю имеет вид

Запишем его в виде векторного дифференциального уравнения поступательного движения твёрдого тела.

В проекциях на декартовы оси координат:

В общем случае поступательного движения тело имеет три степени свободы и его движение можно задать, определив движение центра масс тела в декартовой системе координат.
В проекциях на естественные оси координат:

Кинетический момент точки и системы материальных точек относительно центра и оси.
Моментом количества движения материальной точки (кинетическим моментом) массой m относительно центра О называют векторную величину, равную векторному произведению радиус-вектора материальной точки, проведённого из этого центра, на количество движения точки:
![]()
Так как

то моменты количества движения материальной точки относительно осей координат имеют вид
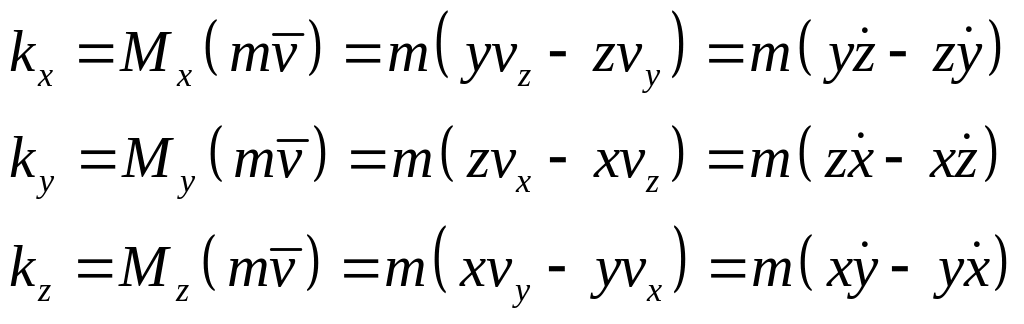
Теорема об изменении кинетического момента для точки и системы материальных точек. Законы сохранения кинетического момента.
Первая производная по времени от момента количества движения точки относительно центра О равна моменту равнодействующей силы относительно того же центра О.
|
Уравнение движения мат. точки::

умножим его векторно слева на радиус-вектор

Преобразуем левую часть полученного уравнения
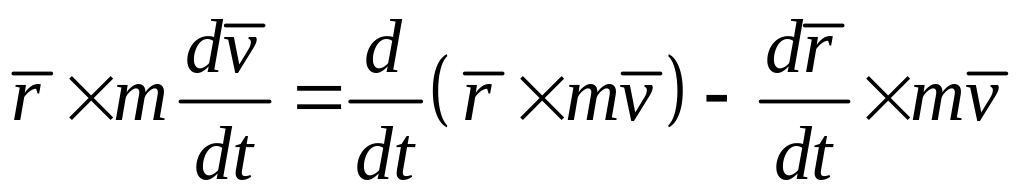
Но
 как
векторное произведение коллинеарных
векторов.
как
векторное произведение коллинеарных
векторов.

Первая производная по времени от главного момента количеств движения механической системы относительно неподвижного центра О равна главному моменту внешних сил, приложенных к точкам системы, относительно того же центра.
|
Рассмотрим мех.
систему
![]() из N
материальных точек, к каждой из которых
приложены равнодействующие внешних и
внутренних сил. Для каждой точки
из N
материальных точек, к каждой из которых
приложены равнодействующие внешних и
внутренних сил. Для каждой точки
![]() запишем
теорему об изменении момента количества
движения относительно неподвижного
центра О.
запишем
теорему об изменении момента количества
движения относительно неподвижного
центра О.

Просуммировав по всем точкам

и преобразовав левую часть уравнения получим:

Здесь
 - главный момент количеств движения
механической системы относительно
центра О.
- главный момент количеств движения
механической системы относительно
центра О.
Главный момент внутренних сил

а главный момент внешних сил

Окончательно имеем: (9)
Законы сохранения:
1. Закон сохранения главного момента количеств движения механической системы относительно центра О в векторной форме:
Если главный момент внешних сил относительно неподвижного центра О равен нулю, то главный момент количеств движения механической системы относительно этого центра постоянен по модулю и направлению.
|
Пусть главный
момент внешних сил системы относительно
центра О равен нулю, т.е.
![]() .
Тогда, согласно (9)
.
Тогда, согласно (9)

Интегрируя, получаем
2. Если главный момент внешних сил, действующих на механическую систему, относительно какой-либо оси равен нулю, то главный момент количеств движения механической системы относительно этой оси постоянен.
|
Пусть сумма внешних
моментов внешних сил, действующих на
механическую систему, относительно оси
Ох
равна нулю, т.е.
![]() .
Тогда
.
Тогда
Если рассматривается
тело или система тел, вращающихся вокруг
неподвижной оси Оz
с угловой скоростью
![]() и
и
![]() ,
то
,
то
![]() .
.



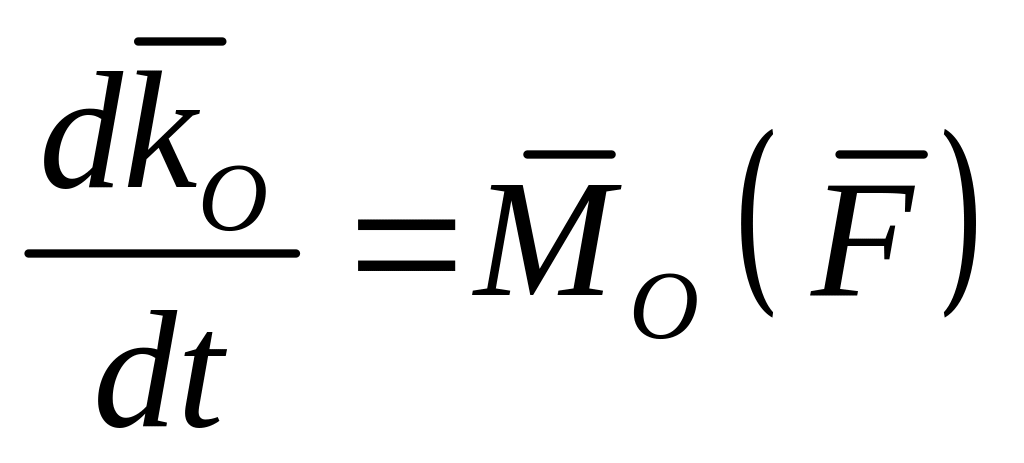
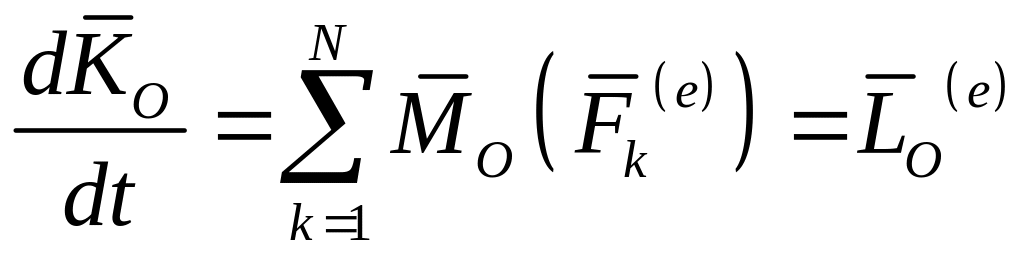 (9)
(9)