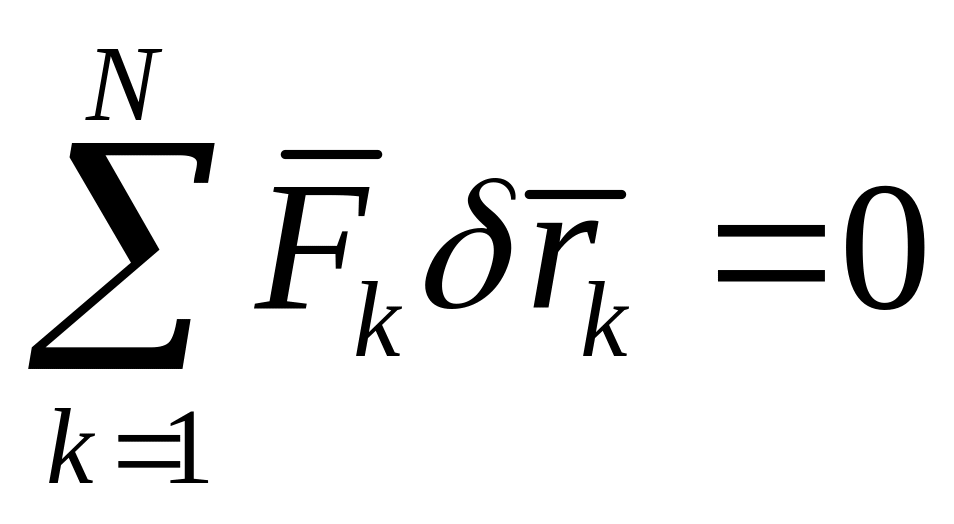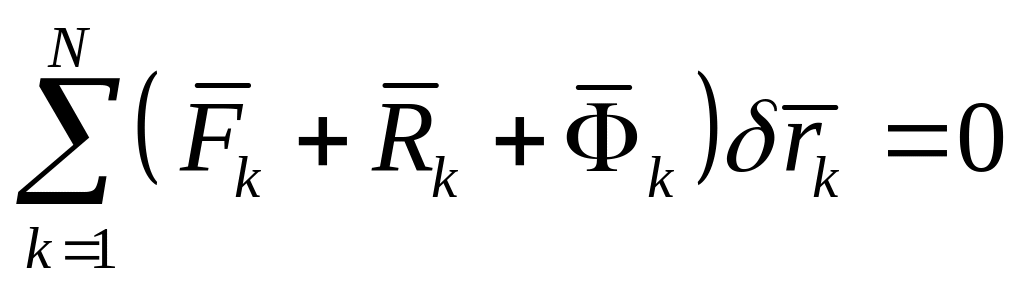30. Принцип возможных перемещений.

Чтобы данное положение механической системы со стационарными идеальными связями было положением равновесия, необходимо и достаточно, чтобы сумма элементарных работ активных сил на любом возможном перемещении системы из этого положения была равна нулю.

Положением равновесия называется такое положение механической системы, в котором она может находится сколь угодно долго, если в начальный момент времени система была приведена в это положение с нулевыми скоростями.

Необходимость.

Пусть мех. система из N материальных точек находится в равновесии. Тогда приложенные к каждой точке активные силы и реакции связей уравновешены, т.е.

Умножив каждое равенство на возможное перемещение соответствующей k-й точки и просуммировав скалярное произведение

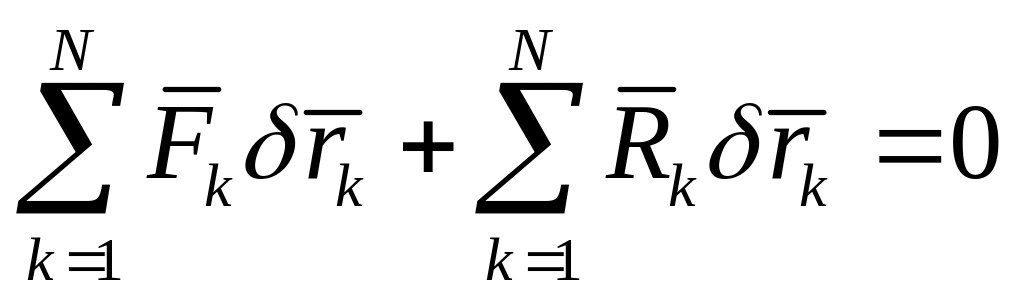
Если наложенные на систему связи идеальные, то и условие является необходимым условием равновесия системы.

Достаточность.

Предположим, что , а система не находится в равновесии. Значит под действием активных сил и реакций связей система за малый промежуток времени совершит некоторое действительное перемещение. При стационарных связях это действительное перемещение совпадает с одним из возможных, поэтому

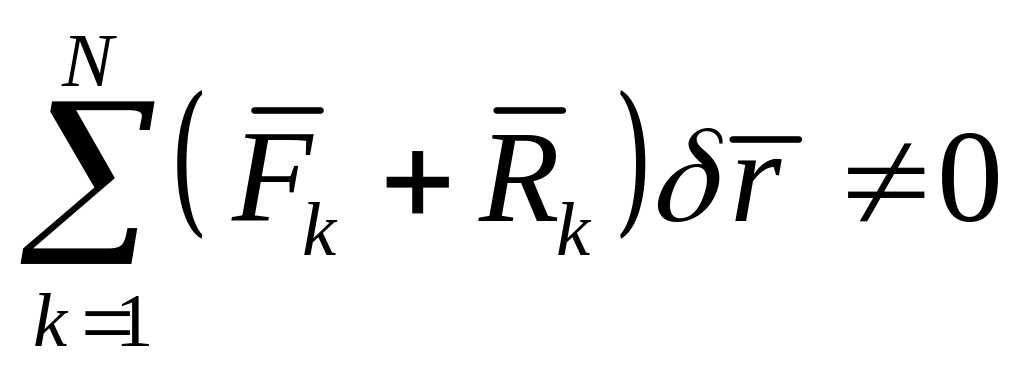
Так как связи идеальные, то и тогда 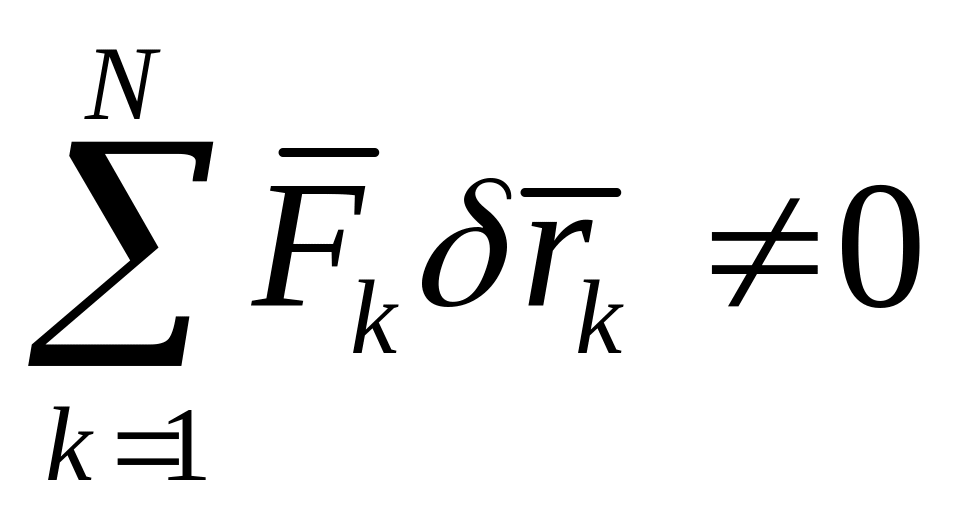, что противоречит принятому выше предположению.

31. Общее уравнение динамики (механики)

Общее уравнение динамики

Принцип Даламбера-Лагранжа

При движении механической системы в любой момент времени сумма работ активных сил, сил реакций связей и сил инерции на любом возможном перемещении из занимаемого положения равна нулю.

Рассмотрим систему из N мат. точек. В соответствии с принципом Даламбера, приложенные к каждой точке активные силы, реакции связей и силы инерции в любой момент времени образуют уравновешенную систему сходящихся сил. Эта система удовлетворяет условию равновесия

Умножим обе части уравнения на возможное перемещение k-й точки и просуммируем полученные для всех точек системы произведения.

Раскрывая скалярные произведения получаем

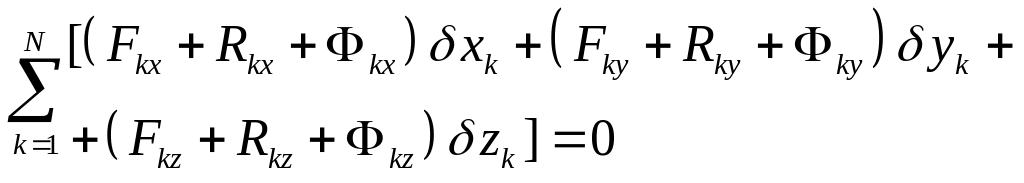
Или

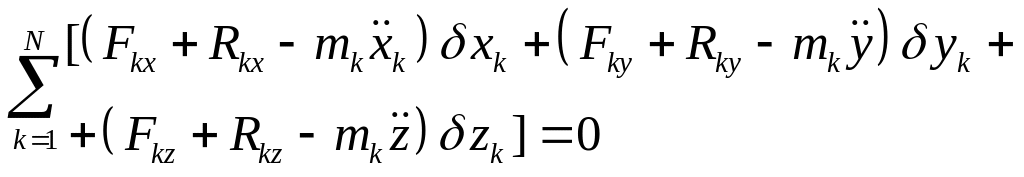
Если связи, наложенные на систему, идеальные, то и

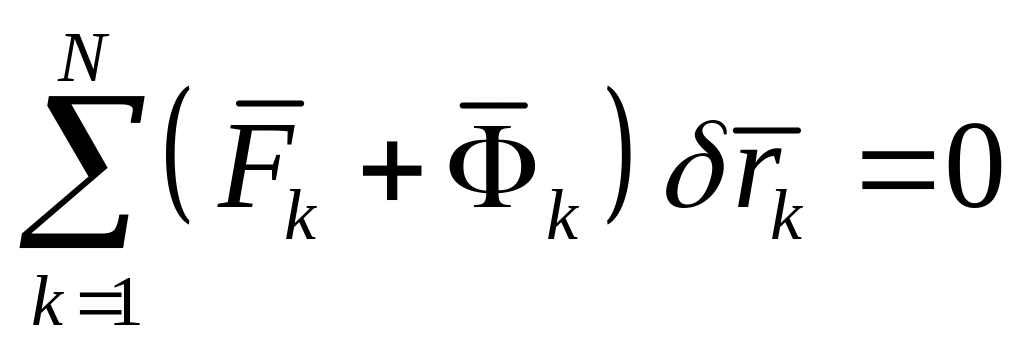
В обобщенных координатах

Общее уравнение динамики в обобщенных силах

32. Обобщенные силы. Способы вычисления обобщенных сил.

Обобщенной силой, соответствующей i-й обобщенной координате, называется величина, равная коэффициенту при вариации данной обобщенной координаты в выражении возможной работы сил, действующих на механическую систему.

Рассмотрим возможную работу сил, приложенных к точкам системы

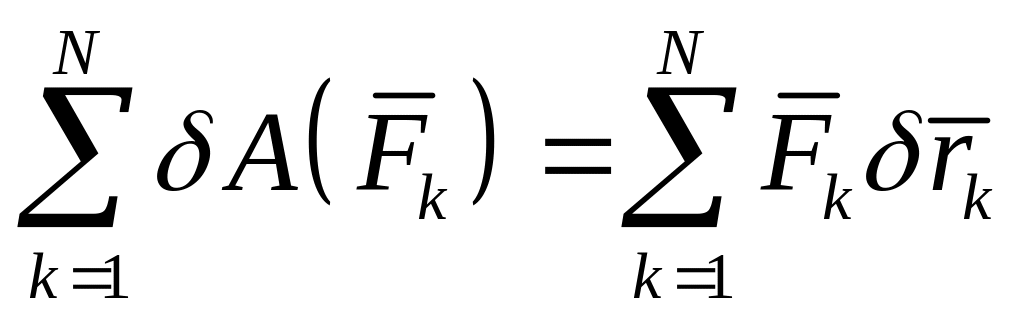
Если мех. система при наложенных на неё голономных удерживающих связях имеет n степеней свободы, то положение этой системы определяется обобщенными координатами и . Возможное перемещение k-й точки

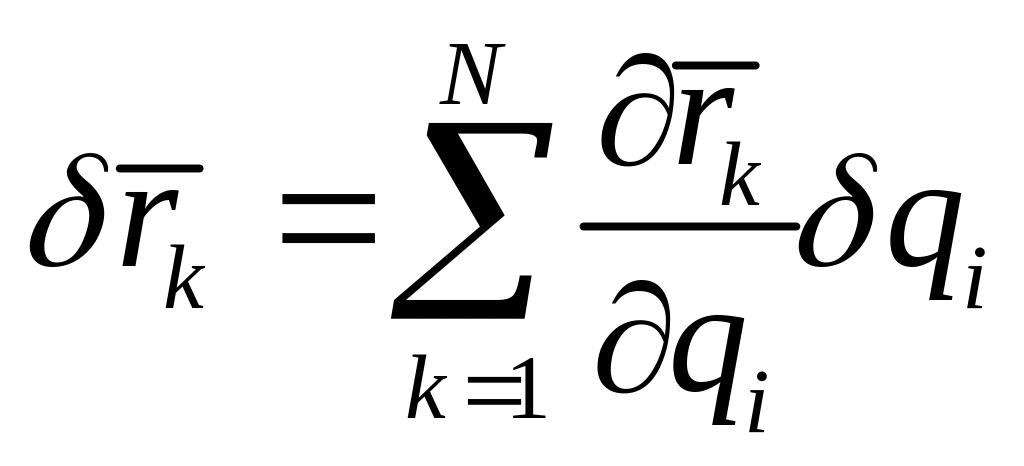
Подставляя в формулу для возможной работы сил, получаем

Способы вычисления

- согласно определению, обобщенная сила

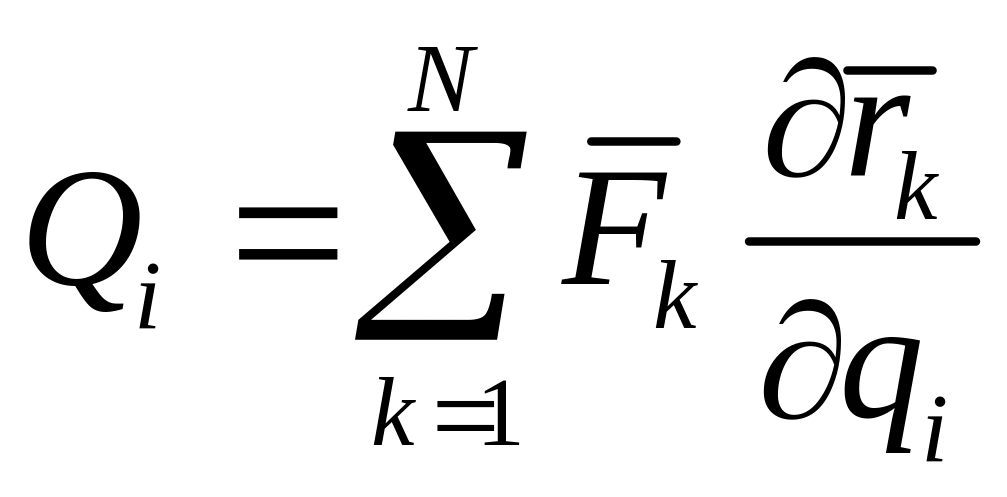
Принимая во внимание, что ,

получаем

Этот способ называют аналитическим.

- Обобщенные силы для механических систем с n>1 целесообразно вычислять последовательно, учитывая, что обобщенные координаты, а значит, и их вариации независимы между собой. Системе всегда можно сообщить такое возможное перемещение, при котором изменяется только одна обобщенная координат, а другие при этом не варьируются. В этом случае

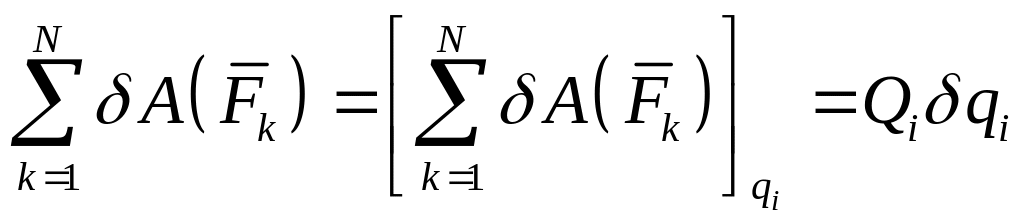
откуда