
- •Оглавление
- •Лекция 5 Шлицевые и профильные соединения 48
- •Введение
- •Лекция 1 основные критерии работоспособности при расчетедеталей машин.
- •1.7 Снижение массы машин (металлоемкость) по агротехническим требованиям
- •2 Расчетные нагрузки
- •3 Пути повышения надежности деталей машин на стадии проектирования
- •Лекция 2
- •2 Заклепочные соединения и их расчет
- •2.1 Общие сведения.
- •2.2 Основные типы заклепок и конструкций швов (Рис.5)
- •2.3 Расчет заклепочных швов
- •Расчет заклепочных соединений на срез;
- •3 Соединения деталей с натягом и их расчет
- •3.1 Общий сведения
- •3.2 Определение прочности соединения
- •3.3 Определение усилия запрессовки
- •3.4 Определение температуры нагрева
- •1 Сварные соединения и их расчет
- •2 Клеевые соединения и их расчет
- •1.2 Основные типы сварных соединений
- •1.3 Расчет сварных соединений
- •3 Клеевые соединения и их расчет
- •Рие.26 Типы клеевых швов: 1 - нахлесточный; 2 -стыковые
- •Расчет на срез:
- •Расчет на смятие
- •Лекция 4 шпоночные соединения и их расчет
- •2 Расчет шпоночных соединений
- •2.1 Расчет призматических шпонок
- •Расчет сегментных шпонок
- •2.3 Конструкция соединения с цилиндрической шпонкой (штифтом)
- •2.4 Клиновые шпонки
- •2.5 Тангенциальные шпонки
- •2.6 Фрикционные шпонки
- •3 Материал шпонок и допускаемые напряжения
- •Лекция 5 шлицевые и профильные соединения
- •1 Назначение, область применения и основные типы шлицевых соединений
- •2 Расчет шлицевых соединений
- •3 Профильные (бесшлицевые) соединения
- •1 Назначение, область применения и основные типы шлицевых соединений
- •2 Расчет шлицевых соединений
- •2 Профильные (бесшлицевые) соединения
- •Лекция 6 резьбовые соединения
- •1 Назначение и область применения резьбовых соединений
- •2 Образование резьбы и ее параметры
- •3.5 По назначению:
- •4 Расчетные формулы для резьбовых соединений
- •Основные причины выхода деталей резьбовых соединений.
- •Различные случаи расчета резьбовых соединений,
- •1 Основные причины выхода деталей резьбовых соединений,
- •2 Различные случаи расчета резьбовых соединений
- •2.1 Расчет резьбы винта и гайки на смятие и срез ( Рис.41):
- •2.2 Расчет винтов, нагруженных только осевой силой без начальной затяжки.
- •2.3 Расчет винтов, нагруженных осевой нагрузкой и предварительным моментом затяжки
- •2.4 Расчет резьбовых соединений нагруженных силами в плоскости стыка
- •2) Расчет болтов, установленных без зазора ведут на срез.
- •2.5 Расчет резьбовых соединений, включающих группу болтов
- •2.6 Расчет винтов клеммовых соединений
- •2 Особенности работы механических приводов сельхозмашин
- •3 Характеристики механических передач
- •4 Кинематический расчет механического привода
- •Подшипниках
- •2 Эвольвента и эвольвентное зацепление. Геометрические соотношения в эвольвентном зубчатом зацеплении
- •3 Основные параметры зубчатых передач
- •4 Причины неисправности зубчатых колес
- •Расчёт цилиндрической прямозубой передачи
- •Расчет прямозубых колес по напряжениям изгиба
- •Допускаемые напряжения изгиба
- •3 Силы, действующие в прямозубой передаче, и давление на опоры
- •Лекция 11 Цилиндрические зубчатые колеса с косыми и шевронными зубьями
- •2 Расчет косозубых колес по контактным напряжениям и напряжениям изгиба
- •2.1 Общие сведения
- •Так как делительные диаметры
- •Расчет зубьев косозубых колес по контактным напряжениям Для эквивалентного прямозубого колеса.
- •Расчет косозубых колес по напряжениям изгиба
- •Шевронные зубчатые колеса и их расчет
- •Напряжений
- •Порядок расчета зубчатой передачи с цилиндрическими колесами
- •1 Проектный расчет закрытой передачи
- •Расчет первой ступени рекомендуется вести в такой последовательности:
- •Контактные напряжения зубьев шестерни
- •Напряжение изгиба зубьев шестерни
- •2. Проектный расчет открытой передачи
- •Напряжения изгиба в зубьях шестерни
- •3 Силы, действующие в косозубой передаче и давления на опоры.
- •Лекция 12 онические зубчатые передачи.
- •Назначение, область применения.
- •2 Условные и геометрические соотношения (обозначения) в конических колесах.
- •Основные параметры конических зубчатых передач.
- •2 Ширина венца зубчатых колес “b” в закрытых передачах
- •Лекция 13 Расчет конической зубчатой передачи
- •Расчет зубьев конической передачи на выносливость по контактным напряжениям
- •1.3 Расчет зубьев на выносливость по напряжениям изгиба
- •2 Силы, действующие в зубчатых конических передачах
- •2.Условные обозначения
- •2.1 Условные обозначения (рис. 76, 77).
- •Основные параметры червячных передач
- •Коэффициент диаметра червяка.
- •Межосевое расстояние червячной передачи без смещения
- •6 Кпд червячной передачи
- •4 Силы, действующие в червячном зацеплении
- •Лекция 15 Расчет червячной передачи
- •1 Основные причины выхода из строя червячных передач
- •2.2. Расчет червячного колеса по контактным напряжениям
- •2.3 Расчет червячного колеса по напряжениям изгиба
- •3. Расчет червяка на прочность и жесткость.
- •4 Червячные редукторы, применяемые в сельском хозяйстве
- •5 Тепловой расчет червячного редуктора
- •Брызговик; 2- крыльчатка; 3- ребра.
- •Лекция 16 зубчатое зацепление м. Л. Новикова, планетарные и волновые передачи
- •Расчет на прочность
- •Планетарные передачи
- •Назначение, область применения, достоинства и недостатки.
- •2.2 Передаточное число
- •2.3 Разновидность планетарных передач
- •2.5 Выбор числа зубьев
- •3 Волновые передачи
- •3.1 Общие сведения
- •3.2 Передаточное число
- •3.3 Расчет волновых передач
- •Лекция 17 цепные передачи
- •Назначение и область применения.
- •Основные характеристики цепных передач.
- •Расчет цепных передач.
- •1 Назначение и область применения
- •2 Основные характеристики цепных передач
- •2.1 Основные геометрические характеристики цепи
- •2.2 Передаточное число передачи
- •2.3 Средняя скорость цепи
- •2.4 Межосевое расстояние для втулочной цепи
- •2.5 Число звеньев цепи z3
- •2.6 Силы, действующие в ветвях цепи
- •2.7 Нагрузка на валы
- •3 Расчет цепных передач
- •3.1Основной критерий работоспособности приводных цепей
- •3.2. Расчет цепной передачи
- •Лекция 18 фрикционные передачи и вариаторы
- •1 Назначение, область применения фрикционных передач
- •2 Основные типы фрикционных передач
- •3 Расчет фрикционных передач
- •1 Назначение, область применения фрикционных передач
- •2 Основные типы фрикционных передач
- •2.2 Конусная фрикционная передача
- •2.3Лобовой вариатор
- •2.4 Вариатор с раздвижными конусами
- •2.5 Торовый вариатор
- •2.6 Дисковые выриаторы
- •3 Основы расчета прочности фрикционных пар
- •Ременная передача и ее расчет
- •1 Назначение, область применения, типы ременных передач, материал и конструкция ремней
- •2 Порядок расчета ременной передачи
- •1 Назначение, область применения, типы ременных передач, материал и конструкция ремней
- •1.2 Материал и конструкция ремней
- •2 Расчет ременной передачи
- •2.1 Окружная скорость ведущего и ведомого шкивов:
- •2.2 Передаточное число
- •2.3 Окружная сила
- •2.4 Начальная сила натяжения ремня
- •2.5 Силы натяжения
- •2.6 Сила давления на вал
- •2.7 Диаметр меньшего шкива плоскоременной передачи:
- •2.8 Угол обхвата ремнем меньшего шкива
- •2.9 Межосевое расстояние ременной передачи
- •2.10 Расчетная длина ремней
- •2.11 Расчет ремней.
- •2.12 Расчет клинового ремня
- •2.13 Расчет ремней долговечность
- •2.14 Порядок расчета ременной передачи:
- •2.15 Расчет ременной передачи
- •Решение
- •2.16.Расчет клиноременной передачи
- •Лекция 20
- •Назначение, конструкция и материалы
- •Расчет валов и осей
- •1 Назначение конструкция и материалы
- •1.2 Валы
- •1.3 Некоторые требования к конструкции валов
- •1.4 Материал осей и валов
- •2 Расчёт осей и валов
- •2.1 Расчет осей и валов на прочность
- •2.2 Расчет валов и осей на сопротивление усталости
- •2.3 Расчет валов на жесткость
- •Лекция 21 подшипники скольжения
- •Назначение, конструкция, материалы
- •Расчет подшипников скольжения
- •1 Назначение, конструкция, материалы
- •1.1 Назначение подшипников скольжения
- •1.2 Смазка подшипников скольжения
- •2 Расчет подшипников скольжения.
- •2.1 Расчет подшипников скольжения с полусухим или полужидкостным трением.
- •2.2 Расчет подшипников скольжения с жидкостным трением.
- •Лекция 22
- •2 Типы подшипников
- •3 Расчет подшипников и выбор их по госту
- •4 Установка, монтаж, смазка и уплотнение подшипника качения
- •4.1 Поля допусков валов и отверстий корпусов для установки подшипников качения
- •4.2 Монтаж и демонтаж подшипников качения:
- •4.3 Смазка подшипников
- •4.4 Уплотнение подшипников
- •Лекция 23
- •Назначение, область применения, классификация, типы муфт
- •Расчет муфт
- •1 Назначение, область применения, классификация, типы муфт
- •1.1 Назначение и область применения муфт
- •1.2 Классификация и типы муфт
- •1.3 Типы муфт
- •2 Расчет муфт
- •2.1 Расчетный момент
- •Расчет неуправляемых муфт
- •2.4 Расчет зубчатых муфт
- •2.5 Расчет муфт типа мувп
- •2.6 Расчет муфт со срезаемым штифтом
- •Назначение, конструкция и материалы
- •Расчет винтовых цилиндрических пружин
- •1 Назначение, конструкция и материалы
- •2 Расчет винтовых цилиндрических пружин растяжения и сжатия.
- •2 Основные правила проектирования
- •2.1 Связь проектирования с технологией изготовления
- •2.2 Связь проектирования с обработкой на станках
- •2.3 Выбор допусков и посадок
- •2.4 Выбор шероховатостей деталей машин и обозначение ее на чертежах
- •2.5 Выбор материала деталей
- •2.6 Нанесение на чертежах показателей свойств материалов.
- •2.7 Техника расчета.
- •2.8 Оформление чертежей
- •3 Методика расчета приводов машин
- •Лекция 26
- •1 Этапы разработки новой техники
- •2 Анализ понятий проектирование и конструирование
- •3 Техническое задание и его анализ
- •3.1 Информационный поиск.
- •3.2 Проектные стадии разработки.
- •4 Ошибки в разработках новых изделий и борьба с ними
- •5 Конструирование и проектирование деталей машин с применением компьютера,
- •Приложение Краткое методическое указание к изучению материала
2 Расчет ременной передачи
Сила натяжения ведущей ветви ремня F1, сбегающей с ведомого шкива во время работы передачи, больше силы натяжения ведомой ветви его F2, набегающей на ведомый шкив. Из диаграммы (эпюры) сил, возникающих в поперечном сечении ремня (Рис. 115,116).
Теория упругости скольжения ремня на шкивах разработана профессорами Н.И. Петровым и H.Б. Жуковским. По этой теории изменения сил натяжений происходит на дугах упругого скольжения, соответствующих углам β1 β2, которые меньше углов α1 α2 обхватов шкива ремнем.
Относительное скольжение ремня равно разности относительных удлинений ведущей ε1 и ведомой ε2 ветвей: ε = ε1 – ε2.
2.1 Окружная скорость ведущего и ведомого шкивов:
Вследствие упругого скольжения ремня на шкивах:
![]()
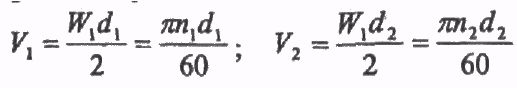 .
(289)
.
(289)
2.2 Передаточное число
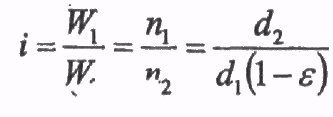 .
(290)
.
(290)
Величина относительного скольжения: ε = 0,01…0,02 (от типа ремня).
Так
как величина ε
мала, то можно пользоваться формулами:
![]() .
Передаточное
число ремня в большинстве случаев
принимается: U≤4.
.
Передаточное
число ремня в большинстве случаев
принимается: U≤4.
2.3 Окружная сила
Окружную силу на ведущем колесе, шкиве определяют по формуле:
![]()
где Ft – окружная сила, Н;
N – мощность, Вт;
V – скорость, м/с;
Kg – коэффициент динамической нагрузки и режима работы передачи;
Kg = 1,1…1,6 (берётся по таблице)
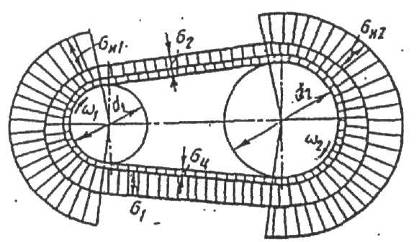
Рис 115 Напряжения в ремне работающей передачи
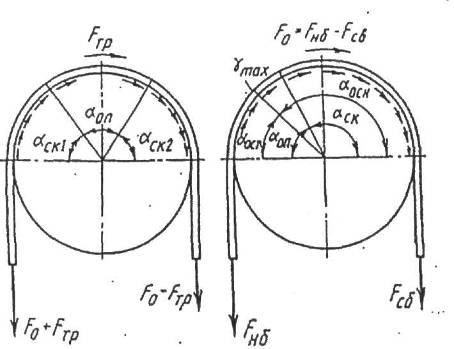
Рис 116 Взаимодействие ремня со шкивом
2.4 Начальная сила натяжения ремня
Начальную силу натяжения ремня (предварительное натяжения) принимают такой, чтобы ремень мог сохранить это натяжение достаточно длительное время, не подвергаясь большой вытяжке и не теряя требуемой долговечности. Соответственно этому начальное напряжение в ремне для плоских стандартных ремней без автоматических нат. устройств:
σ0 =1,8 Н/мм², с автоматическим нат. устройством σ0 =2 Н/мм², для клиновых стандартных ремней σ0 =(1,2. . .1,5) Н/мм².
Тогда начальная сила натяжения ремня: F0 = Aσ0
Где А – площадь поперечного сечения ремня плоскоремённой передачи, мм. Площадь поперечного сечения всех ремней клиноремённой передачи, Z×А=ΣА.
2.5 Силы натяжения
Силы
натяжения ведущей и ведомой ветвей
ремня в нагруженной передаче можно
определить из условия равновесия
шкива:![]() ,
от куда F1
– F2
= Ft
,
от куда F1
– F2
= Ft
Так как сумма сил натяжений ремня постоянна, независимо от того, нагружена передача или нет, то: F1 + F2 = 2F0 (292)
Из вышесказанных выражений следует:
F1 = F0 + 0,5Ft; F2 = F0 + 0,5Ft (293)
Помимо рассмотренного способа определения сила ветвях ремня при работе передачи существует способ, основанный на рассмотрении условий равновесия гибкой нерастяжимой нити.
2.6 Сила давления на вал
Сила давления Q на вал шкива равна геометрической сумме сил натяжений ветвей ремня (Рис. 117,118,119,120).
Из параллелограмма следует (Рис. 120):
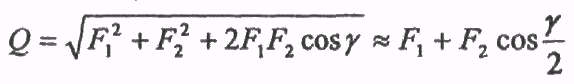 ,
(294)
,
(294)
где γ - угол между двумя ветвями ремня, град
Из
рис. 120 видно, что: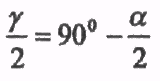 ,
,
где α - угол меньшего шкива.
Заменив
γ
через и приняв![]() получим:
получим:
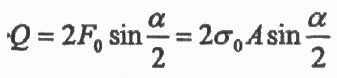 (295)
(295)
КПД при нормальных условиях работы в среднем для плоскоременных передач η=0,96, а для клиноременных передач η=0,95.
