1.3.3. Классификация видов деформирования

Внутренние силовые факторы имеют ярко выраженный физический смысл. Каждому из них соответствует определенный вид деформирования.

Если в поперечном сечении бруса возникает только нормальная сила (N≠0), то в зависимости от направления этой силы деформирование называют растяжением или сжатием.

Если в поперечном сечении бруса действует только крутящий момент (Мк≠0), то деформирование называют кручением.

Если в поперечном сечении бруса возникает только изгибающий момент (Мх≠0 или Му≠0), то деформирование называют чистым изгибом.

Если в поперечном сечении бруса возникает только поперечная сила (Qy≠0 или Q_x≠0), то деформирование называют сдвигом (срезом).

Перечисленные четыре вида деформирования (сопротивления) называют простыми, всякое их сочетание называют сложным деформированием (сложным сопротивлением).

1.3.4. Напряжения

В дальнейшем рассматривается механическое напряжение. Внутренние силы распределены по сечению бруса в общем случае неравномерно. Обратимся вновь к рассмотрению правой отсеченной части бруса, площадь поперечного сечения которого равна (рис. 1.3). Выделим в этом сечении в окрестности некоторой произвольной точки К достаточно малую площадку и обозначим равнодействующую внутренних сил, передаваемых через эту площадку, через . Отношение называют полным средним напряжением на рассматриваемой площадке. Для определения истинного полного напряжения в точке необходимо контур площадки стянуть к этой точке, то есть осуществить предельный переход при . Этот переход возможен, так как согласно гипотезе сплошности материала внутренние силы распределены непрерывно по всему сечению.

Р ис. 1.3

Вектор (1.2)

называется полным напряжением в рассматриваемой точке сечения. Произвольно ориентированный в пространстве вектор полного напряжения для удобства использования в расчетах обычно раскладывают на составляющие (см. рис. 1.3). Проекцию этого вектора на нормаль к площадке обозначают и называют нормальным напряжением. Проекцию на плоскость сечения обозначают τ и называют касательным напряжением. Касательное напряжение τ в свою очередь раскладывают по двум взаимно перпендикулярным направлениям в плоскости площадки и получают и .

Разложение полного напряжения на нормальное и касательное имеет определенный физический смысл. Нормальные силы, мерой интенсивности которых является , стремятся сблизить или отдалить частицы материала друг от друга, что может привести к разрушению тела в результате отрыва частиц. Касательные внутренние силы, мерой интенсивности которых является τ, вызывают сдвиг частиц материала друг относительно друга, что может привести к разрушению тела в результате взаимного сдвига частиц. Как следует из (1.2), напряжение - это интенсивность внутренних сил, то есть величина внутренних сил взаимодействия, приходящихся на единицу площади, выделенной в окрестности рассматриваемой точки. Единицей измерения напряжения является Паскаль . Так как Паскаль - очень малая величина, то в практических расчетах обычно используют более крупную величину – мегапаскаль . В дальнейшем предполагается, что в теле, свободном от нагрузок, напряжений нет, то есть используется так называемая гипотеза естественной ненапряженности.

1.4. Перемещения и деформации

1.4.1. Перемещения

Рассмотрим тело, на которое наложены связи таким образом, что перемещения этого тела как жесткого целого исключены (рис. 1.4). Такие тела называют кинематически (геометрически) неизменяемыми, и перемещения отдельных точек и сечений такого тела определяются только его деформацией. В дальнейшем рассматриваются только такие системы. Рассмотрим в недеформированном теле некоторую произвольную точку (частицу) А. В результате действия на тело уравновешенной системы внешних сил оно продеформируется, положение этой точки изменится, и она переместится в положение А₁. Вектор S, имеющий начало в точке недеформированного тела, а конец в этой же точке деформированного тела, называется вектором полного линейного перемещения этой точки (частицы). Проекции полного линейного перемещения на координатные оси x, y, z называются линейными перемещениями точки по осям и обозначаются через , и (см. рис. 1.4) или , и .

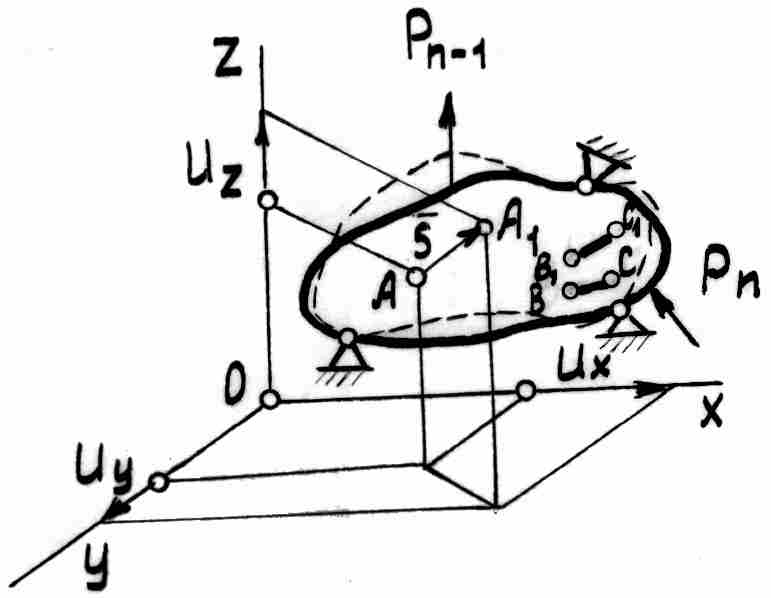Р ис. 1.4

Подобно линейным можно вывести в рассмотрение и угловые перемещения. Рассмотрим достаточно малый линейный элемент тела, занимающий до нагружения положение ВС, а после приложения нагрузок – В₁С₁. При деформировании тела рассматриваемый элемент поворачивается. Угол поворота элемента называется угловым перемещением, он характеризуется вектором, который тоже можно разложить по осям x, y, z . Таким образом, угловое перемещение – это угол между направлениями элемента соответственно до и после деформирования.