
Вищий рівень (15)
Яка повинна бути кінетична енергія протона, налітав на інший, що спочивають протон, щоб їх сумарна кінетична енергія в системі центру інерції була така ж, як у двох протонів, що рухаються назустріч один одному з кінетичними енергіями T = 25,0 ГеВ? . (И. Е. Иродов Задачи по общей физике 1.386)
Нейтрон з кінетичною енергією Т = 2
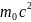 ,
де
- його маса спокою, налітає на інший, що
спочивають нейтрон. визначити: а) сумарну
кінетичну енергію Т обох нейтронів в
системі їх центру інерції і імпульс р
кожного нейтрона в цій системі; б)
швидкість центру інерції цієї системи
частинок. . (И. Е. Иродов
Задачи по общей физике 1.384)
,
де
- його маса спокою, налітає на інший, що
спочивають нейтрон. визначити: а) сумарну
кінетичну енергію Т обох нейтронів в
системі їх центру інерції і імпульс р
кожного нейтрона в цій системі; б)
швидкість центру інерції цієї системи
частинок. . (И. Е. Иродов
Задачи по общей физике 1.384)Знайти залежність імпульсу від кінетичної енергії частинки з масою спокою . Обчислити імпульс протона з кінетичною енергією 500 МеВ. . (И. Е. Иродов Задачи по общей физике 1.375)
Знайти швидкість, при якій кінетична енергія частинки дорівнює її енергії спокою. 1.373
У скільки разів релятивістська маса частинки, швидкість якої відрізняється від швидкості світла на 0,010%, перевищує її масу спокою? . (И. Е. Иродов Задачи по общей физике 1.368)
Використовуючи дані попередньої задачі, визначити час розгону ракети
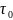 в системі відліку, пов'язаної з самою
ракетою. Мати на увазі, що цей час
визначається формулою
в системі відліку, пов'язаної з самою
ракетою. Мати на увазі, що цей час
визначається формулою
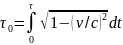 , де
, де
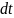 – інтеграл часу в системі Землі. .
(И. Е. Иродов Задачи по
общей физике 1.367)
– інтеграл часу в системі Землі. .
(И. Е. Иродов Задачи по
общей физике 1.367)
«Спочиваючі прямий конус має кут напіврозчину
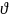 =
=
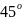 і площа бічної поверхні
і площа бічної поверхні
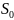 = 4,0
= 4,0
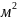 .
Знайти в системі відліку, що рухається
зі швидкістю v = 4 / 5 з
вздовж осі конуса: а) його кут напіврозчину
', б) площа бічної поверхні. .
(И. Е. Иродов Задачи по общей физике
1.343)
.
Знайти в системі відліку, що рухається
зі швидкістю v = 4 / 5 з
вздовж осі конуса: а) його кут напіврозчину
', б) площа бічної поверхні. .
(И. Е. Иродов Задачи по общей физике
1.343)З якою швидкістю рухалися в K -системі відліку годинник, якщо за час t = 5,0 с (в K-системі) вони відстали від годинника цієї системи на
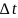 = 0,10 с? . (И. Е. Иродов
Задачи по общей физике 1.344)
= 0,10 с? . (И. Е. Иродов
Задачи по общей физике 1.344)«Стрижень пролітає з постійною швидкістю повз мітки, нерухомою в K -системі відліку. Час прольоту = 20 нc - в K -системі. У системі ж відліку, пов'язаної зі стрижнем, мітка рухається вздовж нього протягом '- 25 нc. Знайти власну довжину стрижня. . (И. Е. Иродов Задачи по общей физике 1.345)
Власний час життя деякою нестабільною частки = 10 нc. Знайти шлях, який пролетить ця частка до розпаду в лабораторній системі відліку, де її час життя = = 20 нc. . (И. Е. Иродов Задачи по общей физике 1.346)
В K -системі відліку мю-мезон, що рухається зі швидкістю V = 0,990 с, пролетів від місця свого народження до точки розпаду відстань I = 3,0 км. Визначити: а) власне час життя цього мезона; б) відстань, яку пролетів мезон в K -системі з «його точки зору». . (И. Е. Иродов Задачи по общей физике 1.347)
Два стрижня однаковою власної довжини
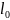 рухаються назустріч один одному
паралельно загальної горизонтальної
осі. В системі відліку, пов'язаної з
одним зі стрижнів, проміжок часу між
моментами збіги лівих і правих кінців
стрижнів виявився рівним
.
Яка швидкість одного стрижня щодо
іншого? . (И. Е. Иродов
Задачи по общей физике 1.350)
рухаються назустріч один одному
паралельно загальної горизонтальної
осі. В системі відліку, пов'язаної з
одним зі стрижнів, проміжок часу між
моментами збіги лівих і правих кінців
стрижнів виявився рівним
.
Яка швидкість одного стрижня щодо
іншого? . (И. Е. Иродов
Задачи по общей физике 1.350)Частинка з масою спокою в момент t = 0 починає рухатися під дією постійної сили F. Знайти залежність від часу t швидкості частинки і пройденого нею шляху. . (И. Е. Иродов Задачи по общей физике 1.378)
Енергія фотона в K -системі дорівнює
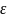 .
Скориставшись формулами перетворення,
наведеними в попередній задачі, знайти
енергію
'
цього фотона в K' -системі,
що переміщається зі швидкістю V щодо K
-системи в напрямку руху фотона. При
якому значенні V енергія фотона
' =
/ 2? . (И. Е. Иродов Задачи
по общей физике 1.382)
.
Скориставшись формулами перетворення,
наведеними в попередній задачі, знайти
енергію
'
цього фотона в K' -системі,
що переміщається зі швидкістю V щодо K
-системи в напрямку руху фотона. При
якому значенні V енергія фотона
' =
/ 2? . (И. Е. Иродов Задачи
по общей физике 1.382)Показати, що для частинки величина
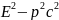 є інваріант, тобто має одне і те ж
значення у всіх інерціальних системах
відліку. Яке значення цього інваріанта?
. (И. Е. Иродов Задачи по
общей физике 1.383)
є інваріант, тобто має одне і те ж
значення у всіх інерціальних системах
відліку. Яке значення цього інваріанта?
. (И. Е. Иродов Задачи по
общей физике 1.383)
Методичні вказівки
Нижчий рівень.
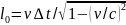
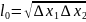 ;
;
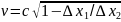
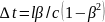
A)
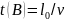 ,
,
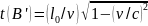 ;
b)
;
b)
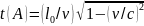 ,
,
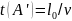 .
.Для цього потрібно впевнитись в тому, що при
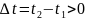 і
і
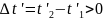
Скористайтесь інваріантністю інтервала.
Оптимальний рівень.
A)
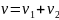 ;
b)
;
b)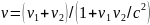 .
.A)
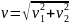 ;
b)
;
b)
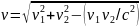
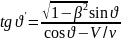 ;
;
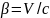 .
.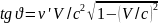 .
.A)
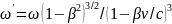 ;
b)
;
b)
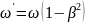 ;
.
;
.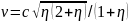 ;
тут с – швидкість світла.
Тут використано визначення густини як
відношення маси спокою тіла до його
об’єму.
;
тут с – швидкість світла.
Тут використано визначення густини як
відношення маси спокою тіла до його
об’єму.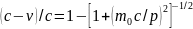 .
.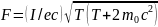 ;
;
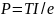 .
.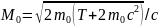 ;
;
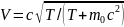 .
.
Вищий рівень
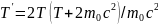 .
.A)
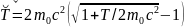 ;
;
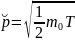 ;
b)
.
;
b)
.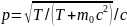
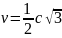 .
.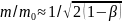 .
.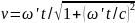 ;
;
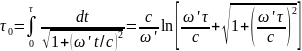 .
.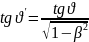 ;
;
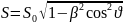 .
.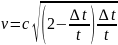 .
.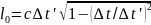 .
.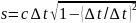 .
.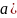
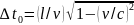 ;
b)
;
b)
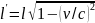
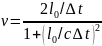 .
.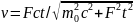 ;
;
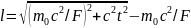 .
.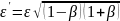 ,
де
,
,
де
,
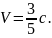
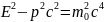 ,
де
- маса спокою частинки.
,
де
- маса спокою частинки.
