4. Плоская волна, для которой и ( и ), остается плоской волной во всех исо.

Из последнего вывода – об инвариантности плоской волны – следует, что если поле в некоторой пространственно-временной точке равно нулю, то это утверждение объективно и не зависит от того, в какой ИСО рассматривается эта точка. Иначе говоря, векторы электромагнитного поля в данной пространственно-временной точке во всех системах отсчета равны нулю, т.е. фаза волны во всех системах отсчета одинакова, что доказывает ее инвариантность.

Фаза плоской электромагнитной волны – релятивистский инвариант.

Инвариантность фазы следует из формул преобразования векторов поля.

Фаза волны может быть представлена в виде .

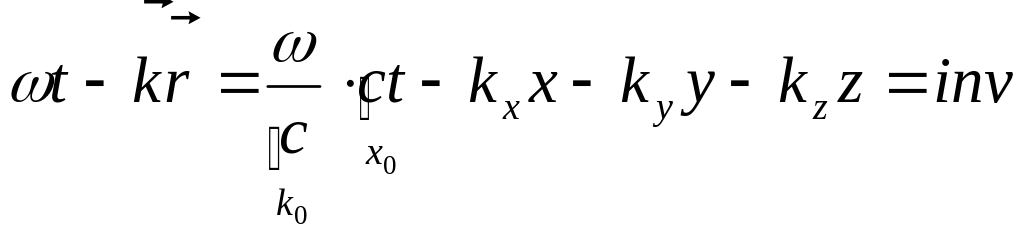Правая часть выражения имеет вид скалярного произведения. Совокупность величин, стоящих в правой части, может быть представлена в виде 4^х-вектора: , или .

Тогда при переходе из одной системы отсчета в другую величины, образующие 4^х-вектор, будут изменяться в соответствии с преобразованиями Лоренца.

Если система отсчета движется со скоростью в направлении оси неподвижной системы, то

.

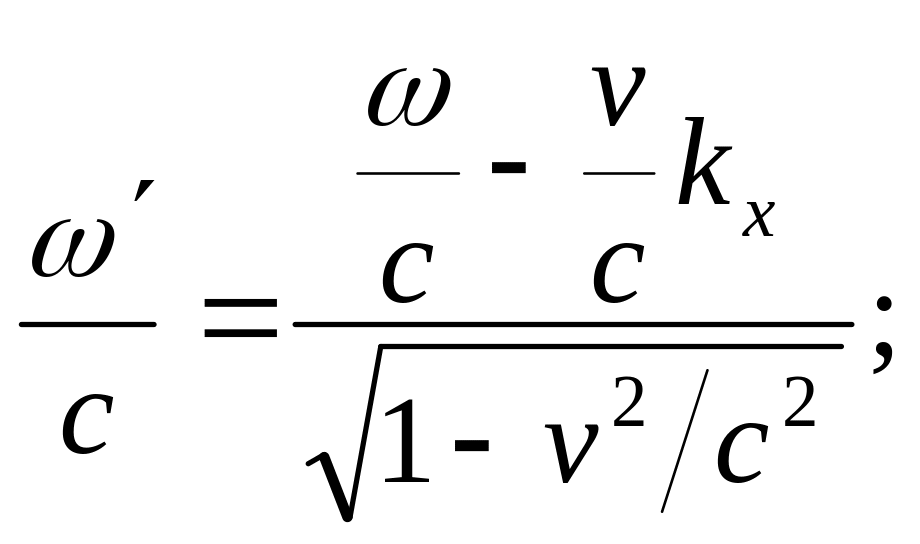
Пусть угол между векторами и (направлением движения и линией наблюдения),

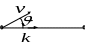тогда , где ,

т.е., если частота электромагнитных колебаний, излучаемых

неподвижным в системе отсчета источником, то частота колебаний, воспринимаемых приемником, движущимся вместе с системой со скоростью .

Излучаемая источником частота может быть найдена по измеренной приемником частоте как

.

Изменение частоты, регистрируемой приемником по отношению к частоте излучателя, обусловленное их относительным движением со скоростью , называется эффектом Доплера.