
- •2. На рис. 1.5 приведена более полная по сравнению с рис. 1.4 типовая функциональная схема сау, на которой показаны основные составные части управляющего устройства: чу, ву, иу.
- •3. Рассмотрим классификацию сау по ряду признаков, существенных с точки зрения теории управления.
- •4. По характеру звеньев, включаемых в сау, системы делятся на линейные и нелинейные.
- •10. Из типовых функций времени наиболее часто используются две: единичная импульсная функция и единичная ступенчатая функция.
- •12. В частном случае при чисто мнимых значениях параметра р формула определяет частотную характеристику линейной системы:
- •13. На основании изложенного выше для линейной стационарной системы (2.5.3) перепишется в следующем виде: .(2.6.1)
12. В частном случае при чисто мнимых значениях параметра р формула определяет частотную характеристику линейной системы:
 . (2.5.1)
. (2.5.1)
Следовательно,
частотная характеристика линейной
системы есть отношение реакции линейной
системы на гармонические колебания
единичной амплитуды и частоты
к этой гармонической функции eit.
На основании (2.5.1) реакция линейной
системы на гармонические колебания
данной частоты
и единичной амплитуды eit
равна произведению значения частотной
характеристики системы при данном
значении частоты на входную функцию
eit:
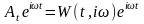 .
.
Найдем реакцию линейной системы на входные гармонические колебания произвольной амплитуды а и фазы :
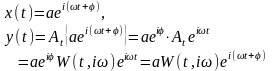 (2.5.2)
(2.5.2)
Частотная
характеристика линейной системы в
общем случае является комплексной
функцией, поэтому ее можно представить
в показательной форме: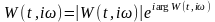 .(2.5.3)
.(2.5.3)
Подставляя (2.5.3) в (2.5.2), получим:
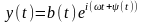 ,
,
где
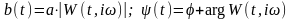
Эта формула показывает, что линейная система реагирует на гармонические колебания входной величины в общем случае колебаниями переменной амплитуды b(t) и переменного сдвига фазы (t).
Пользуясь
частотной характеристикой линейной
системы (2.5.1), можно связь (2.4.3) между
выходом и выходом системы записать в
следующем виде:
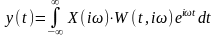 . (2.5.4)
. (2.5.4)
Сравнивая формулу (2.5.4) с формулой (2.3.9) видим, что они имеют много общего: за характеристику системы принимается некоторая функция двух переменных (текущего времени и какого-либо параметра). В (2.3.9) в качестве такого параметра принимается момент действия единичного импульса, а в (2.5.4) – круговая частота гармонического колебания . Однако из (2.5.4) следует, что применение частотных характеристик включает лишнюю операцию перехода к преобразованию Фурье. И это будет общей закономерностью.
Какими бы типовыми элементарными воздействиями мы не пользовались, кроме -функции, нужно находить какое-то преобразование входного воздействия, а потом уже определять выходную переменную системы. И только использование в качестве элементарного воздействия -функции дает существенное упрощение, так как при этом исключается необх-сть дополнительного преобразования входного воздействия.
Следовательно, для произвольных линейных систем применение частотных характеристик нерационально. Только для систем с медленно изменяющимися параметрами (т.е. параметры системы можно считать постоянными на значительных промежутках времени) целесообразно использование частотных характеристик.
Именно поэтому частотные характеристики широко используются для исследования стационарных линейных систем.
13. На основании изложенного выше для линейной стационарной системы (2.5.3) перепишется в следующем виде: .(2.6.1)
Эту
характеристику называют амплитудно-фазовой
частотной характеристикой (АФХ) (в
литературе иногда используются выражение
«частотная передаточная функция»)
стационарной линейной системы. Здесь
A()=|W(i)|
- амплитудная частотная характеристика,
а
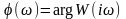 - фазовая частотная характеристика. Из
(2.6.1) следует, что частотные характеристики
линейной стационарной системы являются
функцией одного параметра – частоты
гармонических колебаний. Именно этим
объясняется широкое использование
частотных методов исследования в
классический период развития ТАР и
ТАУ. Графики амплитудной и фазовой
частотных характеристик приведены на
рис. 2.4, причем амплитудная частотная
характеристика (АЧХ) является четной
функцией, т.е. A(-)=A(),
а фазовая частотная характеристика
(ФЧХ) – нечетной функцией, т.е. (-)=-().
- фазовая частотная характеристика. Из
(2.6.1) следует, что частотные характеристики
линейной стационарной системы являются
функцией одного параметра – частоты
гармонических колебаний. Именно этим
объясняется широкое использование
частотных методов исследования в
классический период развития ТАР и
ТАУ. Графики амплитудной и фазовой
частотных характеристик приведены на
рис. 2.4, причем амплитудная частотная
характеристика (АЧХ) является четной
функцией, т.е. A(-)=A(),
а фазовая частотная характеристика
(ФЧХ) – нечетной функцией, т.е. (-)=-().
Графически амплитудно-фазовая частотная характеристика изображается на комплексной плоскости (рис. 2.5) в полярных координатах (А, ) как годограф функции W(i).

Однако
чаще строят амплитудно-фазовую частотную
характеристику в прямоугольных
координатах (U,V)
(рис.2.5), выделив в выражении W(i)
вещественную и мнимую части

При этом U() называют вещественной частотной характеристикой, а V() – мнимой.
Угол показан на рис.2.5 как отрицательный (отложен по часовой стрелке), так как чаще всего реакция на выходе звена имеет отставание по фазе по сравнению с входной величиной. При этом частоту изменяют от 0 до (сплошная кривая на рис.2.5) или от - до + , тогда добавляется еще симметричная к ней пунктирная кривая.
15. На практике чаще всего амплитудную и фазовую частотные характеристики изображают в логарифмическом масштабе.
Построенные таким образом частотные характеристики называются логарифмическими частотными характеристиками.
Логарифмическая амплитудная частотная характеристика (ЛАХ) строится в виде зависимости
L()=20 lg A()=20 lg|W(i)|,
а логарифмическая фазовая частотная характеристика (ЛФХ) строится в виде зависимости () от lg().
В
качестве единицы измерения величины
L()
используют
децибел:![]()
1 Б соответствует усилению мощности сигнала в 10 раз, 2 Б – в 100 раз и т.д.
Мощность
сигнала пропорциональна квадрату
амплитуды:
![]() ,
поэтому усиление в белах, выраженное
через отношение
амплитуд А, равно
,
поэтому усиление в белах, выраженное
через отношение
амплитуд А, равно![]() .
Следовательно, в децибелах
оно равно 20lgA.
.
Следовательно, в децибелах
оно равно 20lgA.
На
оси абсцисс указываются значения [c-1]
Единицей приращения
lg
является декада, соответствующая
изменению
частоты в 10 раз (иногда используется
октава,
соответствующая изменению частоты
в 2 раза (1 октава равна 0,303 декады, так
как![]() )).
Начало координат обычно помещают
в точке
)).
Начало координат обычно помещают
в точке
![]() ,
так как
,
так как![]() .
Точка пересечения ЛАХ с осью абсцисс
определяет частоту среза ср.
.
Точка пересечения ЛАХ с осью абсцисс
определяет частоту среза ср.
Главное достоинство ЛАХ состоит в возможности их построения практически без вычислительных работ, например, суммированием или в виде асимптотических ЛАХ (совокупности отрезков прямых линий с наклоном, кратным 20 дБ/дек). Кроме того, в логарифмических координатах уменьшается кривизна характеристик.
16. Передаточная функция линейной САУ в общем случае определяется формулой W(t,p)=Atept/ept. (2.8.1)
Реакция стационарной линейной системы на показательное возмущение не зависит от текущего времени, поэтому из формулы (2.8.1) следует, что для стационарного случая Atept=W(p)ept.
Отсюда
получим следующее определение:
передаточной функцией
стационарной линейной системы называется
множитель,
на который умножается показательная
функция
ept,
проходя
через эту систему. Непосредственно из
формулы частотной характеристики для
стационарной линейной системы
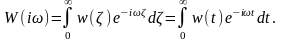 следует,
что
следует,
что
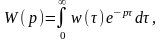 (2.8.2)
т.е.
передаточная функция стационарной
линейной системы является
преобразованием Лапласа от весовой
(импульсной переходной) функции. Для
физически возможной стационарной
линейной
САУ имеем
(2.8.2)
т.е.
передаточная функция стационарной
линейной системы является
преобразованием Лапласа от весовой
(импульсной переходной) функции. Для
физически возможной стационарной
линейной
САУ имеем
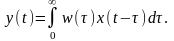 (2.8.3)
(2.8.3)
Из операционного исчисления известно, что интеграл (2.8.3) является интегралом свертки. Обозначая преобразования Лапласа от входной x(t) и выходной y(t) переменных системы соответственно через X(p) и Y(p), учитывая (2.8.2), предполагая равенство нулю всех внешних возмущений и нулевые начальные условия, получим из (2.8.3) следующее выражение для передаточной функции стационарной линейной системы:
![]()
Данное описание является наиболее распространенной детерминированной математической моделью стационарной линейной системы.
19.
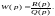 (2.11.1)
(2.11.1)
Выражение
(2.11.1) формально определяет передаточную
функцию стационарной линейной системы,
поведение которой описывается
дифференциальными уравнениями (2.9.8),
при всех значениях р, кроме совпадающих
с корнями характеристического
уравнения системы
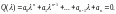 (2.11.2)
(2.11.2)
Однако физически эта передаточная функция существует не при всех значениях р. В общем случае реакция системы на показательное возмущение представляет собой полное решение уравнения (2.9.8), а не частное. Для получения полного решения уравнения (2.9.8) следует к найденному частному решению добавить общее решение соответствующего однородного дифференциального уравнения
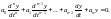 (2.11.3)
(2.11.3)
Из
теории дифференциальных уравнений
известно, что если корни
характеристического уравнения (2.11.2)
v,...,vn все различны, то общее решение
уравнения (2.11.3) представляет собой
линейную комбинацию показательных
функций
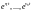 с произвольными коэффициентами. Если
некоторые корни характеристического
уравнения совпадают, например
с произвольными коэффициентами. Если
некоторые корни характеристического
уравнения совпадают, например
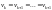 ,
то функции
,
то функции
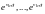 заменяются функциями
заменяются функциями
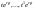 .
Таким образом, в случае, когда
характеристическое уравнение не
имеет кратных корней, общее решение
уравнения (2.9.8) определяется формулой
.
Таким образом, в случае, когда
характеристическое уравнение не
имеет кратных корней, общее решение
уравнения (2.9.8) определяется формулой
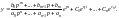 (2.11.4)
(2.11.4)
Для
определения передаточной функции
системы разделим (2.11.4) на ept :
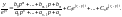 (2.11.5)
(2.11.5)
Если
действительные части всех
разностей
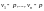 отрицательны, то все показательные
функции в (2.11.5) стремятся к 0 при
отрицательны, то все показательные
функции в (2.11.5) стремятся к 0 при
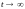 .
В этом случае передаточная функция
системы, представляющая собой отношение
реакции этой системы на бесконечно
долго действующее на нее возмущение
ерt к самому возмущению ерt, определяется
формулой (2.11.1). Если хотя бы одно из
чисел
.
В этом случае передаточная функция
системы, представляющая собой отношение
реакции этой системы на бесконечно
долго действующее на нее возмущение
ерt к самому возмущению ерt, определяется
формулой (2.11.1). Если хотя бы одно из
чисел
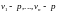 имеет положительную действительную
часть, то соответствующая показательная
функция в (2.11.4) неограниченно возрастает
при
,
и, следовательно, передаточная функция
системы не существует.
имеет положительную действительную
часть, то соответствующая показательная
функция в (2.11.4) неограниченно возрастает
при
,
и, следовательно, передаточная функция
системы не существует.
Таким
образом, передаточная функция стационарной
линейной системы, описываемой
дифференциальным уравнением (2.9.8)
существует только в области значений
р, действительные части которых
больше действительных частей всех
корней
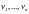 характеристического уравнения (рис.2.5).
характеристического уравнения (рис.2.5).
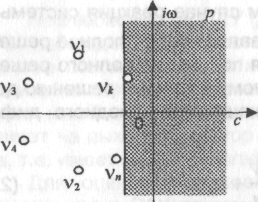
Рис.2.5 - Область существования передаточной функции
Очевидно,
что частотная характеристика,
представляющая собой значение
передаточной функции на мнимой оси
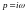 ,
существует для рассматриваемой системы
только в том случае, когда действительные
части всех корней характеристической:
уравнения отрицательны. В дальнейшем
мы увидим, что эт условие необходимо и
достаточно для устойчивости стационар
ной линейной системы.
,
существует для рассматриваемой системы
только в том случае, когда действительные
части всех корней характеристической:
уравнения отрицательны. В дальнейшем
мы увидим, что эт условие необходимо и
достаточно для устойчивости стационар
ной линейной системы.
Все виды динамических характеристик линейных систем (дифференциальное уравнение, передаточная функция, частотные характеристики, весовая (импульсная переходная) функция, переходная функция) связаны между собой определенными зависимостями и эквивалентны друг другу в определении динамических свойств системы, поэтому изложенного выше вполне достаточно для изучения динамических свойств звеньев линейных САУ, описываемых дифференциальными уравнениями.
18. Переменные состояния – это промежуточные переменные системы (рис.2.4), число которых равно ее порядку n. В общем случае u и выходные у переменные могут быть векторными величинами размерности m и l соответственно.

Рис.2.4 – Состояние системы
Переменные
состояния называют также координатами
состояния, так как их совокупность
задает вектор состояния
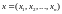 .
.
Множество возможных положений этого вектора образует векторное пространство Х, называемое пространством состояний системы. В переменных состояния САУ описывается векторно-матричным уравнением
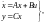 (2.9.9)
(2.9.9)
где
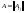 - квадратная матрица коэффициентов (ее
называют также собственной параметрической
матрицей системы);
- квадратная матрица коэффициентов (ее
называют также собственной параметрической
матрицей системы);
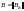 – входная матрица (матрица управления)
системы;
– входная матрица (матрица управления)
системы;
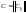 – выходная матрица системы;
– выходная матрица системы;
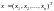 – вектор переменных состояния внутренних
координат системы;
– вектор переменных состояния внутренних
координат системы;
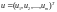 –
вектор входных переменных (управляющих
и возмущающих);
–
вектор входных переменных (управляющих
и возмущающих);
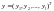 – вектор наблюдаемых или выходных
переменных; размерности матриц А,
В,
С
соответственно
– вектор наблюдаемых или выходных
переменных; размерности матриц А,
В,
С
соответственно
 .
.
Процессы
в САУ в свободном движении (без внешних
воздействий)
согласно уравнению (2.9.9) описываются
векторно-матричным
уравнением
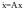 с
характеристическим
уравнением
с
характеристическим
уравнением
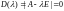 ,
где Е
- единичная
матрица, или в развернутом
виде системой дифференциальных уравнений
,
где Е
- единичная
матрица, или в развернутом
виде системой дифференциальных уравнений

с характеристическим уравнением
 (2.9.10)
(2.9.10)
Эти уравнения при определенных начальных условиях дают возможность изучить процессы в системе путем их решения численными методами с использованием ЭВМ.
Разработаны
различные способы перехода от уравнений
типа
«вход-выход» к уравнениям состояния
вида (2.9.9) и наоборот.
Один из наиболее распространенных
способов состоит в следующем.
Пусть САУ описывается уравнением
(2.9.1). Введем обозначения
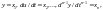
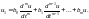
С помощью этих обозначений преобразуем уравнение (2.9.1) к следующему виду:
 (2.9.11)
где
(2.9.11)
где
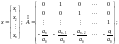
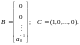
В нашем примере у и и1 являются скалярными величинами. В общем случае (2.9.9) - это, соответственно, вектор наблюдаемых или выходных переменных и вектор входных переменных (управляющих и возмущающих), поэтому в (2.9.11) матрицы В и С выродились в вектор-столбец и вектор-строку соответственно.
Система
уравнений (2.9.11) представляет собой
описание линейной
непрерывной системы в пространстве
состояний
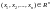 .
Уравнения (2.9.11) с матрицей
.
Уравнения (2.9.11) с матрицей
 называют
уравнениями
в форме Фробениуса. Если
называют
уравнениями
в форме Фробениуса. Если
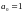 ,
то
,
то
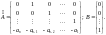
Форма
уравнений (2.9.11) с подобными матрицами
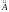 и
В
называется
в ТАУ канонической формой фазовой
переменной.
и
В
называется
в ТАУ канонической формой фазовой
переменной.
Для современной ТАУ как математической теории характерно то, что в ней важное место занимает исследование принципиальной возможности синтеза алгоритмов оценивания, идентификации, управления и адаптации. Эта возможность в значительной степени выявляется при изучении свойств системы, которые принято называть наблюдаемостью, идентифицируемостью, управляемостью и адаптируемостью. Заметим, что часто между наблюдаемостью и идентифицируемостью не делают различий, а адаптируемость рассматривают как частный случай управляемости. Разъясним суть понятий управляемости и наблюдаемости в САУ.
Управляемость
САУ - САУ управляема (полностью
управляема),
если она может быть переведена в
произвольный момент
времени
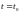 из любого начального состояния x(t0)
в
любое
другое
из любого начального состояния x(t0)
в
любое
другое
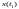 путем приложения кусочно-непрерывного
воздействия
путем приложения кусочно-непрерывного
воздействия
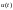 ,
,
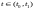 за конечный интервал времени
за конечный интервал времени
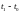 .
.
Наблюдаемость САУ (дуальное понятие управляемости) – САУ наблюдаема (полностью наблюдаема), если все ее переменные состояния можно непосредственно или косвенно определить по выходному (измеряемому) вектору системы. При наличии какой-либо переменной состояния, изменение которой не влияет на выходной вектор САУ, система не вполне наблюдаема, т.е. имеет место неполная наблюдаемость.
Для
оценки управляемости и наблюдаемости
линейных стационарных
САУ применяют критерии Гильберта и
Калмана. Первый
из них основан на использовании
канонического уравнения состояния.
Второй использует матрицы управляемости
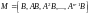 размерности
п
размерности
п (п
(п т)
или
матрицы
наблюдаемости
т)
или
матрицы
наблюдаемости
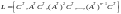 размерности
размерности
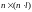 .
Например,
если матрицы М
и L
имеют
ранг
п,
то
САУ полностью управляема и наблюдаема.
.
Например,
если матрицы М
и L
имеют
ранг
п,
то
САУ полностью управляема и наблюдаема.
Принцип дуальности (двойственности) дает возможность оценивать по условиям наблюдаемости одной САУ управляемость другой (сопряженной) или по условиям управляемости – наблюдаемость другой сопряженной системы.
17.
20.
Передаточные
функции стационарных линейных систем,
описываемых обыкновенными дифференциальными
уравнениями, являются отношениями
полиномов с действительными коэффициентами.
Такие полиномы имеют только действительные
и комплексные попарно сопряженные
корни. При разложении этих полиномов
на множители каждый действительный
корень даст линейный относительно
р двучлен,
а каждая пара комплексно сопряженных
корней – квадратный трехчлен относительно
р с
действительными коэффициентами. Каждый
нулевой корень даст дополнительный
множитель р.
Поэтому
отношение полиномов (2.11.1) можно
переписать в следующем виде:
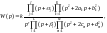 (2.12.1)
где
(2.12.1)
где
 – любое целое число.
– любое целое число.
Для исследования стационарных линейных систем удобно ввести элементарные типовые стационарные линейные звенья, передаточными функциями которых являются отдельные простейшие множители в формуле (2.12.1):
идеальный
дифференциатор
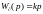 ;
;
форсирующее
звено 1-го порядка
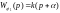 ;
;
форсирующее
звено 2-го порядка
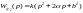 ;
;
идеальный интегратор Wu(p) = k/p;
статическое
звено 1-го порядка
 ;
;
-
статическое
звено 2-го порядка
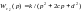 .
.
Перечисленных
шести элементарных типовых звеньев
вполне достаточно для исследования
систем, описываемых уравнениями вида
(2.9.1), (2.9.8). Иногда целесообразно
рассматривать как отдельное
элементарное звено идеальный
безынерционный усилитель –
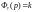 .
.
21.
