Содержание задания:
Предварительная подготовка к рассмотрению темы, заключающая в составление и записи студентами под руководством преподавателя краткого конспекта формул, необходимых для решения задач, которые известны из ранее прошедшего лекционного занятия;
рассмотрение примеров физических явлений, изучаемых в данной теме, приводимых студентами, которые известны из повседневного была, личного опыта, промышленного использования или лабораторных работ.
Решение и обсуждение студентами (индивидуально или триадами) под руководством преподавателя следующих задач:
Вычислить момент инерции:
Медного однородного диска относительно оси симметрии, перпендикулярной к плоскости диска, если его толщина
и
радиус
.Однородного сплошного конуса относительно его оси симметрии, если масса конуса и радиус его основания
.
Р
ешение:
Момент инерции характеризует распределение массы в теле и вычисляется как
(1).
Масса
тела равна
,
объем диска (или цилиндра)
.
Переменной
величиной в данном случае будет радиус
(
),
т.к. вращение рассматривается относительно
оси симметрии перпендикулярной к
плоскости диска.
Вычислим
элемент массы
.
Т
огда
момент инерции
,
подставим значения для радиуса, толщины
и плотности
Масса тела равна , элемент массы
.
Объем конуса
.
Выделим из конуса дисковый элемент
радиуса
и бесконечно малой высотой
,
объем такого элемента
,
а
.
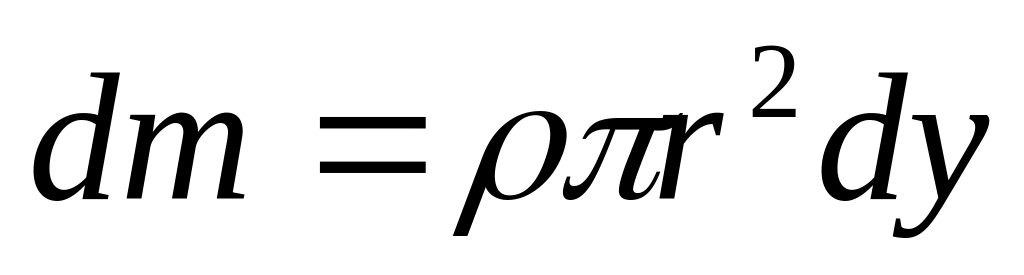Момент инерции этого дискового элемента
Определим
из
треугольника (рис. 1.257.(б, 2)):
,
а также
,
- угол полураствора конуса. Тогда
.
Элемент массы
.
Тогда момент инерции конуса
,
т.к.
,
то
.
Момент
инерции конуса равен
.
Ответ:
.
Однородный цилиндр радиуса R раскрутили вокруг его оси до угловой скорости ω и поместили в угол. Коэффициент трения между стенками угла и поверхностью цилиндра равен μ. Сколько оборотов сделает цилиндр до остановки?
Р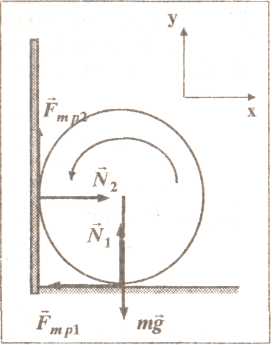
ешение:
На
вращающийся в углу цилиндр действуют:
Земля с силой тяжести
,
горизонтальная поверхность с силами
и
,
а также вертикальная поверхность с
силами
и
,
причем, силы трения являются силами
трения скольжения, поэтому справедливы
соотношения:
и
Применим основное уравнение динамики вращательного движения, согласно которому
Учитывая,
что момент инерции сплошного цилиндра
относительно оси, проходящей через
центр масс, равен
и вычисляя моменты указанных сил
,
и
получаем:
(1)
Поскольку
центр масс цилиндра неподвижен (
),
векторная сумма действующих на него
сил равна нулю:
Спроектируем это выражение на оси координат:
Ох:
и
(2)
Oy:
и
(3)
Из
уравнений (2) и (3) найдем
и
:
и
Подставим
их в (1):
Отсюда получаем выражение для углового ускорения:
(4)
Решение "динамической" части задачи приводит к заключению, что вращение происходит с постоянным угловым ускорением. Следовательно, при решении кинематической части задачи можно воспользоваться законами движения в виде:
К
моменту остановки
,
где N - число оборотов,
поэтому
Выразив
из последнего уравнения
и подставив это значение в первое
кинематическое уравнение, получим:
Подставляя выражение для углового ускорения (4), находим:
.
Ответ:
.
Однородный диск радиуса R имеет круглый вырез. Масса оставшейся (заштрихованной) части диска равна m. Найти момент инерции такого диска относительно оси, перпендикулярной плоскости диска и проходящей:
а) через точку О;
б) через его центр масс.
Домашняя работа: №№ 1.306, 1.279, 1.295. Иродов И.Е. Задачи по общей физики. М.: Бином. Лаб. знаний, 2007
Практическое занятие № 15 «Кинетическая энергия движения твердого тела, кинетическая энергия вращения»
Закрепление теоретических сведений, результатов лабораторных практикумов и навыков расчета величин в рамках темы «Динамика твердого тела»