
Министерство образования и науки Российской Федерации
Иркутский государственный технический университет
Факультет Физико-технический институт
Кафедра квантовой физики и нанотехнологий
ОБЩАЯ ФИЗИКА. МЕХАНИКА
Методические указания по практическим занятиям
для студентов, 210000 «Электронная техника, радиотехника, связь»
«Наименование укрупненной группы направлений и специальности»
специальности: 210600 «Нанотехнология»,
специализации 210602 «Наноматериалы»
Иркутск
2006 г.
ВВЕДЕНИЕ
Аудиторные занятия включают следующий перечень занятий:
лекции, на которых сообщается теоретический материал;
семинарские занятия, на которых прививается навык решения задач и числовых расчетов величин;
лабораторный практикум, на котором прививается навык моделирования явлений и измерения физических величин.
Лекционные занятия не предусматривают заданий для аудиторной работы.
Представленный список тем является основой для проведения семинарских занятий и может быть дополнен с изменением лекционного материала.
Список тем для семинарских занятий:
Способы описания движения материальной точки. Перемещение, скорость, ускорение в векторной и координатной формах – 4 часа
Произвольное криволинейное движение, кривизна траектории, радиус, центр кривизны – 2 часа
Разложение вектора полного ускорения на нормальную и тангенциальную составляющие. Движение точки по окружности, векторы угловой скорости и углового ускорения– 4 часа
Релятивистская механика. Инвариантность длины, интервала времени, ускорения– 2 часа
Сокращение длины и изменение формы движущихся тел – 2 часа
Силы и взаимодействия. Первый, второй законы Ньютона. Третий закон Ньютона. – 4 часа
Понятие импульса тела, импульса силы; момента импульса, момента силы. Уравнение моментов– 4 часа
Система материальных точек, ее импульс, уравнение моментов для системы материальных точек. Центр масс - 2 часа
Работа силы. Кинетическая энергия. -2 часа
Силовое поле. Связь силы с потенциальной энергией-2 часа
Законы сохранения импульса, момента импульса и энергии. Упругие и неупругие столкновения. Законы сохранения при столкновениях-2 часа
Поступательное, вращательное движение твердого тела, мгновенные оси вращения. Понятие момента инерции относительно оси вращения. Уравнение движения твердого тела. -2 часа
Теорема Гюйгенса-Штейнера. Расчеты моментов инерции полого, сплошного цилиндра, шара, стержня, диска. -2 часа
Кинетическая энергия движения твердого тела, кинетическая энергия вращения. -2 часа
Закон всемирного тяготения Ньютона. Законы Кеплера. Движение искусственных спутников Земли -2 часа
Общие требования к форме отчетности по работам и заданиям состоят в следующем:
аккуратность и соответствие содержания стандартам (отчеты по лабораторным работам, стандарт ИрГТУ.027-2009);
выполнение работ и заданий в указанных временных рамках;
Общие рекомендации по выполнению лабораторных и практических работ включают:
работу с лабораторным оборудованием и методическими указаниями к нему;
работу с дополнительной современной литературой более узкой специализации, особенно в рамках специальности;
знакомство с научными статьями.
СПЕЦИАЛЬНЫЕ УКАЗАНИЯ ПО КАЖДОМУ ЗАНЯТИЮ
Практическое занятие № 1 «Способы описания движения материальной точки. Перемещение, скорость, ускорение в векторной и координатной формах» - 4 часа
Закрепление теоретических сведений, результатов лабораторных практикумов и навыков расчета величин в рамках темы «Механика. Кинематика»
Содержание задания:
Предварительная подготовка к рассмотрению темы, заключающая в составление и записи студентами под руководством преподавателя краткого конспекта формул, необходимых для решения задач, которые известны из ранее прошедшего лекционного занятия;
рассмотрение примеров физических явлений, изучаемых в теме «Механика. Кинематика», приводимых студентами, которые известны из повседневного быта, личного опыта, промышленного использования или лабораторных работ.
Решение и обсуждение студентами (индивидуально или триадами) под руководством преподавателя следующих задач:
Два тела бросили одновременно из одной точки: одно – вертикально вверх другое – под углом
 к горизонту. Начальная скорость каждого
тела v0
.Найти
расстояние между телами через t
c.
к горизонту. Начальная скорость каждого
тела v0
.Найти
расстояние между телами через t
c.
Решение:
![]()
![]()
![]()
![]()
Ответ:
![]()
Радиус-вектор частицы меняется со временем t по закону r = bt(1-
 t),
где b – постоянный вектор,
-
положительная постоянная. Найти:
t),
где b – постоянный вектор,
-
положительная постоянная. Найти:
а) скорость и ускорение частицы как функции t;
б) время, через которое частица вернется в исходную точку, и пройденный при этом путь.
Решение:
а)
v=![]() =b(1-
t)-
bt=
b(1-2
t), a=
=b(1-
t)-
bt=
b(1-2
t), a=![]() =
-2
b
=
-2
b
б)
r(![]() =0
=0 ![]() =0;1/
=0;1/
s=![]()
Ответ:
а) v=b(1-2
t),
a=-2
b;
б)
=1/
,
![]()
Частица движется в положительном направлении оси x так, что ее скорость меняется по закону v =
 ,
где
-
положительная постоянная. В момент t =
0 частица находилась в точке х = 0. Найти:
,
где
-
положительная постоянная. В момент t =
0 частица находилась в точке х = 0. Найти:
а) скорость и ускорение частицы как функции t;
б) среднюю скорость за время, в течение которого она пройдет первые s метров пути.
Решение:
а)
v=![]() =
=
![]()
2 = t , x(t)= ( t)2/4 v=x’(t)= 2t/2, a= x’’(t)= 2/2
б)
<v>=![]() =
2t
/4 ,s= x(t) = (
t)2/4
=
2t
/4 ,s= x(t) = (
t)2/4![]() <v>(s)=
<v>(s)=
![]() /2
/2
Ответ: а) v= 2t/2, a= 2/2; б) <v>(s)= /2
Точка движется, замедляясь, по прямой с ускорением, модуль которого зависит от ее скорости v как а =-
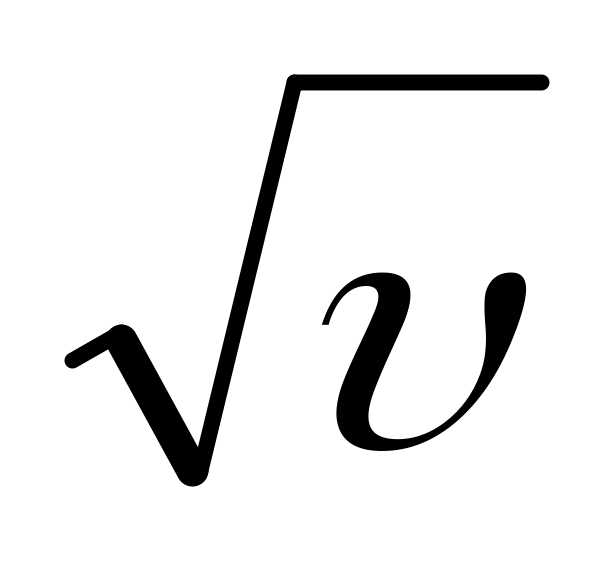 ,
где
- постоянная. В начальный момент скорость
точки равна v0.
Какой путь она пройдет до остановки и
за какое время?
,
где
- постоянная. В начальный момент скорость
точки равна v0.
Какой путь она пройдет до остановки и
за какое время?
Решение:
a=
=-
![]()
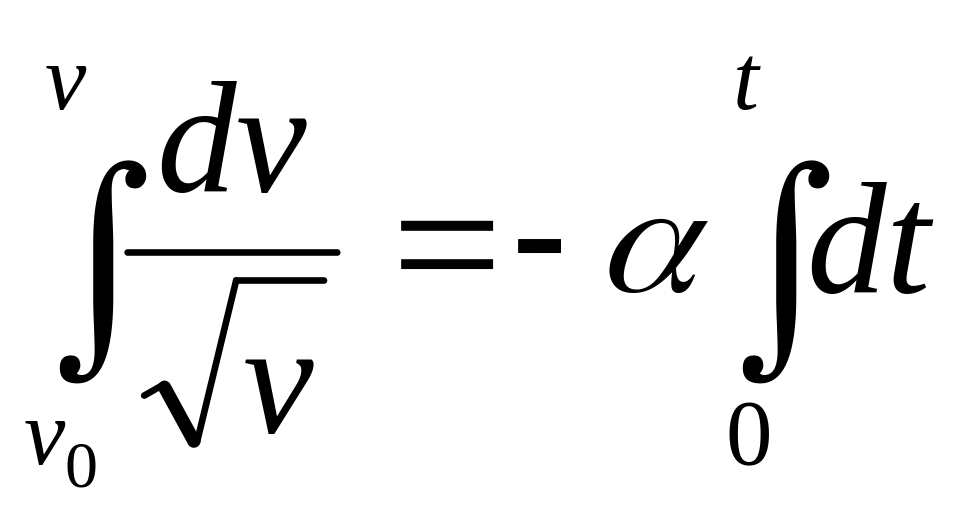
2![]() =
t
v(t)=(
=
t
v(t)=(![]() -
t/2)2
-
t/2)2
v(t)=0
v0=(
t)2/4
t=![]() /
/
s=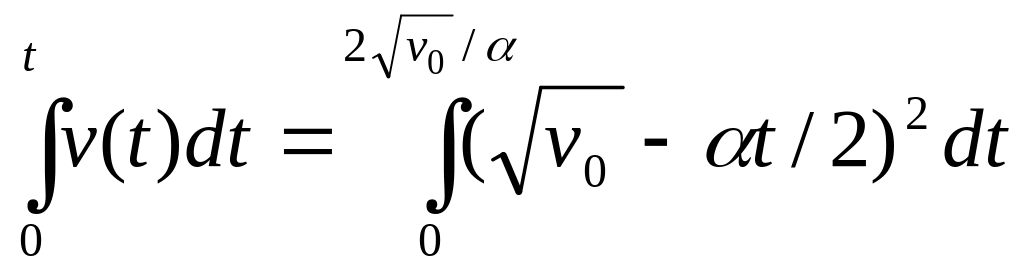 =
=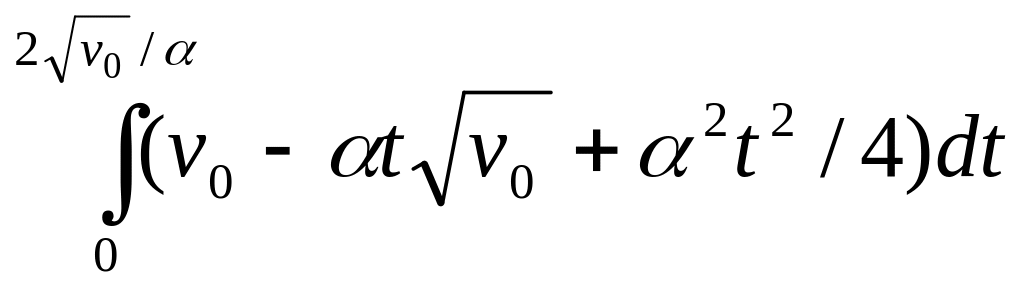 =
=
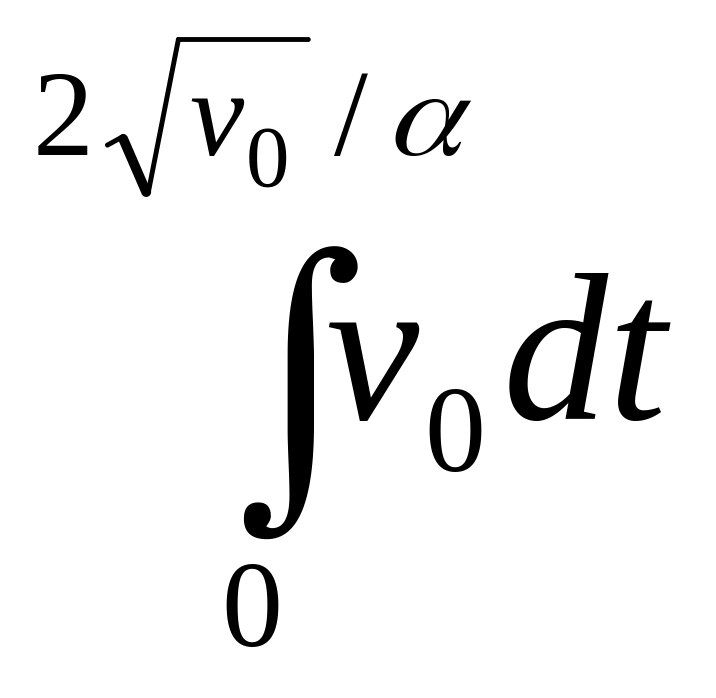 -
-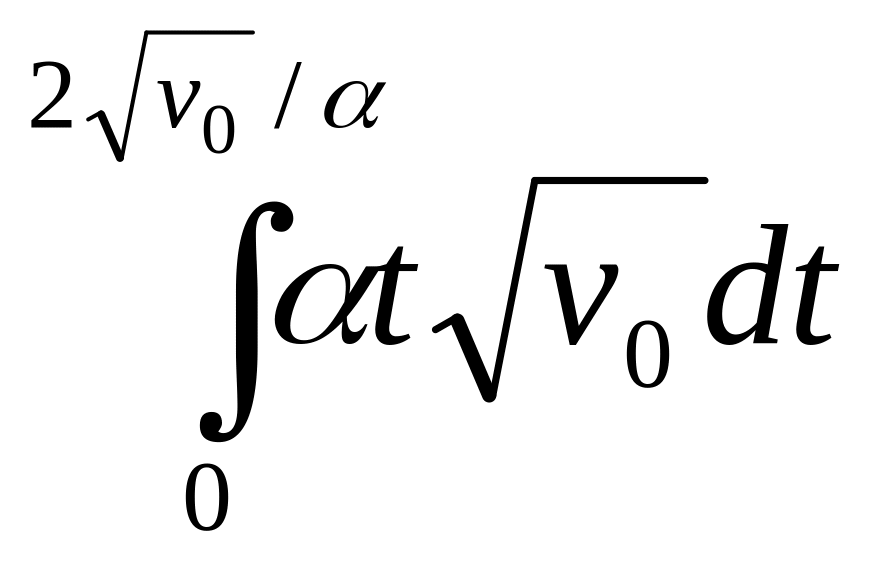 +
+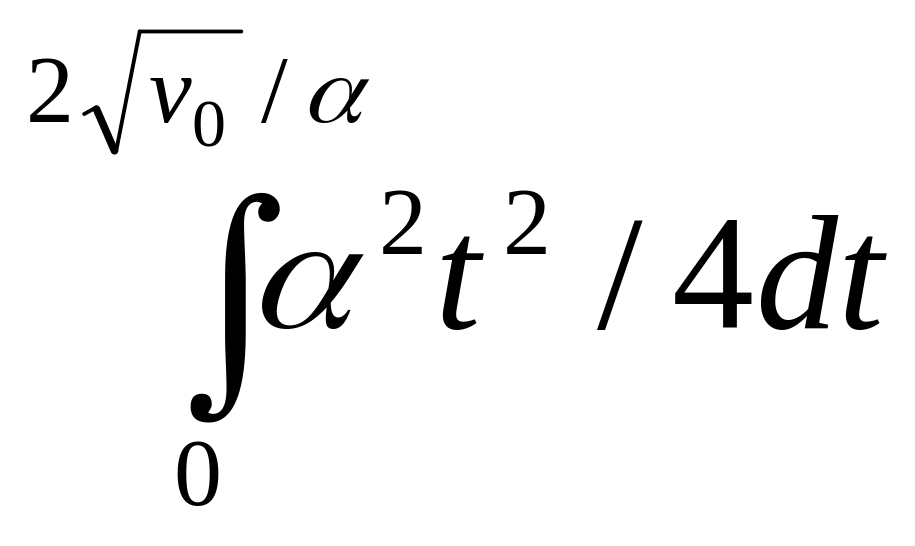 =
=![]()
-![]() +
+![]() =
=
Ответ: s= , t= / .
Точка движется в плоскости xy по закону x=αt, у=βt2, где α и β - положительные постоянные. Найти:
а) уравнение траектории точки у(х) и ее график;
б) модули скорости и ускорения точки как функции t;
в) угол φ между векторами а и v как функцию t.
Решение:
а) ![]() ,
тогда
,
тогда
![]()
б) ![]() ,
,
![]()
![]() ,
получаем
,
получаем
![]() ,
,
![]() ,
,
![]()
![]() ,
получаем
,
получаем
![]()
в) из
скалярного произведения двух векторов
![]() или
или
![]() и
и
![]()
Ответ:
а) ![]() , б)
,
, б)
,
![]() ,
в)
,
в) ![]() .
.
Тело бросили с поверхности земли под углом к горизонту с начальной скоростью v0. Найти:
а) время движения;
б) максимальную высоту подъема и горизонтальную дальность полета; при каком они равны друг другу;
в) уравнение траектории y(x), где у и х – перемещения тела по вертикали и горизонтали соответственно.
Решение:
![]()
![]()
а) y=0 v0t sin - gt2пол/2 = 0 tпол=2 v0 sin /g
б) vy=0 tпод = v0sin /g H = x(tпод )=v02sin2 /2g
L = y(tпол ) = v02sin2 /g Н = L v02sin2 /2g = v02sin2 /g
sin = 4cos =arctg4
в) t=x/ v0cos
y(x) = v0 (x/ v0cos )sin - g( x/ v0cos )2/2 =x tg - gx2 / 2v02cos2
Ответ: а) tпол = 2 v0 sin /g , б) H = x (tпод )=v02sin2 /2g, L = y(tпол ) = v02sin2 /g Н = L при = arctg4, в)y (x) = x tg - gx2 / 2v02cos2 .
Шарик начал падать с нулевой точки, с нулевой начальной скоростью
 на гладкую наклонную плоскость,
составляющую угол
на гладкую наклонную плоскость,
составляющую угол
 с горизонтом. Пролетев расстояние h, он
упруго отразился от плоскости. На каком
расстоянии от места падения шарик
отразился второй раз?
с горизонтом. Пролетев расстояние h, он
упруго отразился от плоскости. На каком
расстоянии от места падения шарик
отразился второй раз?
Решение:
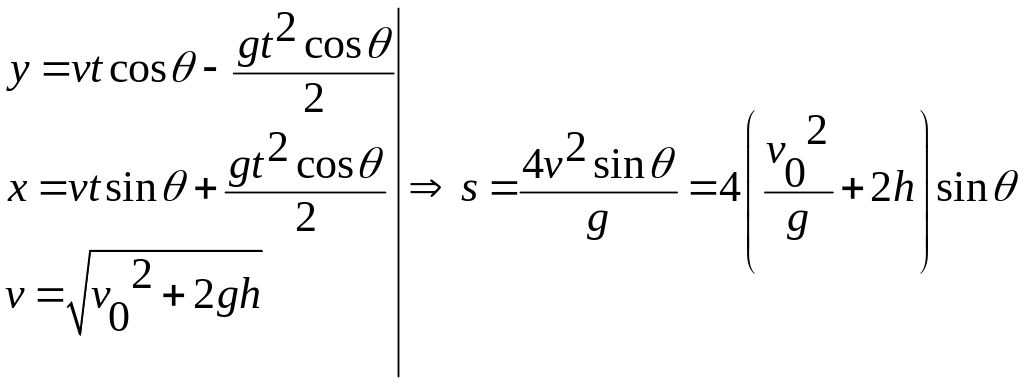
Ответ:
![]()
Воздушный шар начинает подниматься с поверхности земли. Скорость его подъема постоянна и равна v0 . Благодаря ветру шар приобретает горизонтальную компоненту скорости vх = y, где - постоянная, у – высота подъема. Найти зависимость от высоты подъема:
а) сноса шара х(у);
б) полного, тангенциального и нормального ускорений шара.
Решение:
а) v= = y *dy
ydy=![]() dx
dx ![]()
y2/2= v0x x= y2/2v0
б)
![]()
![]() a=
a=![]() ,
,
![]()
![]()
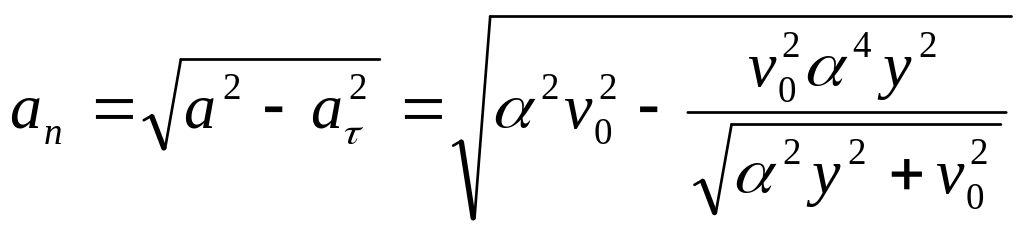 =
=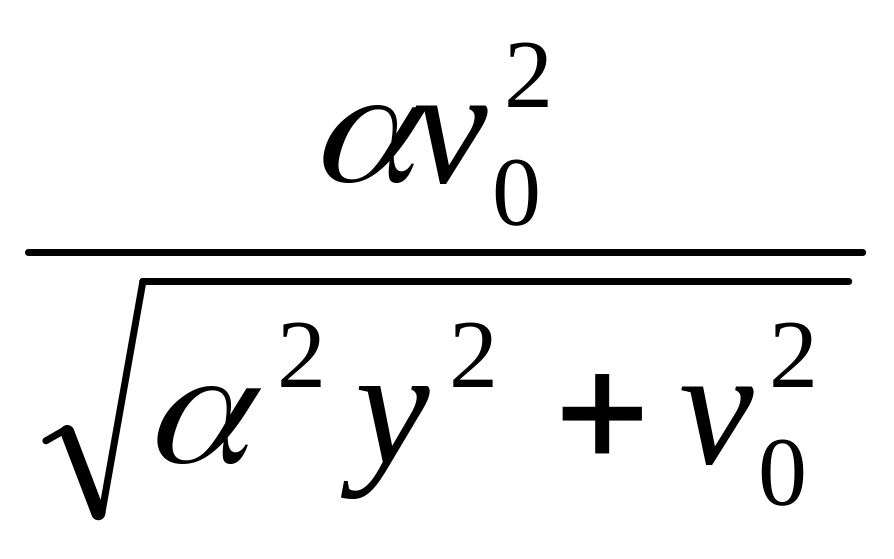
Ответ:
а) x=
y2/2v0,
б)
![]()
![]() =
=
Домашняя работа: №№ 1.16, 1.11, 1.7, 1.3, 1.21, 1.31, 1.32, 1.29, 1.28, 1.25 Иродов И.Е. Задачи по общей физики. М.: Бином. Лаб. знаний, 2007
Практическое занятие № 2 «Произвольное криволинейное движение, кривизна траектории, радиус, центр кривизны»
Закрепление теоретических сведений, результатов лабораторных практикумов и навыков расчета величин в рамках темы «Кинематика механического движения»
Содержание задания:
Предварительная подготовка к рассмотрению темы, заключающая в составление и записи студентами под руководством преподавателя краткого конспекта формул, необходимых для решения задач, которые известны из ранее прошедшего лекционного занятия;
рассмотрение примеров физических явлений, изучаемых в данной теме, приводимых студентами, которые известны из повседневного была, личного опыта, промышленного использования или лабораторных работ.
Решение и обсуждение студентами (индивидуально или триадами) под руководством преподавателя следующих задач:
Частица движется в плоскости ху со скоростью
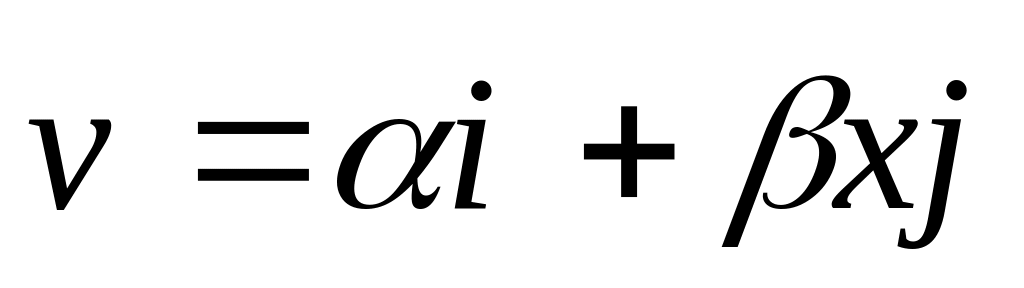 ,
где
,
где
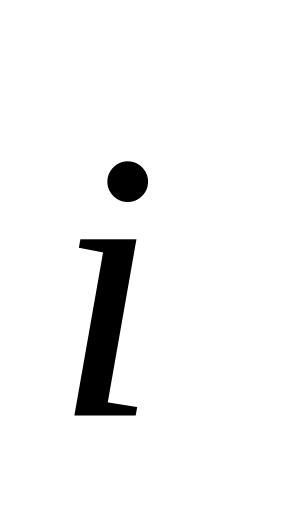 и
и
 — орты осей х и у,
и
— орты осей х и у,
и
 — положительные постоянные. В начальный
момент частица находилась в начале
координат. Найти:
— положительные постоянные. В начальный
момент частица находилась в начале
координат. Найти:
а) уравнение траектории частицы у(х);
б) радиус кривизны траектории как функцию х.
Решение:
а)
![]() ,
,
![]() ,
тогда
,
тогда
![]() и
и
![]() ,
,
![]() .
.
б)
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
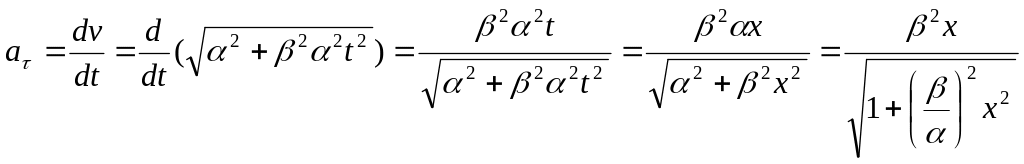
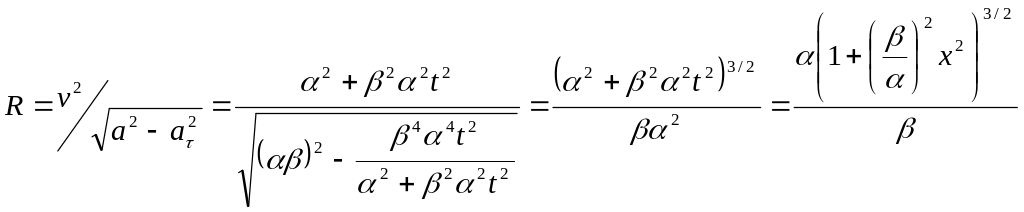
Ответ:
а)
![]() ,
б)
,
б)
![]() .
.
Частица движется равномерно со скоростью v по плоской траектории у(х). Найти ускорение частицы в точке х =0 и радиус кривизны траектории в этой точке, если траектория: а) парабола у = х2;
Решение:
Кривизна плоской кривой: у = f(x) в общем виде определяется по формуле :
![]()
, где - R радиус кривизны в данной точке кривой y’ – первая производная
y’=2 х
y”=2
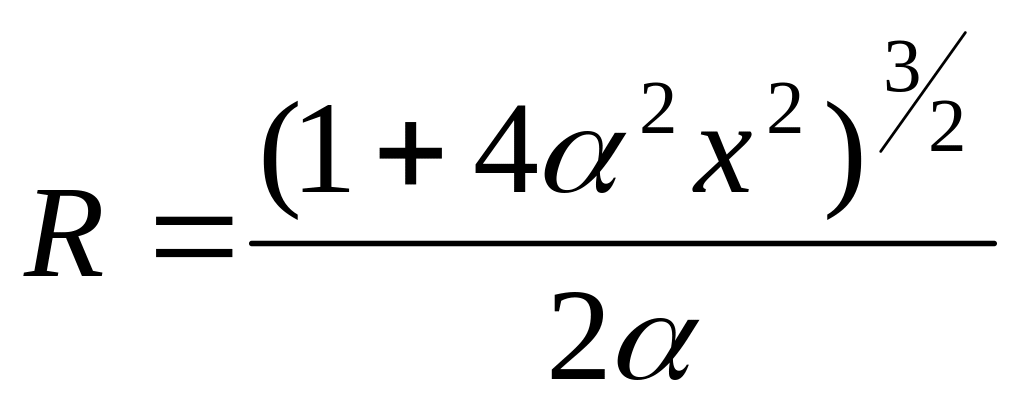 ,R(0)=1/2
,R(0)=1/2
a=v2/R=2v2
Ответ: R(0)=1/2 a=v2/R=2v2 .
Точка движется по плоскости так, что ее тангенциальное ускорение
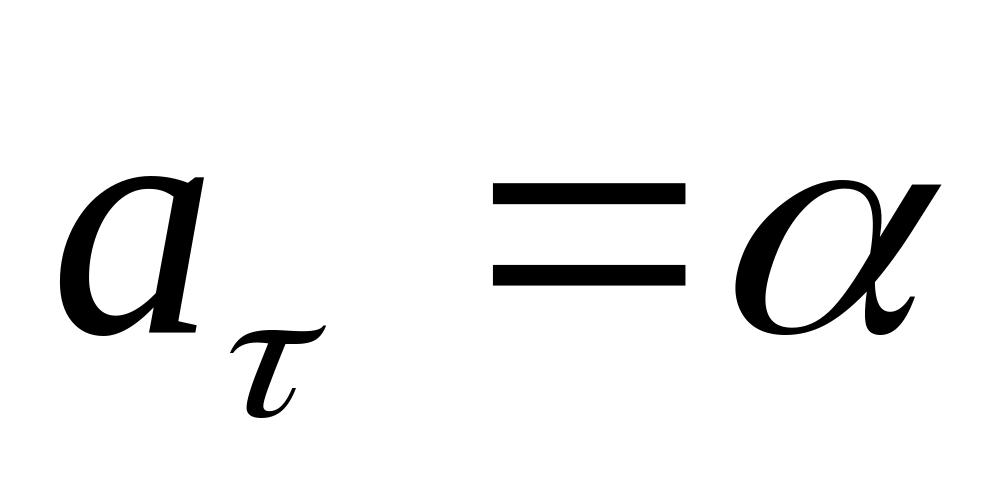 ,
а нормальное ускорение
,
а нормальное ускорение
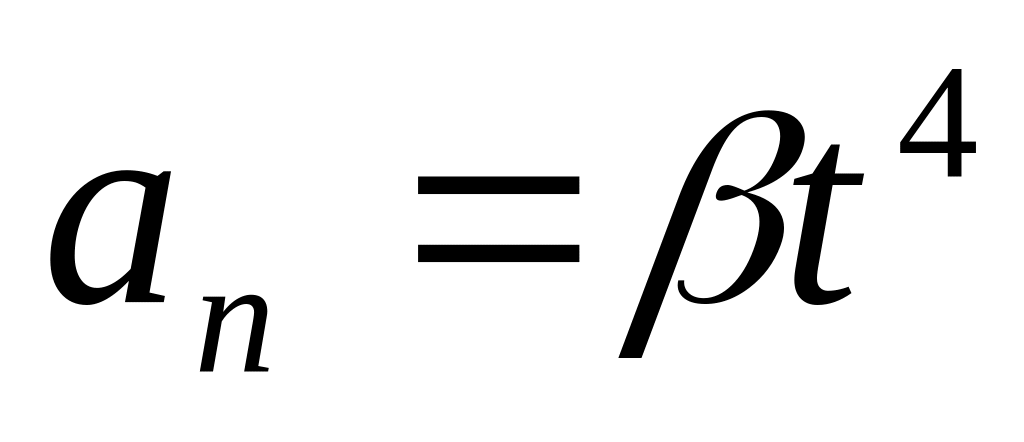 ,
где
и
— положительные постоянные. В момент
,
где
и
— положительные постоянные. В момент
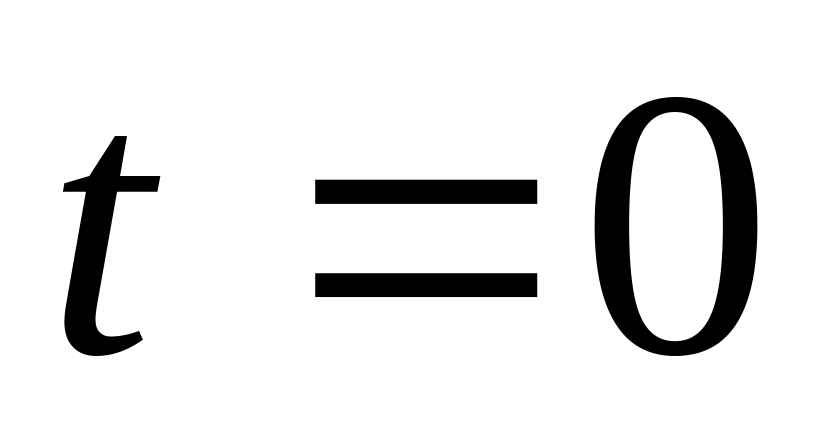 точка покоилась. Найти радиус кривизны
R траектории точки и ее полное ускорение
как функции пройденного пути s.
точка покоилась. Найти радиус кривизны
R траектории точки и ее полное ускорение
как функции пройденного пути s.
Решение:
![]() ,
, ![]() ,
, ![]()
![]()

Ответ:
![]()

Домашняя работа: №№ 1.42(б), 1.44, 1.47. Иродов И.Е. Задачи по общей физики. М.: Бином. Лаб. знаний, 2007
Практическое занятие № 3 «Разложение вектора полного ускорения на нормальную и тангенциальную составляющие. Движение точки по окружности, векторы угловой скорости и углового ускорения»
Закрепление теоретических сведений, результатов лабораторных практикумов и навыков расчета величин в рамках темы «Кинематика механического движения»
Содержание задания:
Предварительная подготовка к рассмотрению темы, заключающая в составление и записи студентами под руководством преподавателя краткого конспекта формул, необходимых для решения задач, которые известны из ранее прошедшего лекционного занятия;
рассмотрение примеров физических явлений, изучаемых в данной теме, приводимых студентами, которые известны из повседневного была, личного опыта, промышленного использования или лабораторных работ.
Решение и обсуждение студентами (индивидуально или триадами) под руководством преподавателя следующих задач:
Точка движется по дуге окружности радиуса R. Ее скорость v~ , где s-пройденный путь. Найти угол между векторами скорости и полного ускорения как функции s.
Решение:
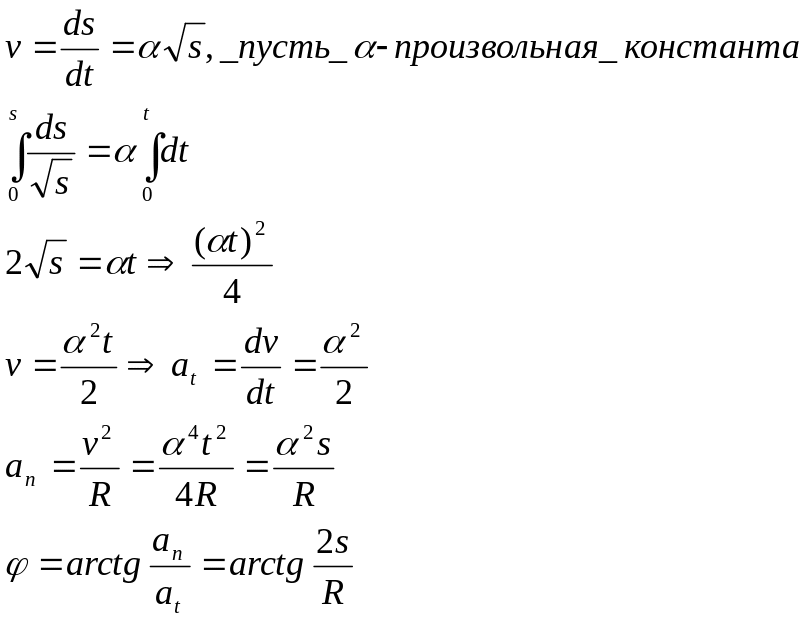

Ответ:
![]()
Твердое тело начинает вращаться вокруг неподвижной оси с угловым ускорением
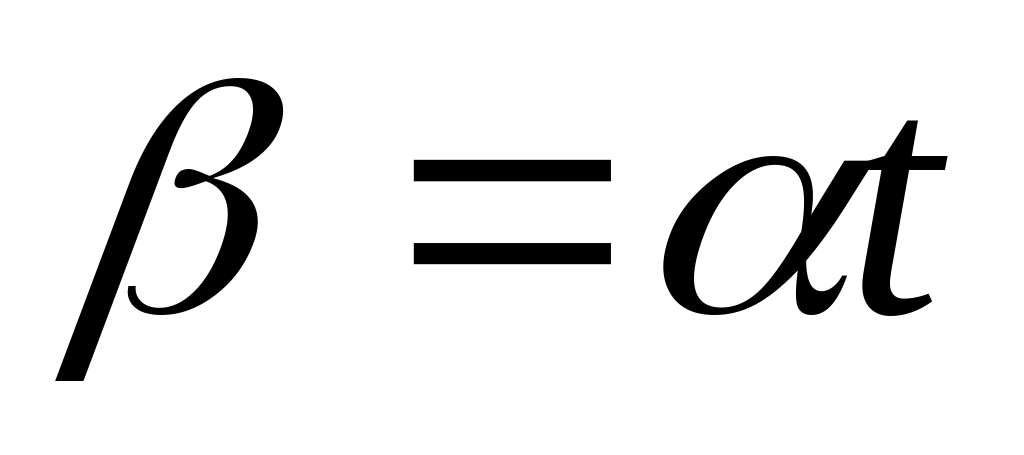 ,
где
,
где
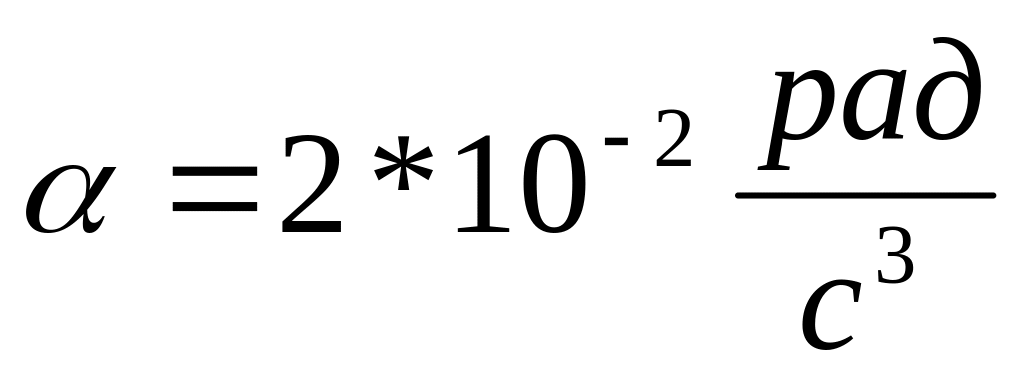 .
Через сколько времени после начала
вращения вектор полного ускорения
произвольной точки тела будет составлять
угол φ=60° с ее вектором скорости?
.
Через сколько времени после начала
вращения вектор полного ускорения
произвольной точки тела будет составлять
угол φ=60° с ее вектором скорости?
Решение:
![]() ,
где
,
где
![]() и
и
![]() ,
,
![]()
![]()
Ответ:
![]()
Твердое тело вращается, замедляясь, вокруг неподвижной оси с угловым ускорением
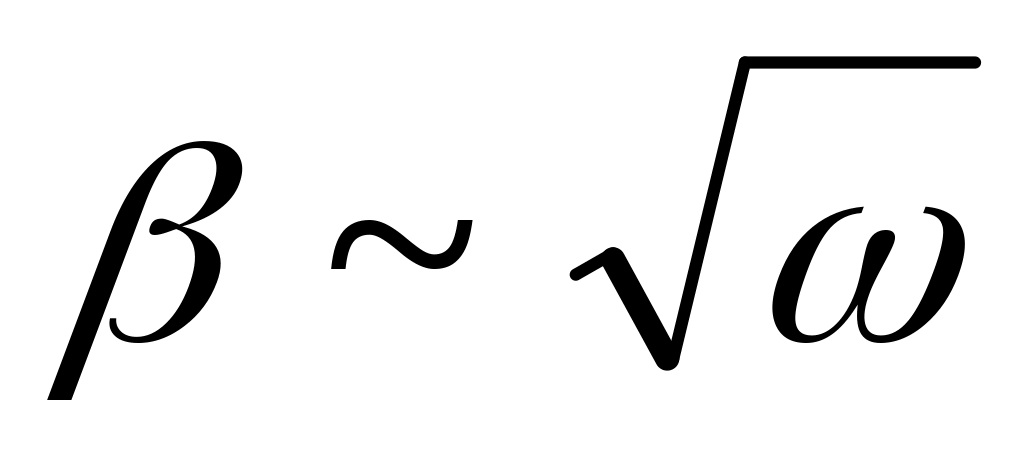 ,
где
,
где
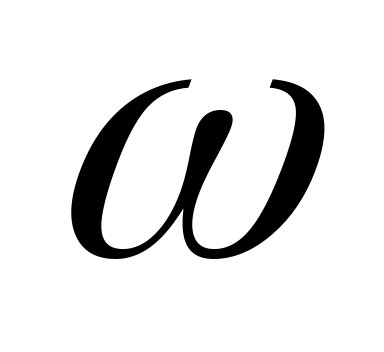 его угловая скорость. Найти среднюю
угловую скорость тела за время, в течение
которого оно будет вращаться, если в
начальный момент его угловая скорость
равна
0.
его угловая скорость. Найти среднюю
угловую скорость тела за время, в течение
которого оно будет вращаться, если в
начальный момент его угловая скорость
равна
0.
Решение:
![]() =--
=--
![]()
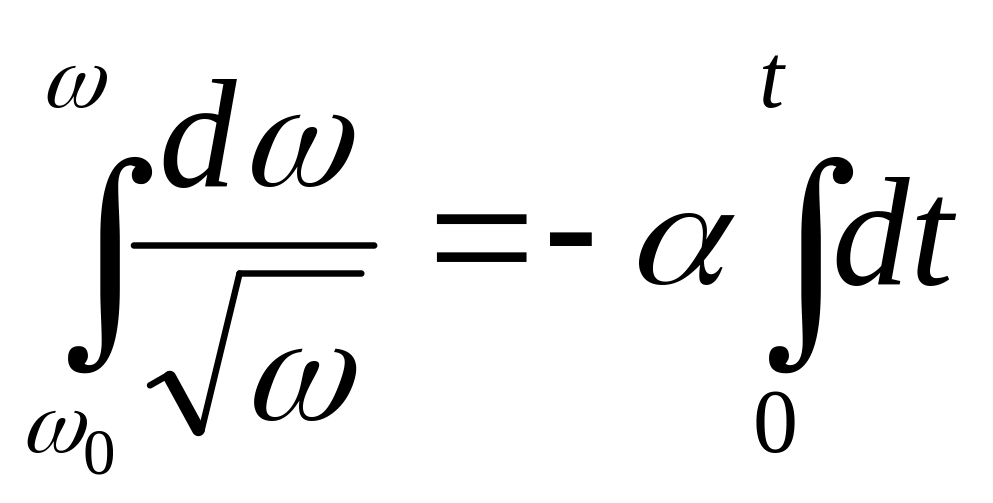
2![]() =
t
(t)=(
=
t
(t)=(![]() -
t/2)2
-
t/2)2
(t)=0
0=(
t)2/4
t=![]() /
/
![]() =
= =
=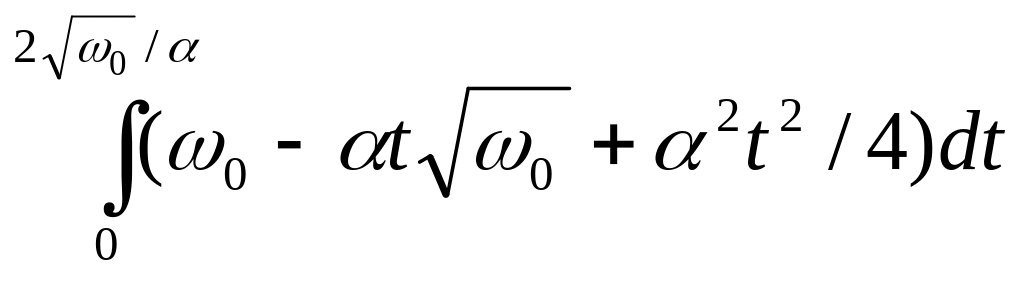 =
=
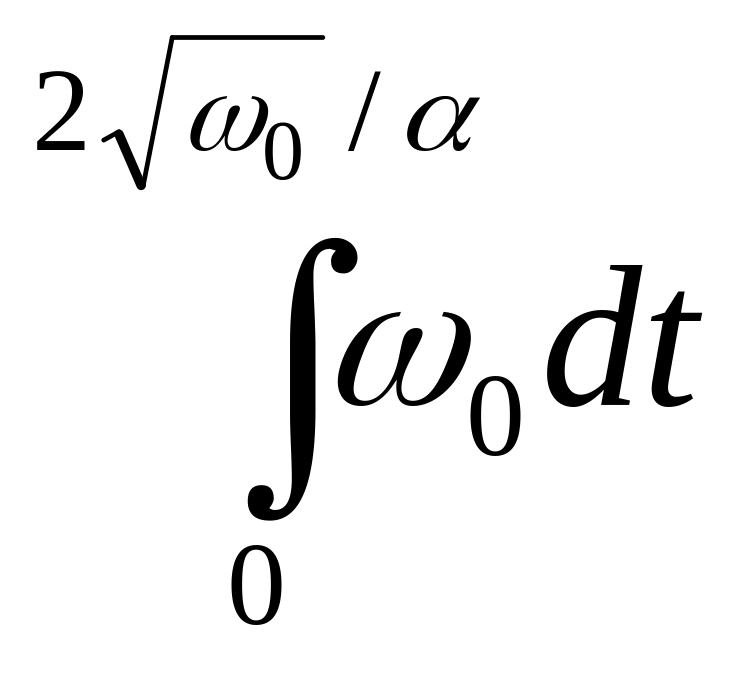 -
-
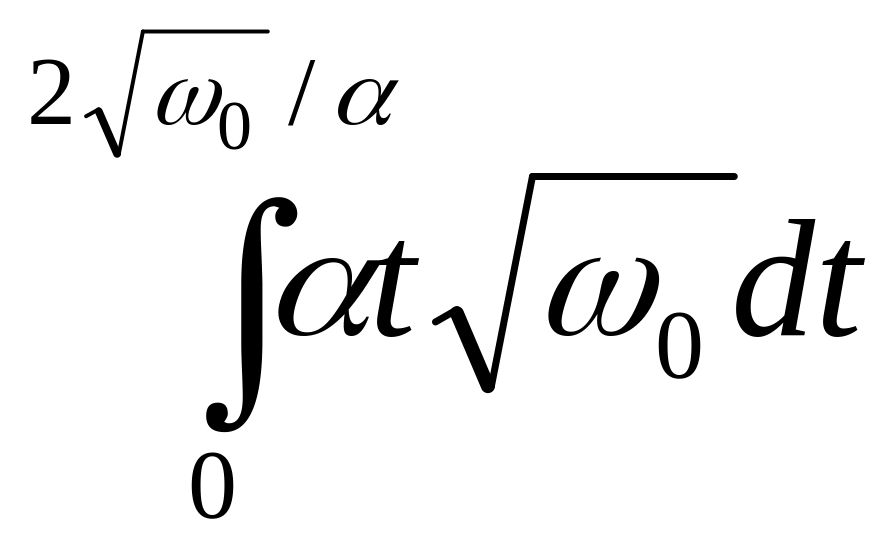 +
+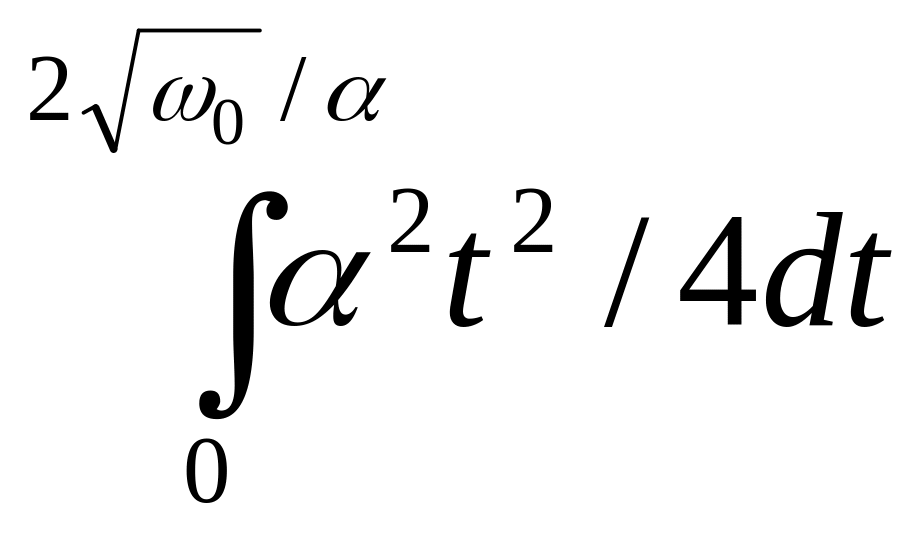 =
=![]() -
+
-
+![]() =
=
<
>=![]() =
0/3
=
0/3
Ответ: < >= 0/3.
Твердое тело вращается с угловой скоростью
 ,
где а=5,0рад/с2,
и
— орты осей х и у. Найти угол а между
векторами углового ускорения
,
где а=5,0рад/с2,
и
— орты осей х и у. Найти угол а между
векторами углового ускорения
 и
и
 в момент, когда
=10,0рад/с2.
в момент, когда
=10,0рад/с2.
Решение:
![]()
![]() ,
,
![]() ,
,
![]()
![]()
![]() ,
,
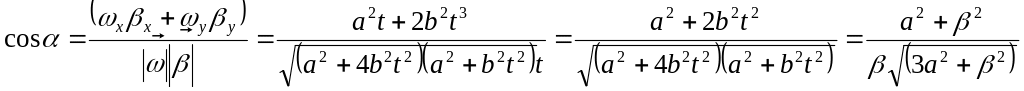
Ответ:
![]()
Домашняя работа: №№ 1.45, 1.50, 1.57, 1.40. Иродов И.Е. Задачи по общей физики. М.: Бином. Лаб. знаний, 2007
Практическое занятие № 4 «Релятивистская механика. Инвариантность длины, интервала времени, ускорения».
Закрепление теоретических сведений, результатов лабораторных практикумов и навыков расчета величин в рамках темы «Релятивистская механика»
Содержание задания:
Предварительная подготовка к рассмотрению темы, заключающая в составление и записи студентами под руководством преподавателя краткого конспекта формул, необходимых для решения задач, которые известны из ранее прошедшего лекционного занятия;
рассмотрение примеров физических явлений, изучаемых в данной теме, приводимых студентами, которые известны из повседневного была, личного опыта, промышленного использования или лабораторных работ.
Решение и обсуждение студентами (индивидуально или триадами) под руководством преподавателя следующих задач:
Стержень движется в продольном направлении с постоянной скоростью относительно инерциальной К – системы отчета. При каком значении длина стержня в этой системе отсчета будет на = 0,5 % меньше его собственной длины?
Решение:
![]() ,
по
условию
,
по
условию
![]()
![]()
![]()
![]()
Ответ:
Имеется прямоугольный треугольник, у которого катет а=5,00м и угол между этим катетом и гипотенузой α=30°. Найти в системе отсчета К', движущейся относительно этого треугольника со скоростью v=0,866с вдоль катета а:
а) соответствующее значение угла α';
б) длину l' гипотенузы и ее отношение к собственной длине.
Решение:
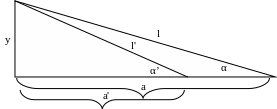
а)
![]() ,
y=y’,
,
y=y’,
![]() ,
и
,
и
![]() ,
,

б)
![]() по теореме Пифагора
по теореме Пифагора
![]() ,
аналогично
,
аналогично
![]()
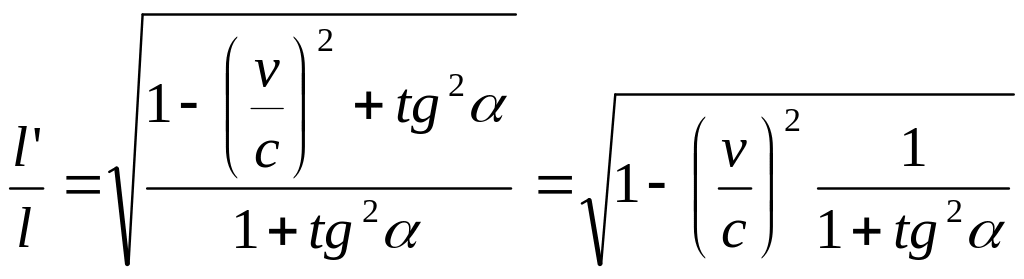
Ответ:
а)
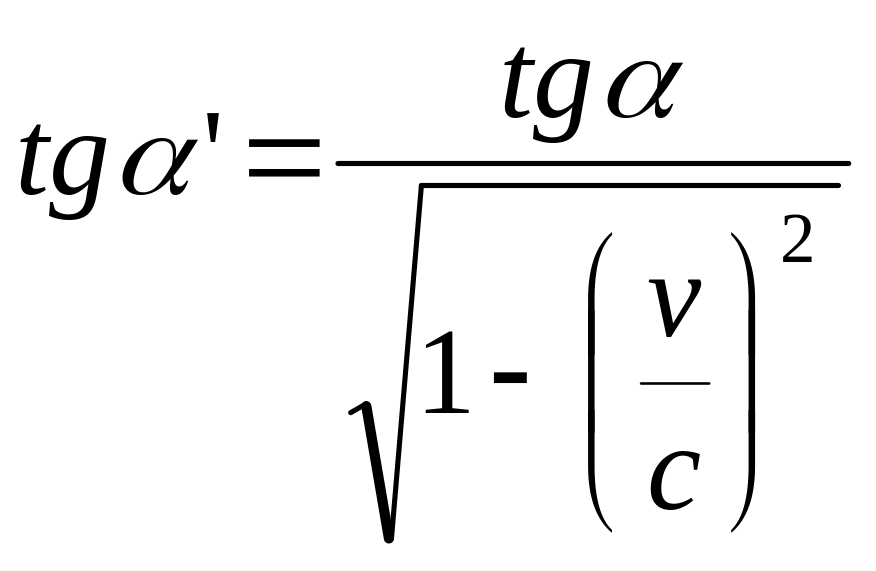 ,
,
![]() .
б)
.
б)
![]() ,
,
![]() .
.
С какой скоростью двигались в К-системе отчета часы, если за время t = 5с (в К - системе) они отстали от часов этой системы на t=0,1с?
Из
закона замедления движущихся часов
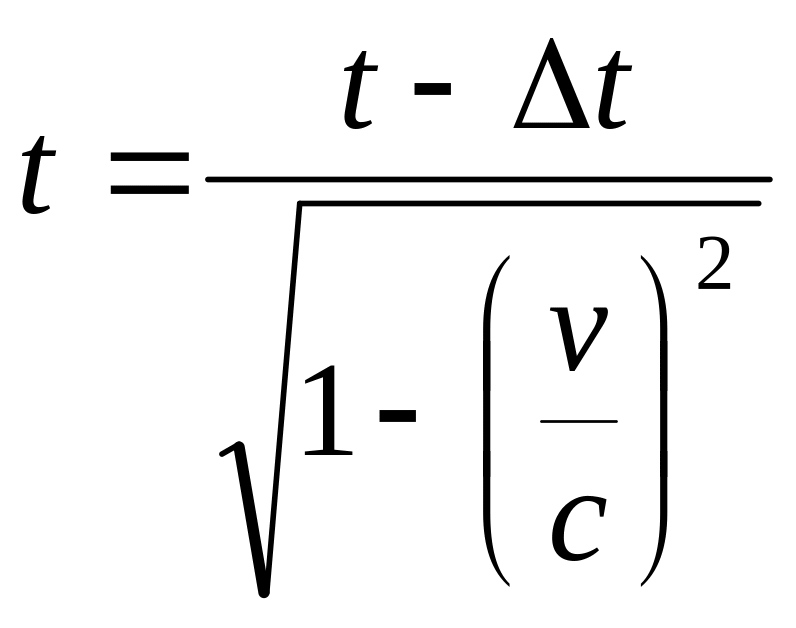 ,
,
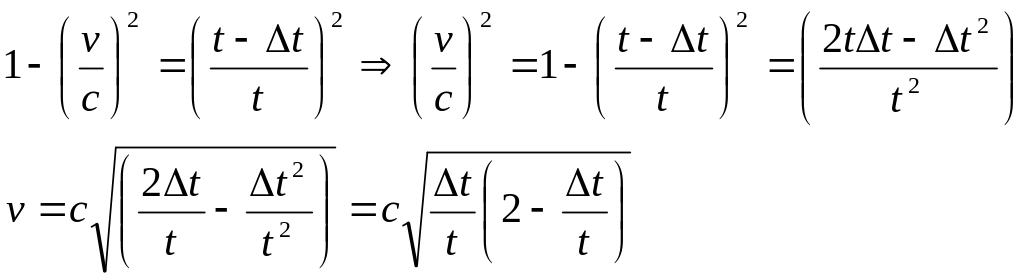
Ответ:
![]()
Домашняя работа: №№ 1.402, 1.403, 1.415. Иродов И.Е. Задачи по общей физики. М.: Бином. Лаб. знаний, 2007
Практическое занятие № 5 «Сокращение длины и изменение формы движущихся тел» -2 часа
Закрепление теоретических сведений, результатов лабораторных практикумов и навыков расчета величин в рамках темы «Релятивистская механика»
Содержание задания:
Предварительная подготовка к рассмотрению темы, заключающая в составление и записи студентами под руководством преподавателя краткого конспекта формул, необходимых для решения задач, которые известны из ранее прошедшего лекционного занятия;
рассмотрение примеров физических явлений, изучаемых в данной теме, приводимых студентами, которые известны из повседневного была, личного опыта, промышленного использования или лабораторных работ.
Решение и обсуждение студентами (индивидуально или триадами) под руководством преподавателя следующих задач:
Во сколько раз релятивистская масса частицы, скорость которой отличается от скорости света на η=0,010 %, превышает ее массу покоя?
Найти скорость, при которой релятивистский импульс частицы в η=1,4 раза превышает ее ньютоновский импульс.
При какой скорости кинетическая энергия частицы равна ее энергии покоя?
Домашняя работа: №№ 1.416, 1.428, 1.440. Иродов И.Е. Задачи по общей физики. М.: Бином. Лаб. знаний, 2007
Практическое занятие № 6 Силы и взаимодействия. Первый, второй законы Ньютона. Третий закон Ньютона
Закрепление теоретических сведений, результатов лабораторных практикумов и навыков расчета величин в рамках темы «Динамика»
Содержание задания:
Предварительная подготовка к рассмотрению темы, заключающая в составление и записи студентами под руководством преподавателя краткого конспекта формул, необходимых для решения задач, которые известны из ранее прошедшего лекционного занятия;
рассмотрение примеров физических явлений, изучаемых в данной теме, приводимых студентами, которые известны из повседневного была, личного опыта, промышленного использования или лабораторных работ.
Решение и обсуждение студентами (индивидуально или триадами) под руководством преподавателя следующих задач.
Решение:
Н
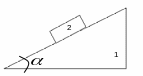 а
горизонтальной поверхности находится
призма 1 массы
а
горизонтальной поверхности находится
призма 1 массы
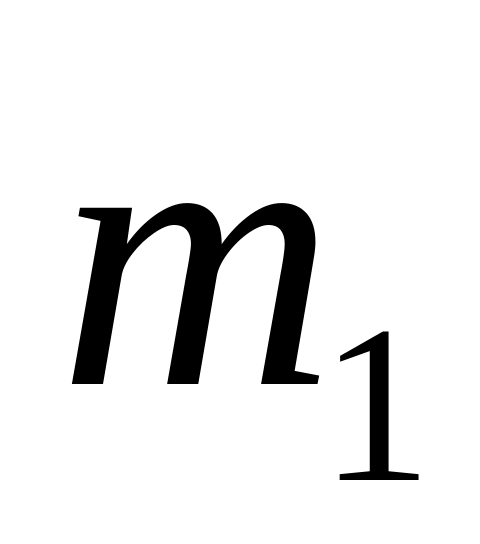 с
углом
(см. рисунок) и на ней брусок 2 массы
с
углом
(см. рисунок) и на ней брусок 2 массы
 .
Пренебрегая трением, найти ускорение
призмы.
.
Пренебрегая трением, найти ускорение
призмы.
Решение:
брусок, соскальзывая будет выдавливать
клин вправо, сообщая ему ускорение
![]() ,
,
![]() - ускорение бруска.
- ускорение бруска.
П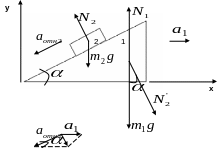 о
второму закону Ньютона
о
второму закону Ньютона
![]()
![]()
![]()
Уравнение проекций:
Ох:![]() (1)
(1)
Оу:![]() (2)
(2)
Ох:
![]() (3)
(3)
Выразим
![]() из (2):
из (2):
![]() и подставим в (1)
и подставим в (1)
![]() (4)
(4)
Выразим
![]() из (4) и подставим в уравнение для клина
(3)
из (4) и подставим в уравнение для клина
(3)
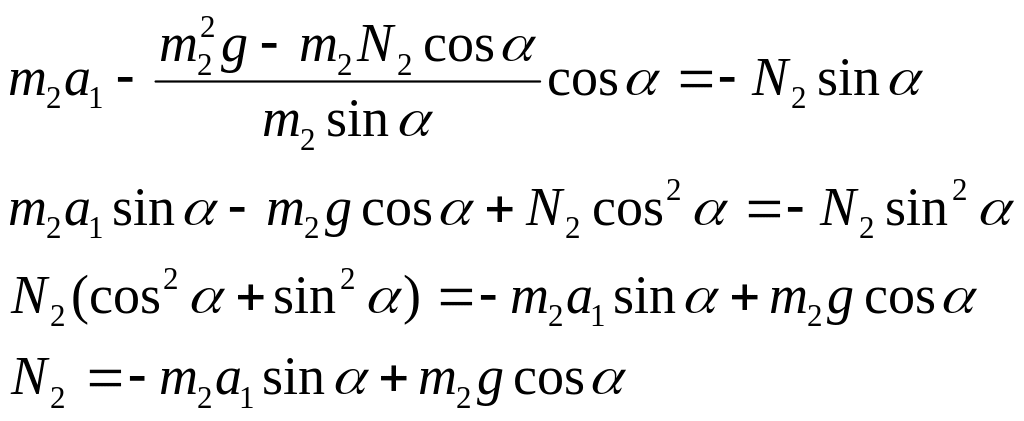
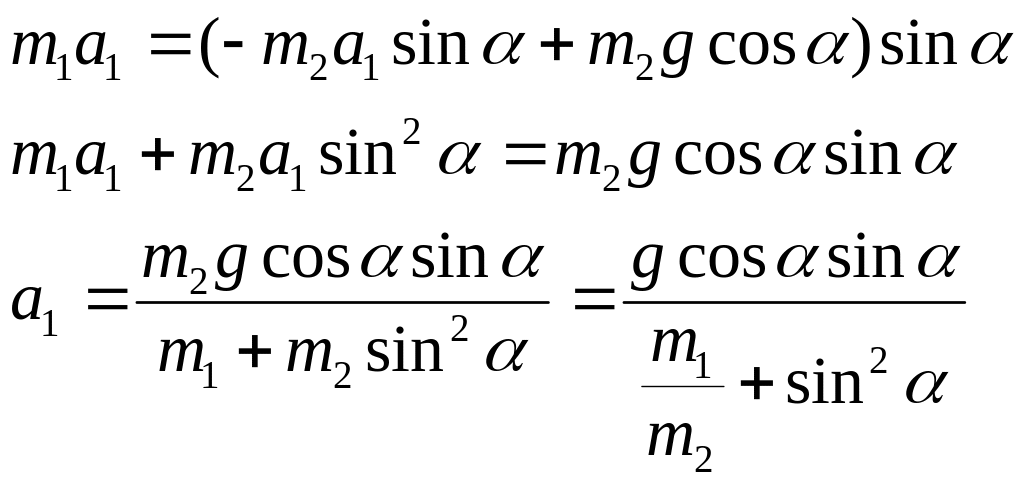
Ответ:
ускорение призмы
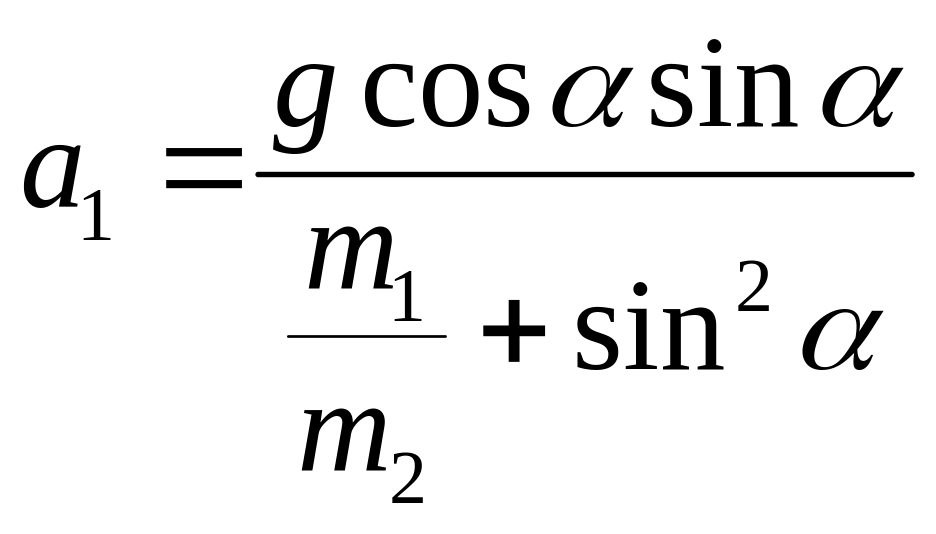 .
.
П
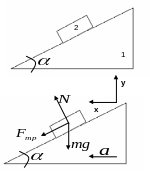 ризме
1, на которой находится брусок 2 массы
ризме
1, на которой находится брусок 2 массы
 ,
сообщили влево горизонтальное ускорение
,
сообщили влево горизонтальное ускорение
 (см. рисунок). При каком максимальном
значении этого ускорения брусок будет
оставаться еще неподвижным относительно
призмы, если коэффициент трения между
ними
(см. рисунок). При каком максимальном
значении этого ускорения брусок будет
оставаться еще неподвижным относительно
призмы, если коэффициент трения между
ними
 ?
?
Решение:
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
Подставим (3) в (2)
![]()
![]() (4)
(4)
Разделим (1) на (4)
![]()
![]()
Ответ:
![]()
С
 амолет
делает «мертвую петлю»
амолет
делает «мертвую петлю»
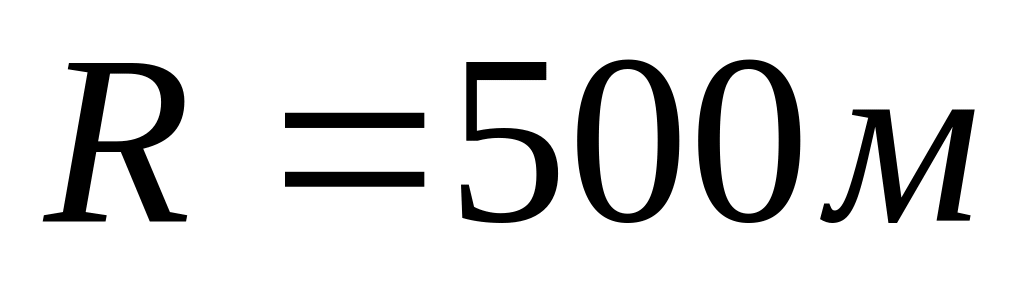 со скоростью
со скоростью
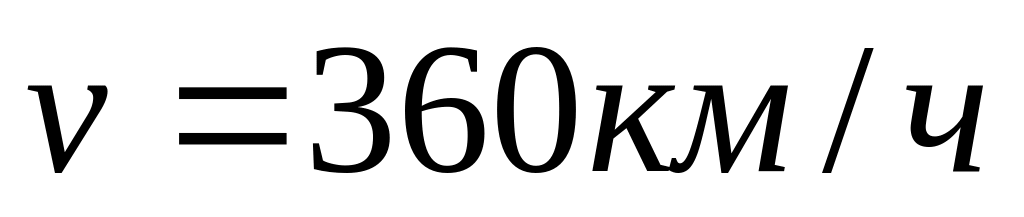 .
Найти вес летчика массы
.
Найти вес летчика массы
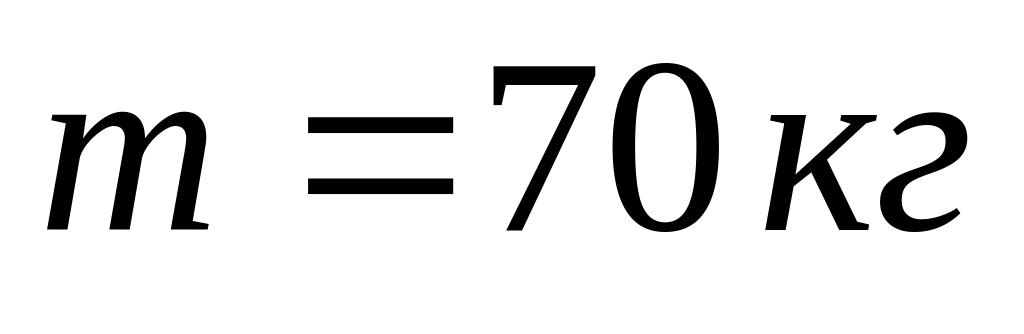 в нижней, верхней и средней точках
петли.
в нижней, верхней и средней точках
петли.
Решение:
В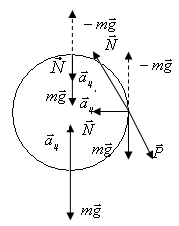 каждой точке на тело действуют силы
тяжести (
каждой точке на тело действуют силы
тяжести (![]() ),
реакции опоры (
),
реакции опоры (![]() ),
центростремительная сила
(
),
центростремительная сила
(![]() ).Центростремительная
сила (
)
направлена к центру окружности, по
радиусу; сила тяжести (
)
вертикально вниз, для определения
направления реакции опоры запишем
второй закон Ньютона.
).Центростремительная
сила (
)
направлена к центру окружности, по
радиусу; сила тяжести (
)
вертикально вниз, для определения
направления реакции опоры запишем
второй закон Ньютона.
Для
верхней точки:
![]() ,
все три силы направлены по радиусу к
центру окружности. Тогда
,
все три силы направлены по радиусу к
центру окружности. Тогда
![]() ,
где
,
где
![]() и
и
![]() .
.
Для
средней точки:
![]() ,
,
![]() .
.
Для
нижней точки:
![]() ,
все три силы направлены по радиусу к
центру окружности. Тогда
,
все три силы направлены по радиусу к
центру окружности. Тогда
![]() ,
где
и
.
,
где
и
.
Ответ:
для верхней точки:
![]() ,
средней точки:
,
средней точки:![]() ,
нижней точки
,
нижней точки
![]() .
.
На покоившуюся частицу массы в момент
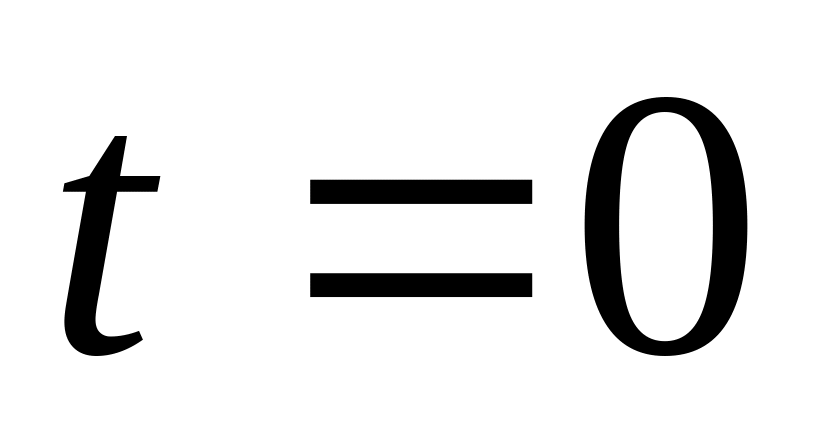 начала
действовать сила, зависящая от времени
по закону
начала
действовать сила, зависящая от времени
по закону
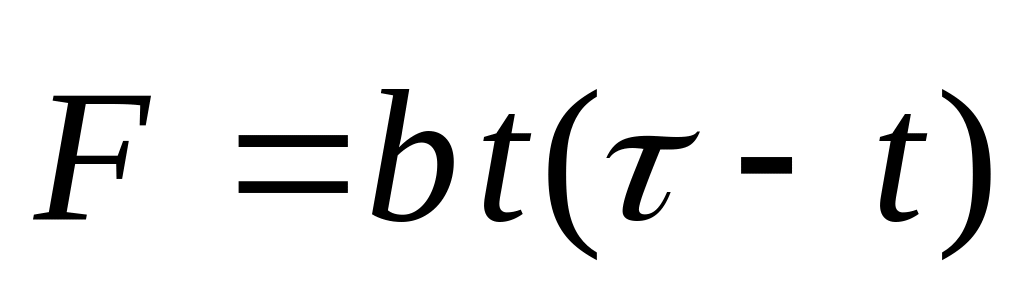 ,
где
,
где
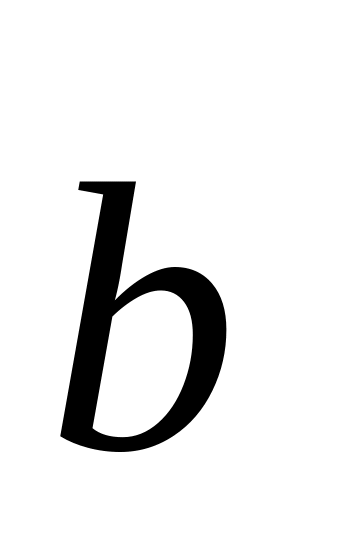 - постоянный вектор,
- постоянный вектор,
 - время, в течение которого действует
данная сила.
- время, в течение которого действует
данная сила.
Найти:
Импульс частицы после окончания действия силы;
Путь, пройденный частицей за время действия силы.
Решение:
Сила, действующая на тело, равна изменению импульса с течением времени
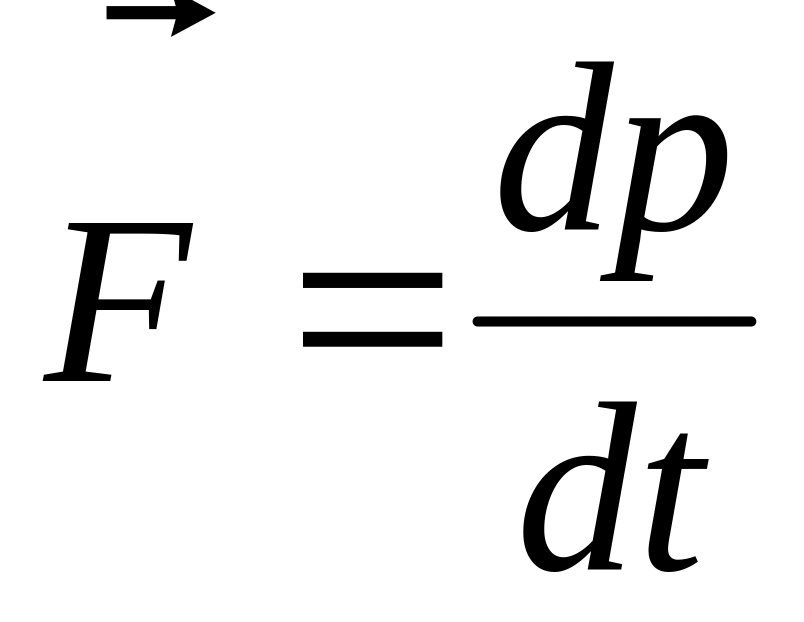 .
Тогда
.
Тогда
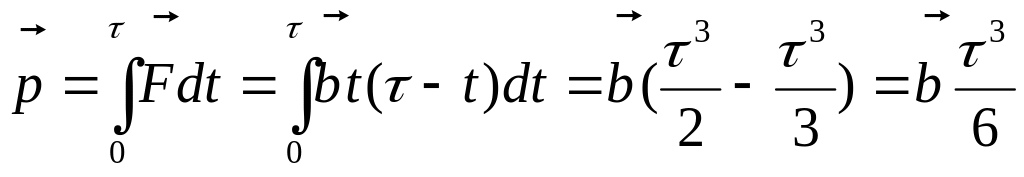 .
.Импульс по определению равен
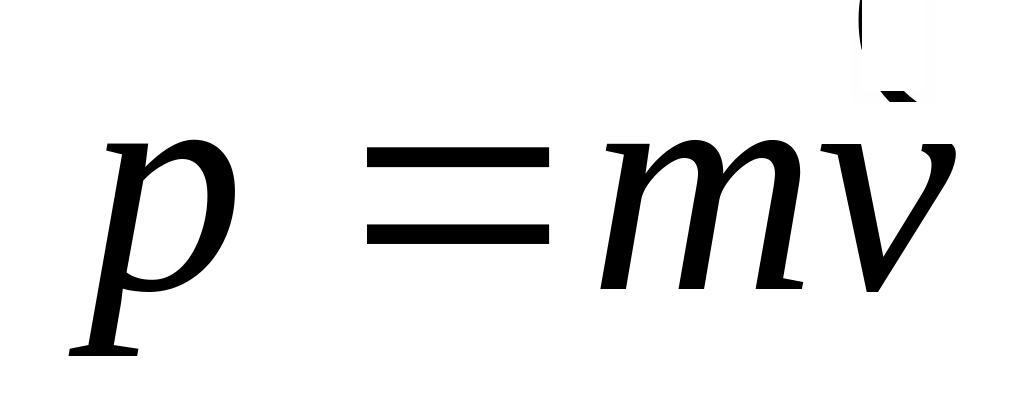 ,
а скорость можно записать как
,
а скорость можно записать как
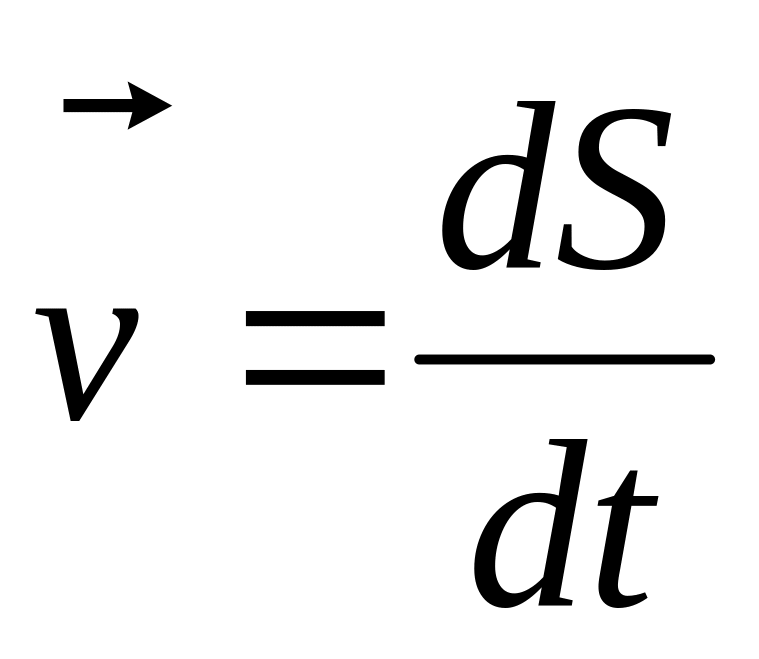 .
Тогда действующая сила
.
Тогда действующая сила
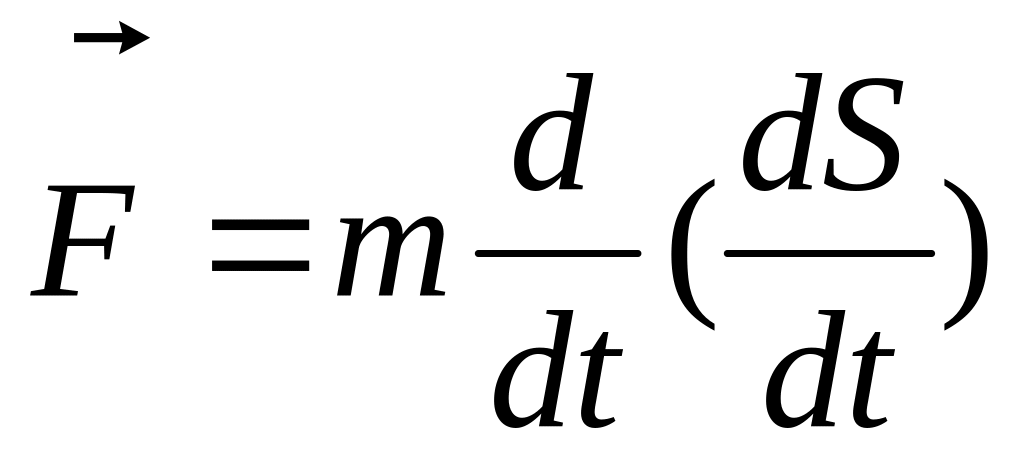 .
Проинтегрируем это выражение по времени
два раза.
.
Проинтегрируем это выражение по времени
два раза.
![]()
Ответ:
![]() и
и
![]()
Частица массы в момент начинает двигаться под действием силы,
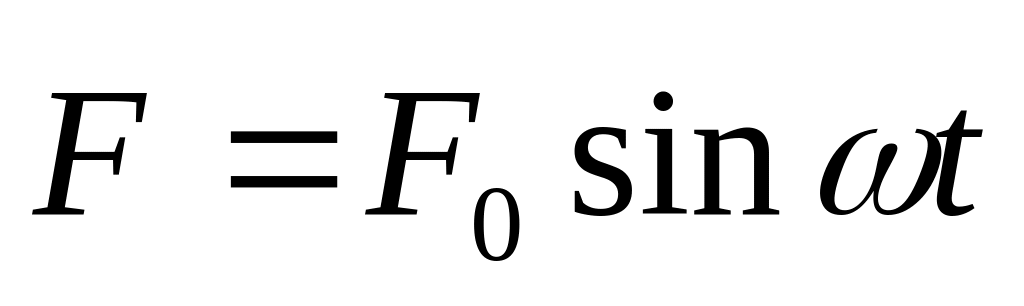 ,
где
,
где
 и
-
постоянные. Найти
путь, пройденный частицей, в зависимости
от
и
-
постоянные. Найти
путь, пройденный частицей, в зависимости
от
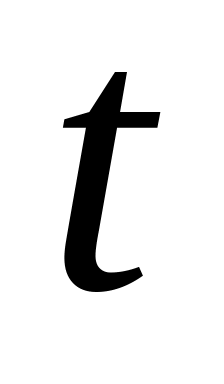 .
Изобразить примерный график этой
зависимости.
.
Изобразить примерный график этой
зависимости.
Решение:
Сила,
действующая на тело, равна изменению
импульса с течением времени
.
Импульс по определению равен
![]() ,
а скорость можно записать как
.
Тогда действующая сила
.
Проинтегрируем это выражение по времени
два раза.
,
а скорость можно записать как
.
Тогда действующая сила
.
Проинтегрируем это выражение по времени
два раза.
![]() .
Интегрируя первый раз, получаем
.
Интегрируя первый раз, получаем
![]() .
.
В
итоге получаем, что путь
![]() .
.
Ответ:
.
График
![]()

В момент частица массы начинает двигаться под действием силы,
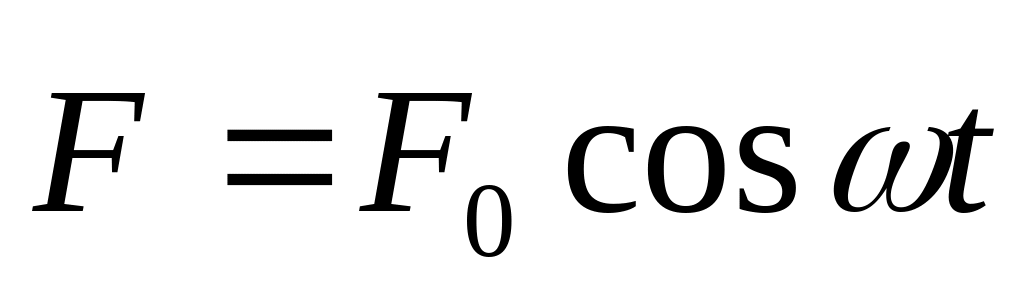 ,
где
,
где
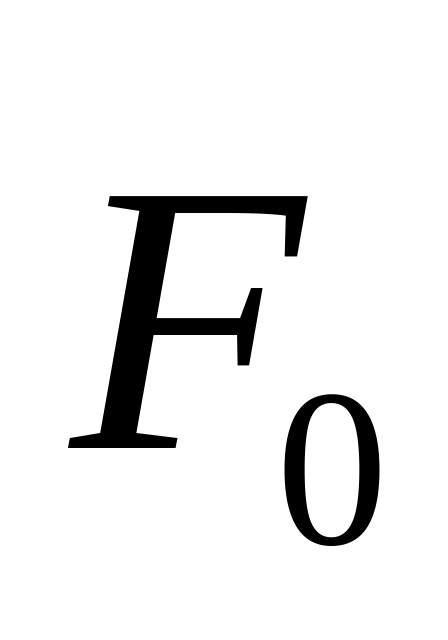 и
-
постоянные. Сколько
времени частица будет двигаться до
первой остановки? Какой путь она пройдет
за это время? Какова максимальная
скорость частицы на этом пути?
и
-
постоянные. Сколько
времени частица будет двигаться до
первой остановки? Какой путь она пройдет
за это время? Какова максимальная
скорость частицы на этом пути?
Решение:
Сила,
действующая на тело, равна изменению
импульса с течением времени
.
Импульс по определению равен
.
Тогда действующая сила
![]() .
Отсюда скорость равна
.
Отсюда скорость равна
![]() .
Скорость в точке остановке равна нулю,
тогда получаем
.
Скорость в точке остановке равна нулю,
тогда получаем
![]() ,
и время равно
,
и время равно
![]() (
(![]() ,
,
![]() ).
А путь, пройденный точкой за это время
).
А путь, пройденный точкой за это время
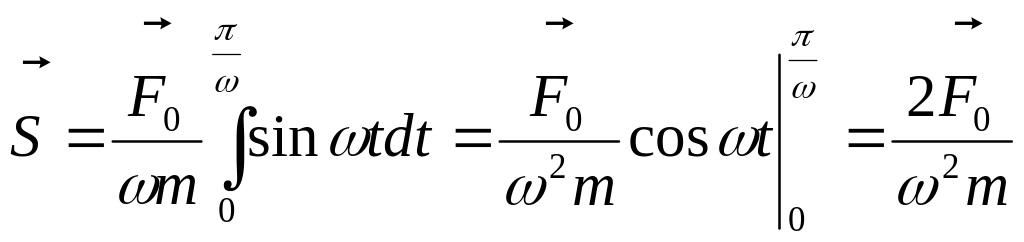 .
.
Скорость
частицы
![]() ,
продифференцируем это выражение по
времени и приравняем его к нулю.
,
продифференцируем это выражение по
времени и приравняем его к нулю.
![]() ,
отсюда
,
отсюда
![]() ,
значит
,
значит
![]()
Тогда
![]() .
.
Ответ:
,
![]() ,
,
Домашняя работа: №№ 1.59, 1.61, 1.105, 1.95. Иродов И.Е. Задачи по общей физики. М.: Бином. Лаб. знаний, 2007
Практическое занятие № 7 «Понятие импульса тела, импульса силы; момента импульса, момента силы. Уравнение моментов»
Закрепление теоретических сведений, результатов лабораторных практикумов и навыков расчета величин в рамках темы «Динамика»
Содержание задания:
Предварительная подготовка к рассмотрению темы, заключающая в составление и записи студентами под руководством преподавателя краткого конспекта формул, необходимых для решения задач, которые известны из ранее прошедшего лекционного занятия;
рассмотрение примеров физических явлений, изучаемых в данной теме, приводимых студентами, которые известны из повседневного была, личного опыта, промышленного использования или лабораторных работ.
Решение и обсуждение студентами (индивидуально или триадами) под руководством преподавателя следующих задач:
Снаряд, выпущенный со скоростью
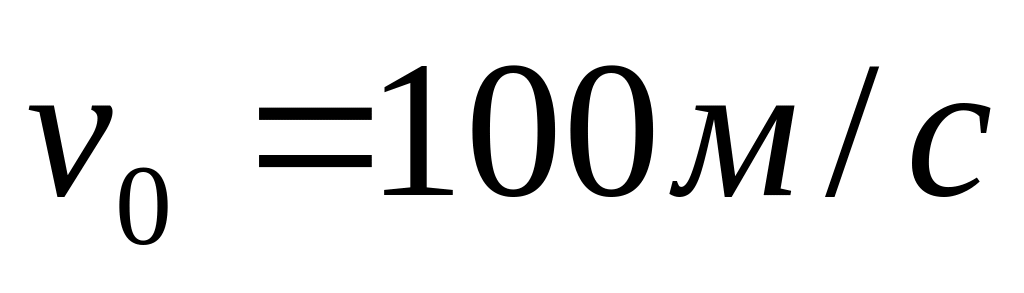 под углом
под углом
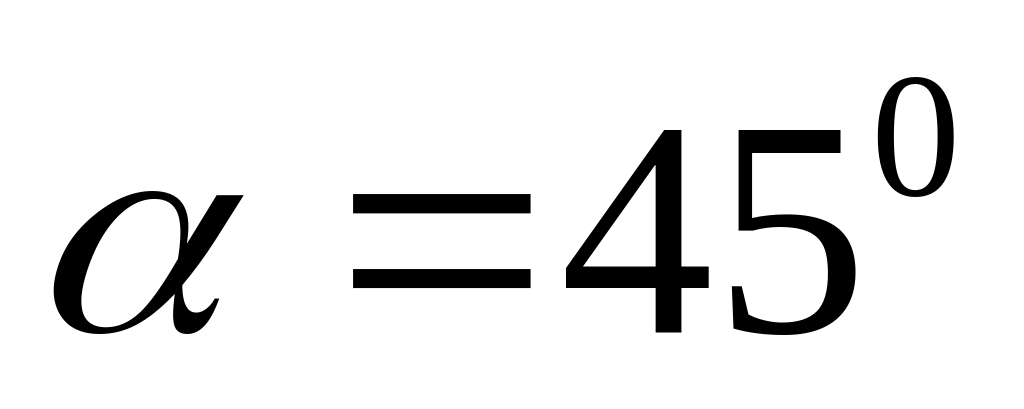 к горизонту, разорвался в верхней точке
O траектории на два одинаковых осколка.
Один осколок упал на землю под точкой
O со скоростью,
к горизонту, разорвался в верхней точке
O траектории на два одинаковых осколка.
Один осколок упал на землю под точкой
O со скоростью,
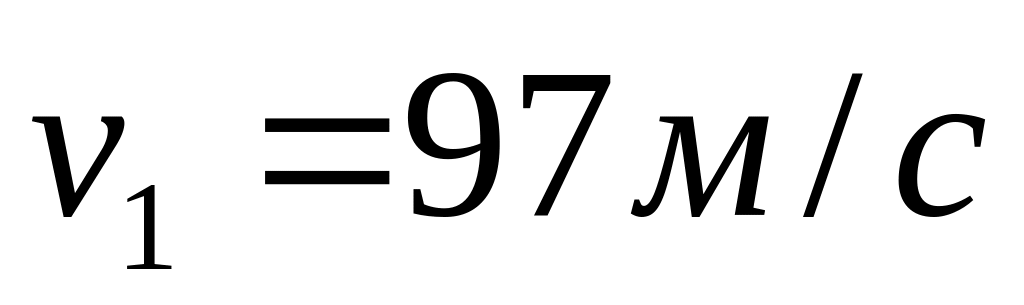 .
С какой скоростью упал на землю второй
осколок? Сопротивления воздуха нет.
.
С какой скоростью упал на землю второй
осколок? Сопротивления воздуха нет.
Решение:
Закон
сохранения энергии для первого осколка
![]() (1)
(1)
Закон
сохранения энергии для второго осколка
![]() (2)
(2)
Закон
сохранения импульса
![]() (3)
(3)
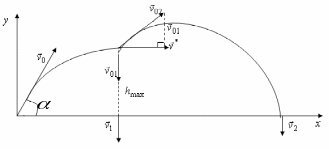
Из
треугольника, указанного на рисунке
![]() (4)
(4)
Выразим
из (1)
![]() :
:
![]()
![]()
 можно
найти из уравнения движения для снаряда
(проекция уравнения на ось Oy):
можно
найти из уравнения движения для снаряда
(проекция уравнения на ось Oy):
![]()
Тогда
![]() (5), также из уравнения движения (проекция
на ось Ox):
(5), также из уравнения движения (проекция
на ось Ox):
![]() .
.
Определим
![]() из (4), зная, что
из (4), зная, что
![]() и
и
![]() .
.
![]() .
.
И
теперь из (2) найдем
![]() .
.
![]()
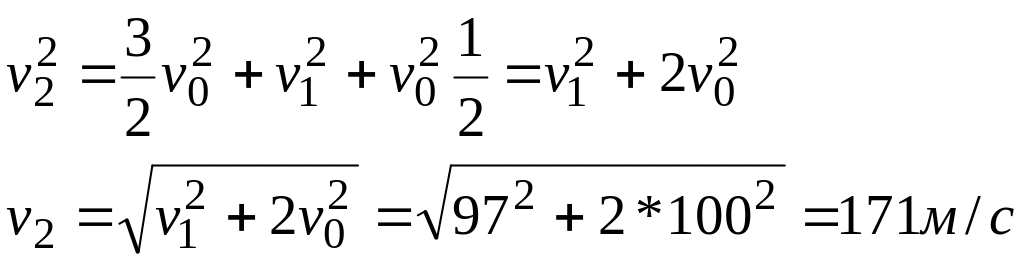
Ответ:
![]()
Плот массы
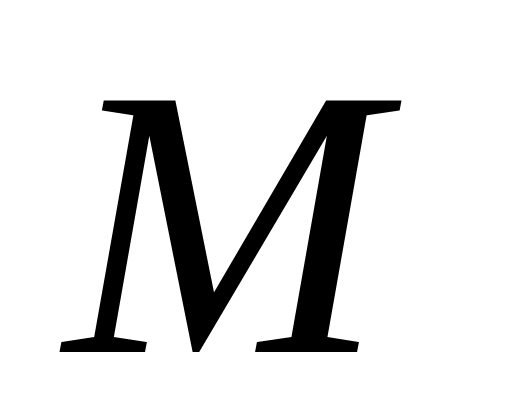 с
находящимся на нем человеком массы
неподвижно стоит на поверхности пруда.
Относительно плота человек совершает
перемещение
с
находящимся на нем человеком массы
неподвижно стоит на поверхности пруда.
Относительно плота человек совершает
перемещение
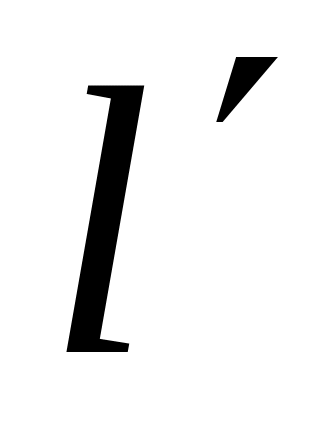 со скоростью
со скоростью
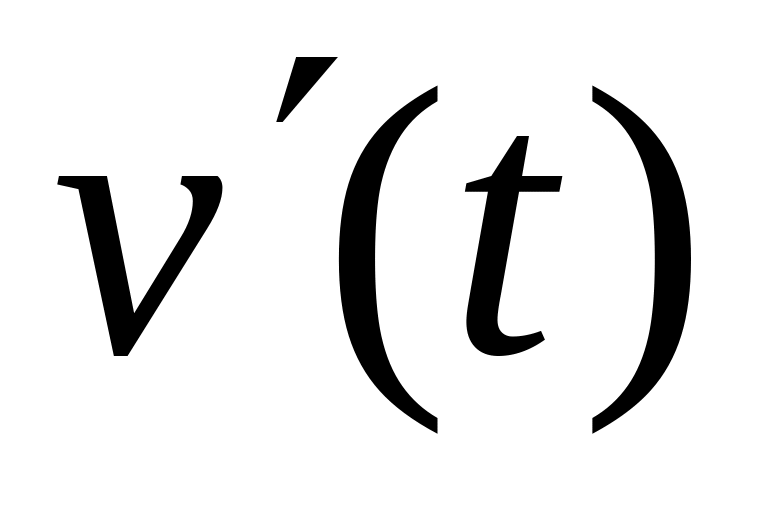 и останавливается. Пренебрегая
сопротивлением воды, найти:
и останавливается. Пренебрегая
сопротивлением воды, найти:
перемещение
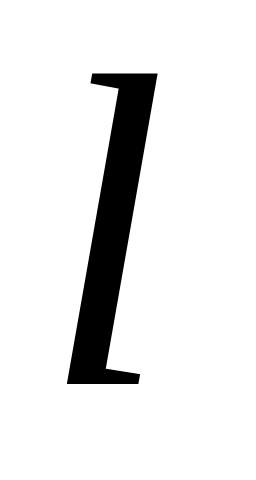 плота относительно берега;
плота относительно берега;горизонтальную составляющую силы, с которой человек действовал на плот в процессе движения.
Решение:
Так как сопротивление движению плота в воде пренебрежимо мало, то сумма внешних сил, действующих на замкнутую систему «человек-плот» равна нулю
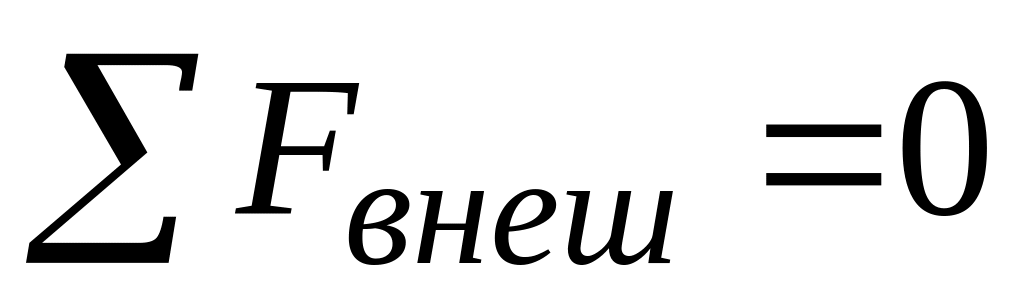 .
.
Положение центра масс системы будет неизменно, что и наблюдается на берегу.
![]() ,
т.к.
,
т.к.
![]() .
.
![]()
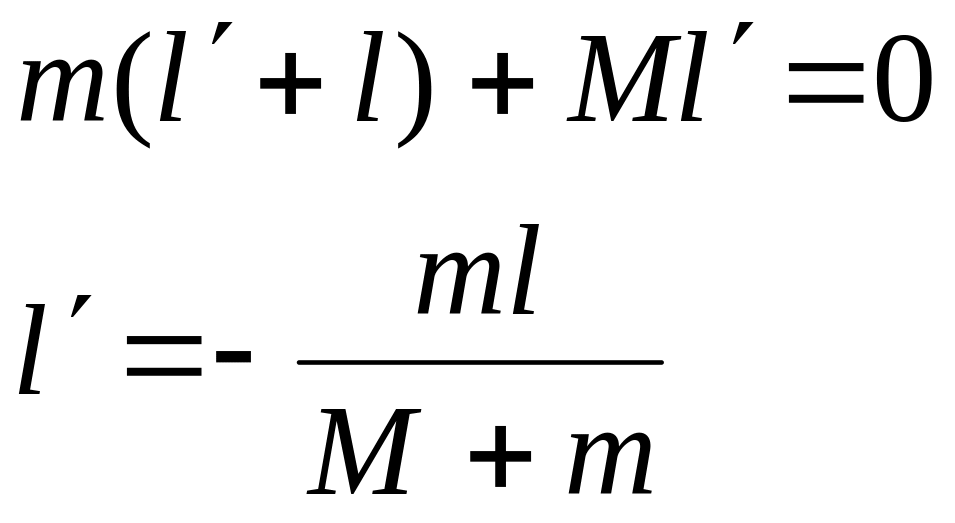
Горизонтальная составляющая силы

![]() -
скорость плота, можно определить из
закона сохранения импульса
-
скорость плота, можно определить из
закона сохранения импульса
![]()
Тогда
![]() и
и
![]() .
.
Ответ:
а)
![]() ;
б)
.
;
б)
.
Ц
 епочка
епочка
 длины
длины
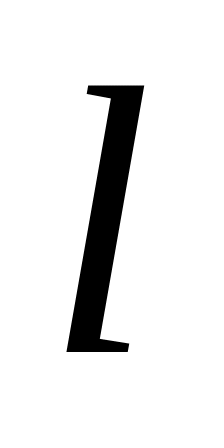 находится в гладкой горизонтальной
трубке, так что часть ее длины
находится в гладкой горизонтальной
трубке, так что часть ее длины
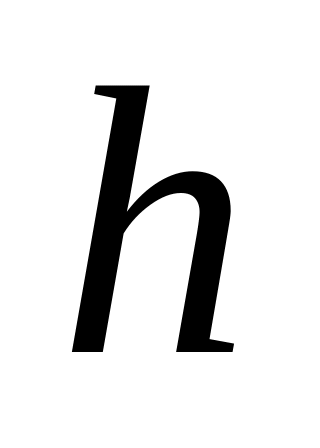 свободно свешивается, касаясь своим
концом
свободно свешивается, касаясь своим
концом
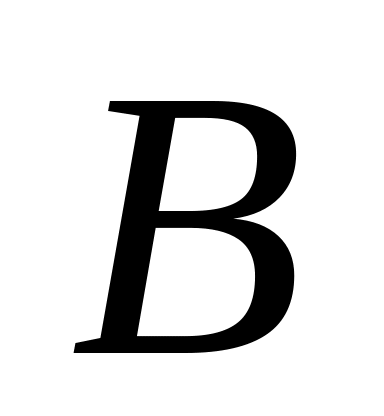 поверхности стола (рис. 1.138). В некоторый
момент конец
поверхности стола (рис. 1.138). В некоторый
момент конец
 цепочки отпустили. С какой скоростью
он выскочит из трубки?
цепочки отпустили. С какой скоростью
он выскочит из трубки?
Решение:
Н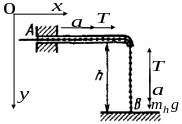 а
участок цепочки, находящийся в трубке
действуют силы:
а
участок цепочки, находящийся в трубке
действуют силы:
![]() - сила натяжения,
- сила натяжения,
![]() - сила тяжести, направленная вертикально
вниз и
- сила тяжести, направленная вертикально
вниз и
![]() - реакция опоры, направленная противоположно
силе тяжести.
- реакция опоры, направленная противоположно
силе тяжести.
Сумма действующих сил по второму закону Ньютона равна произведению массы на сообщаемое ускорение:
![]() (1)
(1)
Введем
систему координат как указано на рисунке.
Проекция уравнения (1) на ось Оx:
![]() (2). Масса горизонтального участка цепочки
равна
(2). Масса горизонтального участка цепочки
равна
![]() ,
где
,
где
![]() - линейная плотность. Проведем аналогичные
рассуждения и для вертикального участка
цепочки:
- линейная плотность. Проведем аналогичные
рассуждения и для вертикального участка
цепочки:
![]() .
.
Проекция
на ось Оy
запишется как
![]() (3), где
(3), где
![]() .
.
Подставим
(2) в (3):
![]()
![]() ,
отсюда
,
отсюда
![]() (3).
(3).
Ускорение
характеризует быстроту изменения
скорости и определяется как
![]() ,
помножим числитель и знаменатель на
,
помножим числитель и знаменатель на
![]() :
:
![]() (4).
(4).
![]() ,
так как со временем падения цепочки
длина горизонтального участка уменьшается.
,
так как со временем падения цепочки
длина горизонтального участка уменьшается.
Подставим
выражение (3) в (4)
![]() и
проинтегрируем.
и
проинтегрируем.
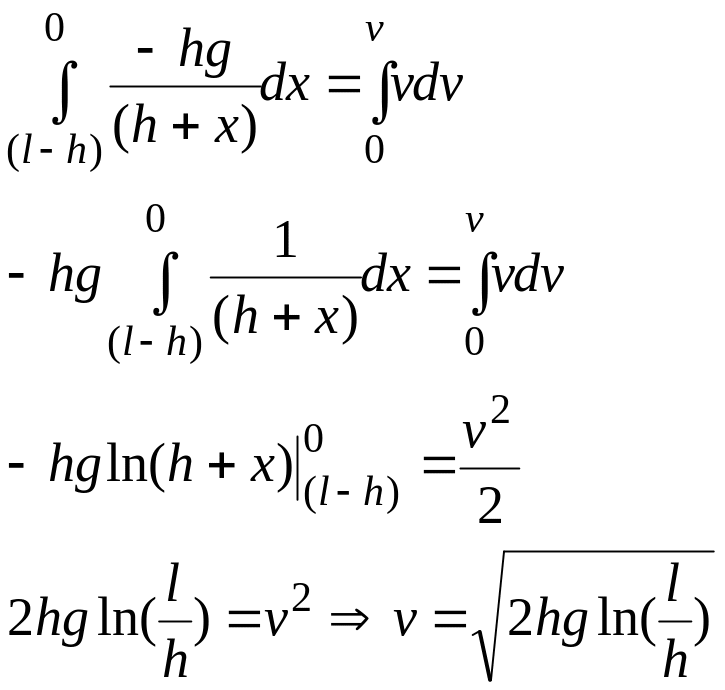
Ответ:
![]() .
.
Домашняя работа: №№ 1.127, 1.125, 1.129, 1.132. Иродов И.Е. Задачи по общей физики. М.: Бином. Лаб. знаний, 2007
Практическое занятие № 8 «Система материальных точек, ее импульс, уравнение моментов для системы материальных точек. Центр масс»
Закрепление теоретических сведений, результатов лабораторных практикумов и навыков расчета величин в рамках темы «Динамика»
Содержание задания:
Предварительная подготовка к рассмотрению темы, заключающая в составление и записи студентами под руководством преподавателя краткого конспекта формул, необходимых для решения задач, которые известны из ранее прошедшего лекционного занятия;
рассмотрение примеров физических явлений, изучаемых в данной теме, приводимых студентами, которые известны из повседневного была, личного опыта, промышленного использования или лабораторных работ.
Решение и обсуждение студентами (индивидуально или триадами) под руководством преподавателя следующих задач:
Во время ловли рыбы, рыбаки решили поменяться местами в лодке. Насколько переместится лодка относительно воды? Масса лодки
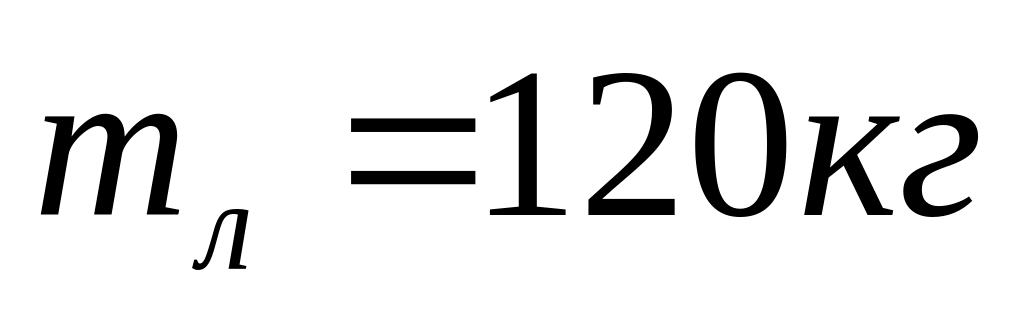 ,
длина лодки
,
длина лодки
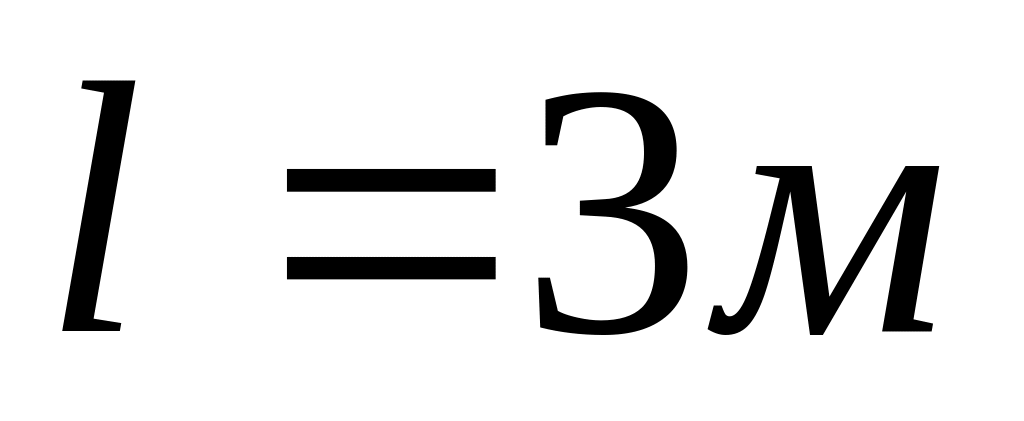 .
Массы рыбаков
.
Массы рыбаков
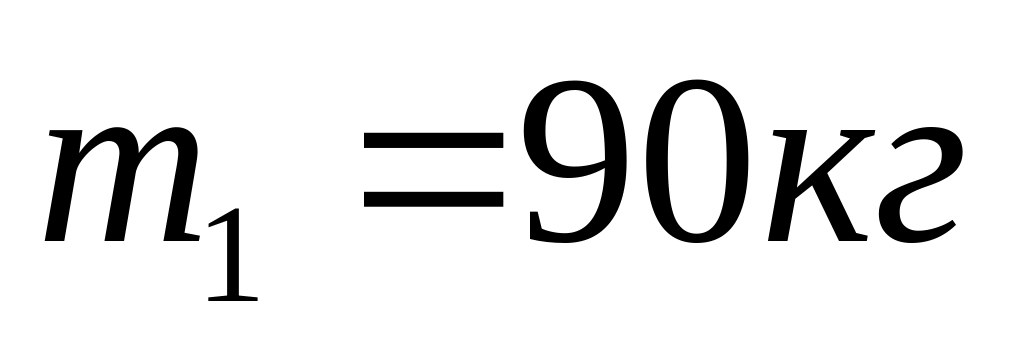 и
и
 .
.
Решение:
По закону сохранения изменения импульса в системе равно нулю.
![]() (1)
(1)
где
![]() - скорость центр масс системы.
- скорость центр масс системы.
Из
(1)
![]() или если система покоится
или если система покоится
![]() .
.
Радиус
центра масс величина постоянная
![]()
![]() -
радиус центра масс системы до перемещения
рыбаков.
-
радиус центра масс системы до перемещения
рыбаков.
![]() -
радиус центра масс системы после
перемещения рыбаков.
-
радиус центра масс системы после
перемещения рыбаков.

Ответ:
![]() .
.
Через блок, укрепленный на потолке комнаты, перекинута нить, на концах которой подвешены тела масс m1и m2. Массы блока и нити пренебрежимо малы, трения нет. Найти ускорение центра масс этой системы.
Практическое занятие № 9 Работа силы. Кинетическая энергия
Закрепление теоретических сведений, результатов лабораторных практикумов и навыков расчета величин в рамках темы «Динамика»
Содержание задания:
Предварительная подготовка к рассмотрению темы, заключающая в составление и записи студентами под руководством преподавателя краткого конспекта формул, необходимых для решения задач, которые известны из ранее прошедшего лекционного занятия;
рассмотрение примеров физических явлений, изучаемых в данной теме, приводимых студентами, которые известны из повседневного была, личного опыта, промышленного использования или лабораторных работ.
Решение и обсуждение студентами (индивидуально или триадами) под руководством преподавателя следующих задач:
Частица совершила перемещение по некоторой траектории в плоскости ху из точки 1 с радиусом-вектором
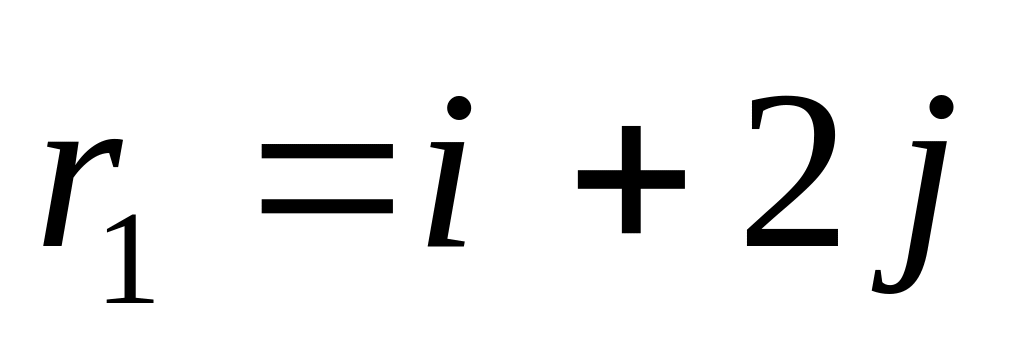 в точку 2 с радиусом-вектором
в точку 2 с радиусом-вектором
 .
При этом на нее действовали некоторые
силы, одна из которых
.
При этом на нее действовали некоторые
силы, одна из которых
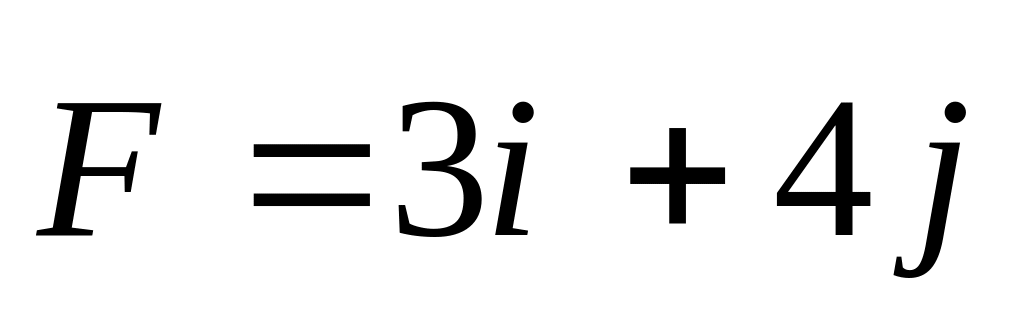 .
Найти работу, которую совершила сила
F. Здесь r1,
r2
и F — в СИ.
.
Найти работу, которую совершила сила
F. Здесь r1,
r2
и F — в СИ.Н
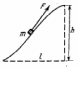 ебольшое
тело массы
медленно втащили на горку, действуя
силой
ебольшое
тело массы
медленно втащили на горку, действуя
силой
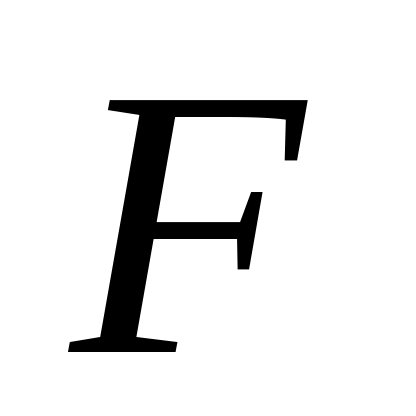 ,
которая в каждой точке направлена по
касательной к траектории (см. рисунок).
Найти работу этой силы, если высота
горки
,
длина основания
и коэффициент трения
,
которая в каждой точке направлена по
касательной к траектории (см. рисунок).
Найти работу этой силы, если высота
горки
,
длина основания
и коэффициент трения
 .
.
Решение:
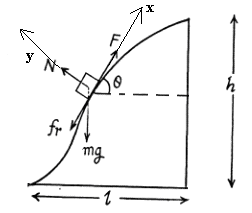 Работа
– скалярное произведение вектора силы
на вектор перемещения тела.
Работа
– скалярное произведение вектора силы
на вектор перемещения тела.
![]() ,
(1)
,
(1)
так
как направление силы
![]() совпадает с направлением вектора
перемещения
совпадает с направлением вектора
перемещения
![]() и
и
![]() .
.
Уравнение движения для тела
![]() (2)
(2)
Введем систему координат как указано на рисунке. Запишем проекции уравнения (2) на оси координат.
Ox:
![]() (3)
(3)
Oy:
![]() (4)
(4)
Из
(4)
![]() и
и
![]() - сила трения.
- сила трения.
Подставим
значение для силы трения в (3) и получим
для
![]()
![]() (5)
(5)
Тогда работа будет равна
![]()
Ответ:
![]() .
.
Тело массы m начинают поднимать с поверхности Земли, приложив к нему силу F, которую изменяют с высотой подъема у по закону
 ,
где а - положительная постоянная. Найти
работу этой силы и приращение потенциальной
энергии тела в поле тяжести Земли на
первой половине пути подъема.
,
где а - положительная постоянная. Найти
работу этой силы и приращение потенциальной
энергии тела в поле тяжести Земли на
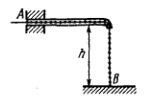
первой половине пути подъема.Н
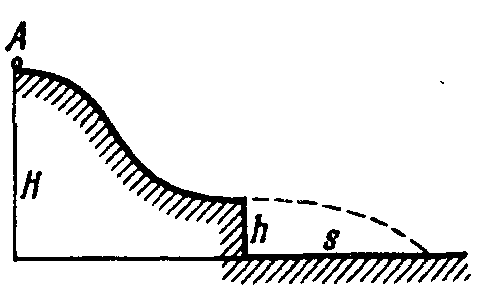 ебольшая
шайба А соскальзывает без начальной
скорости с вершины гладкой горки высотой
H,
имеющей горизонтальный трамплин (см.
рисунок). При какой высоте h трамплина
шайба пролетит наибольшее расстояние
s ? Чему оно равно?
ебольшая
шайба А соскальзывает без начальной
скорости с вершины гладкой горки высотой
H,
имеющей горизонтальный трамплин (см.
рисунок). При какой высоте h трамплина
шайба пролетит наибольшее расстояние
s ? Чему оно равно?
Домашняя работа: №№ 1.147, 1.144, 1.149, 1.174, 1.196. Иродов И.Е. Задачи по общей физики. М.: Бином. Лаб. знаний, 2007
Практическое занятие № 10 Силовое поле. Связь силы с потенциальной энергией – 2 часа
Закрепление теоретических сведений, результатов лабораторных практикумов и навыков расчета величин в рамках темы «Динамика»
Содержание задания:
Предварительная подготовка к рассмотрению темы, заключающая в составление и записи студентами под руководством преподавателя краткого конспекта формул, необходимых для решения задач, которые известны из ранее прошедшего лекционного занятия;
рассмотрение примеров физических явлений, изучаемых в данной теме, приводимых студентами, которые известны из повседневного была, личного опыта, промышленного использования или лабораторных работ.
Решение и обсуждение студентами (индивидуально или триадами) под руководством преподавателя следующих задач:
Частица движется вдоль оси х под действием силы поля
 ,
где α=8,0Н/м, β=6,0Н/м2.
Найти координату x0
точки, в которой потенциальная энергия
частицы такая же, как в точке x=0.
,
где α=8,0Н/м, β=6,0Н/м2.
Найти координату x0
точки, в которой потенциальная энергия
частицы такая же, как в точке x=0.
Потенциальная энергия частицы в некотором поле имеет вид
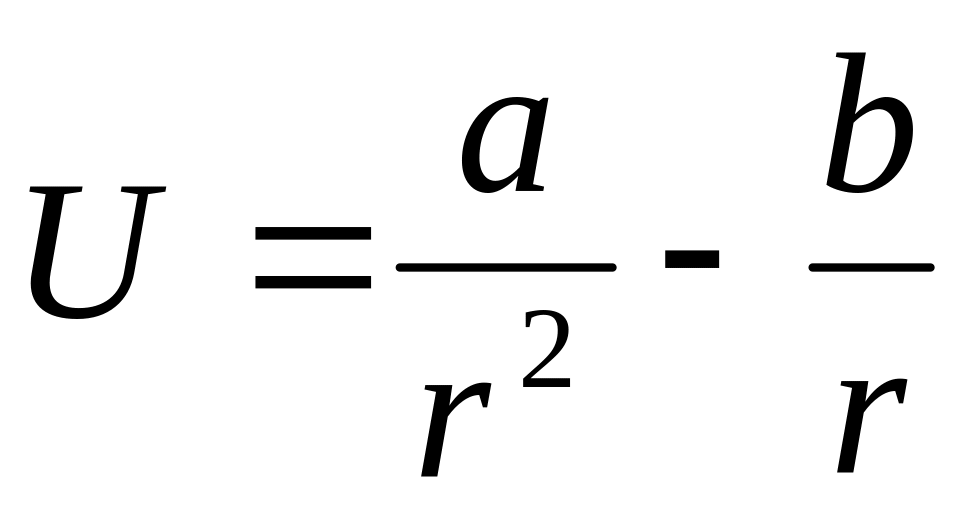 ,
где а и b — положительные постоянные,
r
— расстояние от центра поля. Найти:
а) значение r0,
соответствующее равновесному положению
частицы; выяснить, устойчиво ли это
положение; б) максимальное значение
силы притяжения; изобразить примерные
графики зависимостей U(r) и Fr(r).
,
где а и b — положительные постоянные,
r
— расстояние от центра поля. Найти:
а) значение r0,
соответствующее равновесному положению
частицы; выяснить, устойчиво ли это
положение; б) максимальное значение
силы притяжения; изобразить примерные
графики зависимостей U(r) и Fr(r).Частица массы m=4,0г движется в двумерном поле, где ее потенциальная энергия
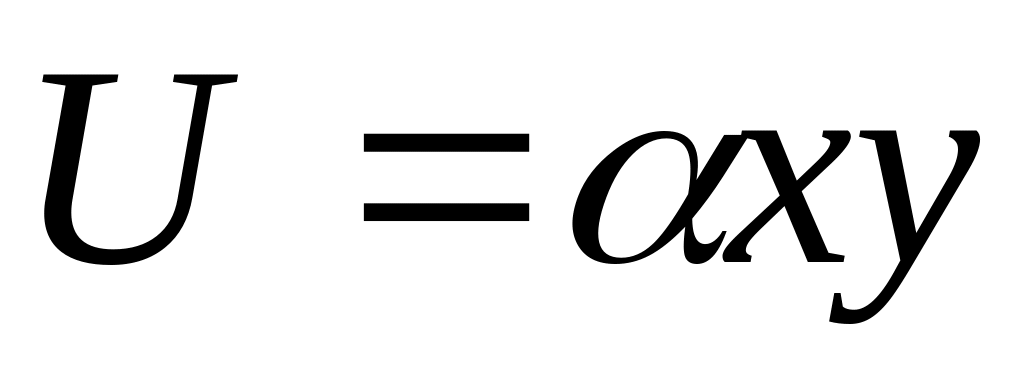 и
=0,19
мДж/м2.
В точке 1 {3,0м, 4,0м} частица имела скорость
и
=0,19
мДж/м2.
В точке 1 {3,0м, 4,0м} частица имела скорость
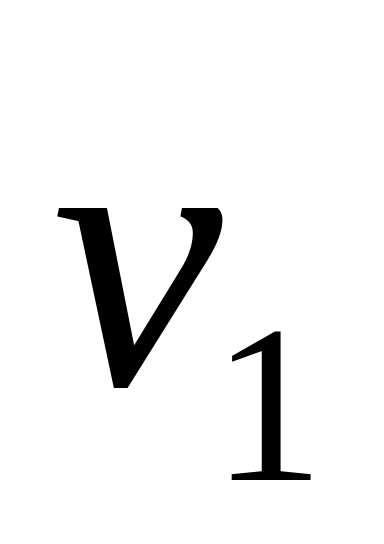 =3,0м/с,
а в точке 2 {5,0 м, -6,0 м} скорость
=3,0м/с,
а в точке 2 {5,0 м, -6,0 м} скорость
 =4,0м/с.
Найти работу сторонних сил на пути
между точками 1 и 2.
=4,0м/с.
Найти работу сторонних сил на пути
между точками 1 и 2.
Домашняя работа: №№ 1.168, 1.172, 1.191, 1.194. Иродов И.Е. Задачи по общей физики. М.: Бином. Лаб. знаний, 2007
Практическое занятие № 11 «Законы сохранения импульса, момента импульса и энергии»
Закрепление теоретических сведений, результатов лабораторных практикумов и навыков расчета величин в рамках темы «Динамика»
Содержание задания:
Предварительная подготовка к рассмотрению темы, заключающая в составление и записи студентами под руководством преподавателя краткого конспекта формул, необходимых для решения задач, которые известны из ранее прошедшего лекционного занятия;
рассмотрение примеров физических явлений, изучаемых в данной теме, приводимых студентами, которые известны из повседневного была, личного опыта, промышленного использования или лабораторных работ.
Решение и обсуждение студентами (индивидуально или триадами) под руководством преподавателя следующих задач:
Н
 а
гладкой горизонтальной плоскости
движется небольшое тело массы
а
гладкой горизонтальной плоскости
движется небольшое тело массы
 ,
привязанное к нерастяжимой нити, другой
конец которой втягивают в отверстие
,
привязанное к нерастяжимой нити, другой
конец которой втягивают в отверстие
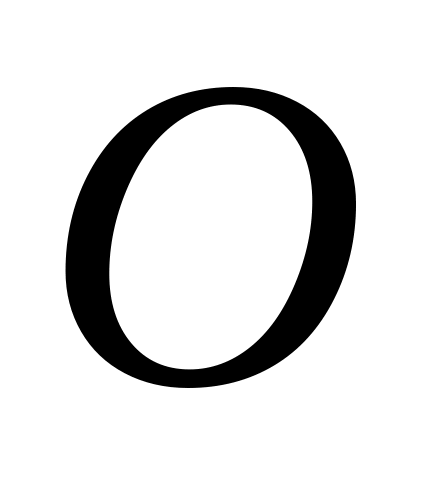 (см. рис.) с постоянной скоростью. Найти
силу натяжения нити в зависимости от
расстояния
(см. рис.) с постоянной скоростью. Найти
силу натяжения нити в зависимости от
расстояния
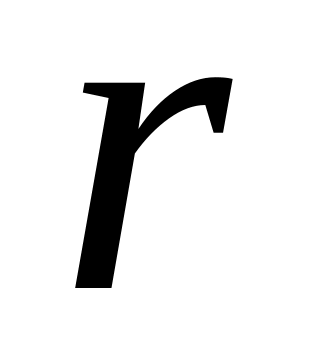 тела до отверстия, если при
тела до отверстия, если при
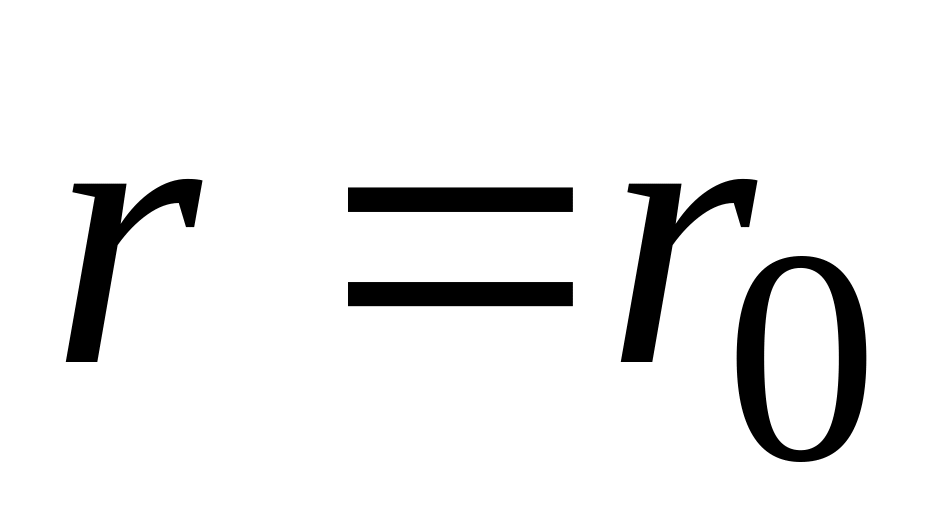 угловая скорость нити была равна
угловая скорость нити была равна
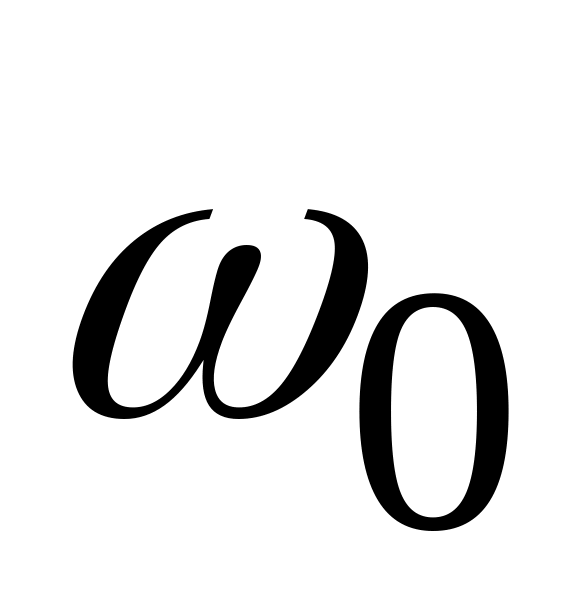 .
.
Р ешение:
ешение:
Используя закон сохранения момента импульса:
![]() (1)
и зная, что
(1)
и зная, что
![]() (скорость направлена по касательной к
траектории), запишем:
(скорость направлена по касательной к
траектории), запишем:
![]() (
(![]() )
)
![]() ,
т.к.
,
т.к.
![]()
![]() (2),
сокращаем правое и левое выражения на
.
(2),
сокращаем правое и левое выражения на
.
![]() (3).
(3).
На
тело действует центростремительная
сила
![]() (4). Зная что
(4). Зная что
![]() ,
сила равна
,
сила равна
![]() .
Подставим в (4) выражение для угловой
скорости (3)
.
Подставим в (4) выражение для угловой
скорости (3)
![]() .
.
Ответ:
![]() .
.
Небольшое тело движется по замкнутой траектории в центральном силовом поле, где его потенциальная энергия пропорциональна квадрату расстояния до центра поля. Наименьшее расстояние тела до центра поля равно r0, a наибольшее - в η раз больше. Найти радиус кривизны траектории тела в точке, соответствующей r0.
Замкнутая система состоит из двух частиц с массами m1 и m2, движущихся под прямым углом друг к другу со скоростями v1 и v2. Найти в системе их центра масс: а) импульс каждой частицы; б) суммарную кинетическую энергию обеих частиц.
Домашняя работа: №№ 1.224, 1.213, 1.206. Иродов И.Е. Задачи по общей физики. М.: Бином. Лаб. знаний, 2007
Практическое занятие № 12 «Упругие и неупругие столкновения. Законы сохранения при столкновениях»
Закрепление теоретических сведений, результатов лабораторных практикумов и навыков расчета величин в рамках темы «Динамика».
