13.4.4. Методы линеаризации

Идея методов заключается в сведении задачи нелинейного программирования к задаче линейного программирования. С этой целью нелинейные функции целевой функции W(x) и ограничений g(x), h(x) в ряд Тейлора до членов первого порядка в окрестности точки линеаризации x^t, что позволяет W(x), g(x), h(x) аппроксимировать линейными функциями и свести общую задачу нелинейного программирования

к следующей задаче линейного программирования

Решая ее при помощи методов линейного программирования, находим новое приближение x^t+1. В случае нелинейных функций точка x^t+1 -обычно недопустимая точка. Однако для сходимости к оптимуму достаточно, чтобы последовательность точек {x^t}, полученных в результате решения последовательности подзадач линейного программирования, выполнялось следующее условие: значение целевой функции W и невязки по ограничениям в x^t+1 должно быть меньше их значений в точке x^t.

13.5. Решение задач нелинейной оптимизации на эвм

Ряд программных продуктов позволяют решать задачи оптимизационные задачи в нелинейной постановке, например пакеты LINGO и MS Excel. Для последнего последовательность действий аналогична решению задачи линейной оптимизации (см. п. 9.7). В качестве примера на рис. 13.9 - 13.11 продемонстрировано решение задачи условной нелинейной оптимизации примера 13.9 в целочисленной постановке.

Рис. 13.9.

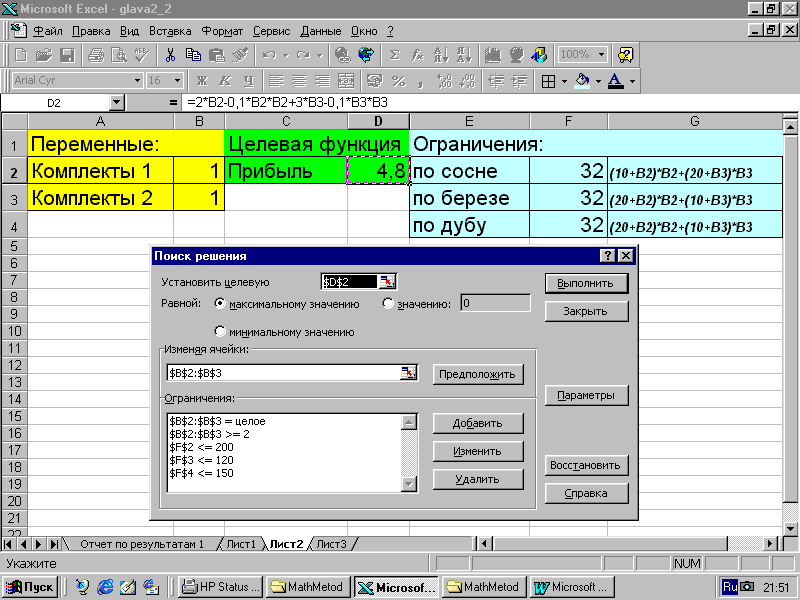
Рис. 13.10.

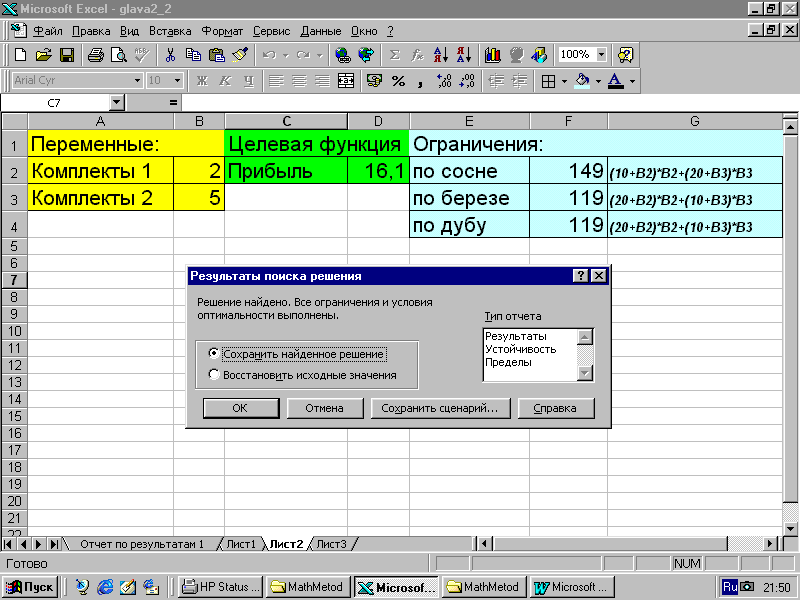
Рис. 13.11.

13.6. Контрольные вопросы и задания

1. Приведите математическую формулировку основной задачи безусловной однопараметрической оптимизации.

2. В чем состоит свойство унимодальности функций и в чем заключается важное значение этого свойства при решении задач одномерной оптимизации?

3. Сформулируйте условие, при выполнении которого метод полиномиальной аппроксимации может не привести к получению правильного решения.

4. При реализации поисковых методов рекомендуется принимать решение об окончании поиска на основе проверок как величины разности значений переменной, так и величины разности значений целевых функций. Возможна ли ситуация, когда результат одной из проверок, указывает на сходимость к точке минимума, тогда как полученная точка в действительности минимуму не соответствует? Поясните ответ рисунком.

5. Бревно длиной в 20 м имеет форму конуса, диаметры оснований которого равны соответственно 0,3 и 0,2 м. Требуется автоматизировать процесс раскроя бревна для получения бруса квадратного поперечного сечения, ось которого совпадала бы с осью бревна и объем которого был бы наибольшим. Каковы должны быть размеры бруса? Принять = 0,01.

6. Требуется автоматизировать процесс раскроя листа металла размером 2 х 1,5 м, из углов которого необходимо вырезать одинаковые квадраты так, чтобы, согнув лист, получить коробку наибольшей вместительности. Какова должна быть сторона вырезаемого квадрата? Принять = 0,01.

7. Приведите математическую формулировку основной задачи безусловной многопараметрической оптимизации.

8. Опишите две ситуации, в которых метод поиска по симплексу оказывается более предпочтительным, чем метод сопряженных направлений Пауэлла.

9. Почему квадратичные функции используются как основа для построения алгоритмов нелинейной оптимизации?

10. Определить место строительства предприятия между двумя пунктами сбыта, расстояние между которыми 200 км, и размер поставок в каждый из пунктов, если выпуск продукции завода составляет 150 единиц. Зависимость продажной цены единицы продукции в каждом из пунктов сбыта от объема поставок V_i и затрат на перевозку единицы продукции от расстояния S_i (в км) между предприятием и пунктом сбыта заданы в табл. 13.4.

Таблица 13.4.

Вариант	Метод поиска	Пункт сбыта	Продажная цена, руб	Затраты на перевозку, руб
1	Поиск по симплексу	1 2	450-1,0*V1 420-0,8*V2	15+0,1*S1 15+0,05*S2
2	Хука-Дживса	1 2	380-1,3*V1 330-0,7*V2	18+0,1*S1 18+0,08*S2
3	Пауэлла	1 2	230-0,9*V1 210-0,6*V2	19+0,08*S1 19+0,04*S2

11. Найти оптимальный план выпуска двух видов продукции с учетом ограниченных ресурсов сырья (120 кг), электроэнергии (280 квтч) и оборудования (300 машино-часов) при следующих нормах расхода на единицу продукции: сырья 3 и 2 кг, электроэнергии 4 и 7 квтч и оборудования 50-5х₁ и 20-4х₂, где х₁ и х₂ - искомое число производимых единиц 1 и 2 вида.

12. Предприятие выпускает изделия А и Б, при изготовлении которых расходуется сырье вида 1 и 2. Известны запасы, нормы его расхода, оптовые цены на изделия и их себестоимость. Как только объем выпускаемой продукции перестает соответствовать оптимальным размерам предприятия, дальнейшее увеличение выпуска ведет к повышению себестоимости продукции, и в этих условиях фактическая себестоимость в первом приближении описывается линейной функцией c = c⁰ +c^’ x, где с^’ - постоянная величина, х - объем выпускаемой продукции. Оптимизировать план выпуска продукции по данным табл. 13.5.

Таблица 13.5

Вариант	a10	a10	a10	a10	a10	a10	p1	p2	c10	c20	c1’	c2’
1	90	88	3	6	8	11	12	10	7	8	0,2	0,2
2	30	60	5	2	8	11	8	7	6	4	0,1	0,1
3	60	10	11	8	1	2	10	11	7	9	0,1	0,1
4	14	42	1	4	7	3	15	13	14	11	0,2	0,2
5	7	10	1	1	1	2	12	11	9	10	0,2	0,2
6	51	99	5	13	15	7	15	13	13	10	0,1	0,1
7	40	84	4	7	12	11	17	9	14	15	0,2	0,2
8	13	10	2	3	2	1	14	16	12	13	0,2	0,2
9	72	10	9	8	1	2	23	19	20	13	0,3	0,3
10	84	31	7	12	5	3	21	27	15	24	0,3	0,3

13. Из теоретических соображений известно, что связь между зависимой переменной y и переменной x можно описать двухпараметрической функцией y(x)=(a*x)/(1+b*x). Значения параметров a и b определяются в соответствии с критерием наименьших квадратов на основе экспериментальных данных, представленных в табл. 13.6. Найти a и b.

Таблица 13.6

Вариант	Метод	y	1,0	2,0	3,0	4,0
1	Симплекс	x	1,05	1,25	1,55	1,59
2	Хука-Дживса	x	1,04	1,27	1,51	1,56
3	Пауэлла	x	1,01	1,21	1,49	1,55

14. Требуется переправить V м³ опилок деревообрабатывающего предприятия на целлюлозно-бумажный комбинат. Для перевозки груза необходимо сконструировать герметичный контейнер таким образом, чтобы минимизировать полные затраты на перевозку груза. Известны следующие данные (табл. 13.7): стоимость каждого рейса p, руб; удельная стоимость материала днища a, руб/м², боковых стенок b, руб/м²; крышки с, руб/м²; стоимость погонного метра сварного шва d руб.

Таблица 13.7.

Вари-ант	Метод	V	p	a	b	c	d
1	Симплекс	400	250	45	21,2	5,4	1,5
2	Хука-Дживса	600	360	40	20,8	10,6	3,5
3	Пауэлла	900	670	35	19,5	7,4	2,7

ЗАКЛЮЧЕНИЕ

Ввиду ограниченного объема учебной дисциплины по разделу ”Математические методы и модели в расчетах на ЭВМ” некоторые вопросы не вошли в учебное издание. В частности, не отражены методы многокритериальной оптимизации, которые позволяют находить оптимальное решение не только по экономическим, лесоводственным, технологическим критериям, но и учитывать экологические, природноохранные и социальные аспекты. Недостаточно полно представлены модели имитационного моделирования, которые позволяют выбирать наиболее рациональные решения путем предварительного имитирования производственных ситуаций на ЭВМ. Много и других методов исследования операций, например, марковских процессов принятия решеий, теории игр успешно применяются или могут быть использованы в лесном деле и науке для принятия оптимальных решений в условиях дефицита информации и риска. Тем не менее, опираясь на знание материала данного учебника, можно самостоятельно освоить новые методы и грамотно их применять в своей практической работе.

Рассмотренные примеры оптимизационных моделей достаточно просты и порой недостаточно адекватно отражают реальные производственные процессы. Тем не менее разработка более сложных и точных моделей базируется на изложенном в учебнике системном подходе, алгоритмах математического моделирования и оптимизации, но требует более глубокого и детального исследования производственной ситуации, что определяется уже профессиональной подготовкой специалиста.