13.2.2. Методы полиномиальной аппроксимации

Сущность метода. Согласно теореме Вейерштрасса об аппроксимации, непрерывную функцию в некотором интервале можно аппроксимировать полиномом достаточно высокого порядка. Следовательно, если функция унимодальна и найден полином, который достаточно точно ее аппроксимирует, то координаты точки оптимума функции можно оценить путем вычисления координаты точки оптимума полинома.

Квадратичная аппроксимация

Простейший случай основан на том факте, что функция, принимающая минимальное значение во внутренней точке интервала, должна быть по крайней мере квадратичной.

Если целевая функция W(x) в точках x₁, x₂, x₃ принимает соответствующие значения W₁, W₂, W₃, то можно определить коэффициенты a_о, a₁, a₂ таким образом, что значения квадратичной функции

q(x) = a_o + a₁(x-x₁) + a₂(x-x₁)(x-x₂)

совпадут со значением W(x) в трех указанных точках. Вычислим q(x) в трех указанных точках.

W1 = W(x1) = q(x1) = ao	 ao = W1
W2 = W(x2) = q(x2) = W1 + a1(x2 - x1)	 a1 =(W2 - W1)/(x2 - x1)
W3 =q(x3) = W1 + [(W2 - W1) (x3 - x1)]/ /(x2 - x1) + a2(x3 - x1) (x3 - x2)	 a2 =
	

Метод Пауэлла

Шаг 1. x₂ = x₁ + x.

Шаг 2. Вычислить W(x₁) и W(x₂).

Шаг 3.

• Если W(x₁) > W(x₂), то x₃ = x₁ + 2 x.

• Если W(x₁)  W(x₂), то x₃ = x₁ - x.

W(x₁) > W(x₂),

Шаг 4. Вычислить W(x₃) и найти

Wmin = min{ W(x₁),W(x₂), W(x₃)},

Xmin = x_i, соответствующая Wmin.

Шаг 5. По x₁, x₂, x₃ вычислить x^*, используя формулу для оценивания с помощью квадратической аппроксимации.

Шаг 6. Проверка окончания

1. Если Wmin - W(x^*) < _W, то закончить поиск. В противном случае к шагу 7.

2. Если Xmin - x^* < _x, то закончить поиск. В противном случае к шагу 7.

Шаг 7. Выбрать Xmin или x^* и две точки по обе стороны от нее. Обозначить в естественном порядке и перейти к шагу 4.

13.2.3. Методы с использованием производных

Целесообразно предположить, что эффективность поисковых процедур существенно повысится, если в дополнение к условию непрерывности ввести требование дифференцируемости целевой функции. Необходимое условие существования оптимума целевой функции в точке x^*

W’(x^*) = dW/dx _x=x* = 0. (13.2)

В том случае, если целевая функция содержит члены, включающие x в третьей и более высоких степенях, то получение аналитического решения уравнения W’(x) затруднительно. В этих случаях целесообразно использовать численные методы нахождения корней нелинейных уравнений:

• метод хорд;

• метод касательных;

• метод средней точки.

Метод средней точки

Сущность метода. Основан на алгоритме исключения интервалов, на каждой итерации которого рассматривается одна пробная точка R. Если в точке R выполняется неравенство W’(R) < 0, то вследствие унимодальности функции точка оптимума не может лежать левее точки R. Аналогично, если W’(R) > 0, то интервал x>R можно исключить.

Пусть в интервале [a,b] имеются две точки N и P, в которых производные W’(N)<0 и W’(P)>0. Оптимальная точка x^* расположена между N и P.

Шаг 1. Положить P=b, N=a, причем W’(a)<0 и W’(b)>0.

Шаг 2. Вычислить R=(P+N)/2 и W’(R).

Шаг 3. Если W’(R) < , то закончить поиск. В противном случае, если W’(R)<0, положить N=R, и перейти к шагу 2. Если W’(R) > , положить P=R и перейти к шагу 2.

Как следует из логической структуры, процедура поиска по методу средней точки основана на исследовании только знака производной.

Пример 13.5. Приложение метода средней точки к задаче оптимального раскроя бревна на брус.

W(l)=(l/2)(d_k -(d_k-d_o)l/l_o)²  max,

где

l_o=0,10,

d_k =0,22,

d_o =0,12

в интервале 5l9 (см. пример 3.3) при =0,0001.

W’(l) = dW(l)/dl = 0,0242 – 0,0044 l + 0,00015 l².

Итерация 1.

Шаг 1. W’(5)=0,00595, W’(9) = -0,00325, N=9, P=5.

Шаг 2. R=(9+5)/2=7.

Шаг 3. W’(7)=0,00075>0; W’(7)  0,0001, положить P=7.

Итерация 2.

Шаг 2. R=(9+7)/2=8.

Шаг 3. W’(8)=-0,00140; W’(7)  0,0001, положить N=8.

Итерация 3.

Шаг 2. R=(8+7)/2=7,5.

Шаг 3. W’(7,5)=-0,000360; W’(7,5)  0,0001, положить N=7,5.

Итерация 4.

Шаг 2. R=(7,5+7)/2=7,25.

Шаг 3. W’(7,25)=0,000184>0; W’(7,25)  0,0001, положить Р=7,25.

Итерация 5.

Шаг 2. R=(7,25+7,5)/2=7,375.

Шаг 3. W’(7,375)= -0,000091<0; W’(7,375)  0,0001, решение l^*=7,375 при котором W^*(7,375)= 0,0789 найдено с заданной точностью.

Метод хорд

Сущность метода. Ориентирован на нахождение корня уравнения W’(x) в интервале [a,b], в котором имеются две точки N и P, в которых знаки производных различны. Алгоритм метода хорд позволяет аппроксимировать функцию W’(x) “хордой” и найти точку, в которой секущая графика W’(x) пересекает ось абсцисс (рис. 13.1).

Шаг 1. Следующее приближение к стационарной точке x^* определяется по формуле

R = P - . (13.3)

Шаг 2. Вычислить W’(R).

Шаг 3. Если W’(R) < , то закончить поиск. В противном случае необходимо выбрать одну из точек P или N, чтобы знаки производных в этой точке и точке R были различны. Вернуться к шагу 1.

Как видно из алгоритма, метод хорд реализован на исследовании как знака производной, так и ее значении. Поэтому он более эффективен, чем метод средней точки.

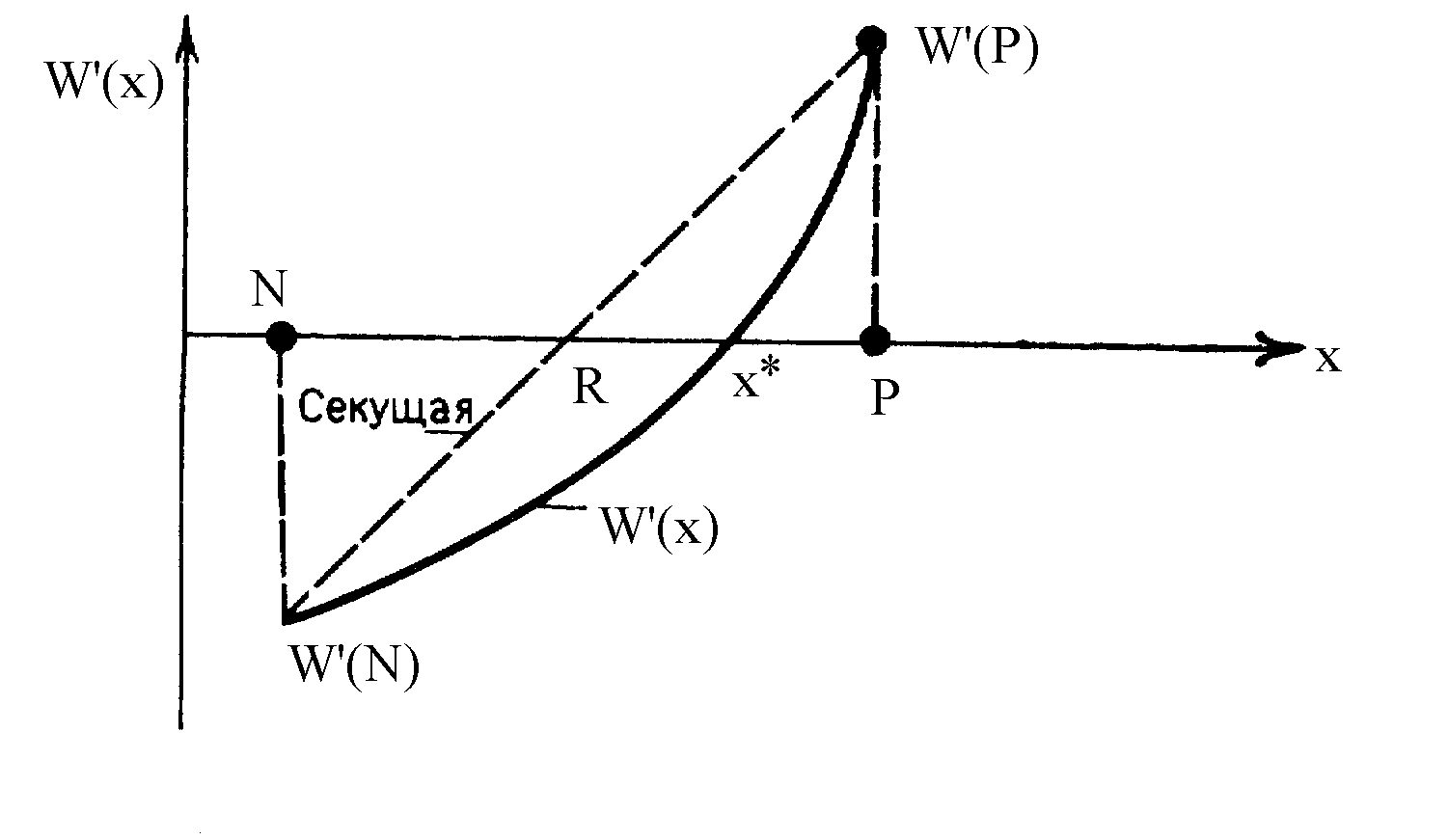
Рис. 13..3. Схема метода хорд

Пример 13.6. Приложение метода хорд к задаче оптимального раскроя бревна на брус.

W(l)=(l/2)(d_k -(d_k-d_o)l/l_o)²  max,

где

l_o=0,10,

d_k =0,22,

d_o =0,12

в интервале 5l9 (см. пример 3.3) при =0,0001.

W’(l) = dW(l)/dl = 0,0242 – 0,0044 l + 0,00015 l².

Итерация 1.

Шаг 1. W’(5)=0,00595, W’(9) = -0,00325, N=9, P=5.

Шаг 2. R=5-{(0,00595*(5-9))/(0,00595+0,00325)}=7,587.

Шаг 3. W’(7,587)= -0,00055<0; W’(7,587)  0,0001, положить N=7,587.

Итерация 2.

Шаг 2. R=5-{(0,00595*(5-7,587))/(0,00595+0,00055)}=7,368.

Шаг 3. W’(7,368)= -0,000076<0; W’(7,368)  0,0001, решение l^*=7,368, при котором W^*(7,368)= 0,0789, найдено с заданной точностью.

Метод касательных

Сущность метода. Ориентирован на нахождение корня уравнения W’(x) в интервале [a,b], в котором имеются две точки N и P, в которых знаки производных различны (рис.13.4). Работа алгоритма начинается из точки x_o, которая представляет начальное приближение корня уравнения W’(x)=0. Далее строится линейная аппроксимация функции W’(x) в точке x₁, и точка, в которой аппроксимирующая линейная функция обращается в нуль, принимается в качестве следующего приближения. Если точка x_k принята в качестве текущего приближения к оптимальной точке, то линейная функция, аппроксимирующая функцию W’(x) в точке x_k, записывается в виде

W’(x,x_k) = W’(x_k) + W’’(x_k)(x-x_k). (13.4)

Приравняв правую часть уравнения к нулю, получим следующее приближение к искомой точке:

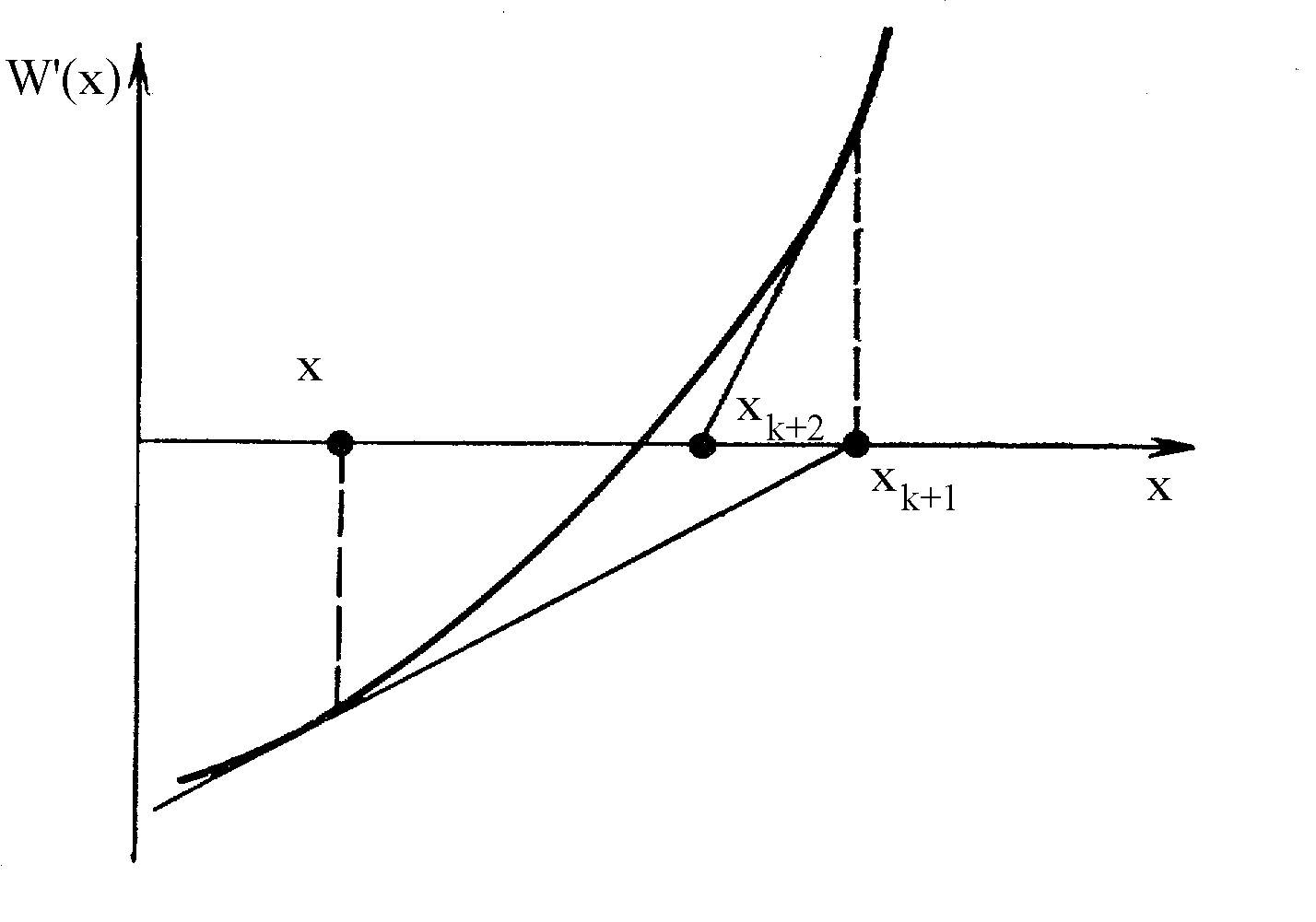
Рис. 13.4. Схема метода касательных

Шаг 1. Следующее приближение к стационарной точке x^* определяется по формуле:

x_k+1 = x_k - [W’(x_k)/W’’(x_k)].

Шаг 2. Вычислить W’(x_k+1), W’’(x_k+1)

Шаг 3. Если W’(x_k+1) < , то закончить поиск. В противном случае необходимо вернуться к шагу 1.

Как явствует из алгоритма, целевая функция W(x) должна быть

дважды дифференцируема.

Пример 13.7. Приложение метода касательных к задаче оптимального раскроя бревна на брус.

W(l)=(l/2)(d_k -(d_k-d_o)l/l_o)²  max,

где

l_o=0,10,

d_k =0,22,

d_o =0,12

в интервале 5l9 (см. пример 3.3) при =0,0001.

W’(l) = dW(l)/dl = 0,0242 – 0,0044 l + 0,00015 l².

W’’(l) = dW’(l)/dl = – 0,0044 + 0,0003 l.

Итерация 1.

Шаг 1. l₁=5; W’(5)=0,00595, W’’(5) = -0,0029, l₂=5-(0,00595/-0,0029)=7,052;

Шаг 2. W’(7,052)= 0,000631 0,0001.

Итерация 2.

Шаг 1. l₁=7,052; W’(7,052)= 0,000631, W’’(7,052) = -0,00228,

l₃=7,052-(0,000631/-0,00228)=7,329;

Шаг 2. W’(7,329)= 0,00000954 0,0001, решение l^*=7,329, при котором W^*(7,329)= 0,0789, найдено с заданной точностью.