2.3. Графическое представление вариационных рядов

После того как произведена группировка совокупности по разрядам, характер распределения более или менее проясняется. Однако более наглядное представление этого распределения дает графическое изображение. Среди многих способов графического изображения распределений чаще всего применяются два способа: построение полигона (т.е. многоугольника) частот и построение гистограммы (столбчатой диаграммы).

П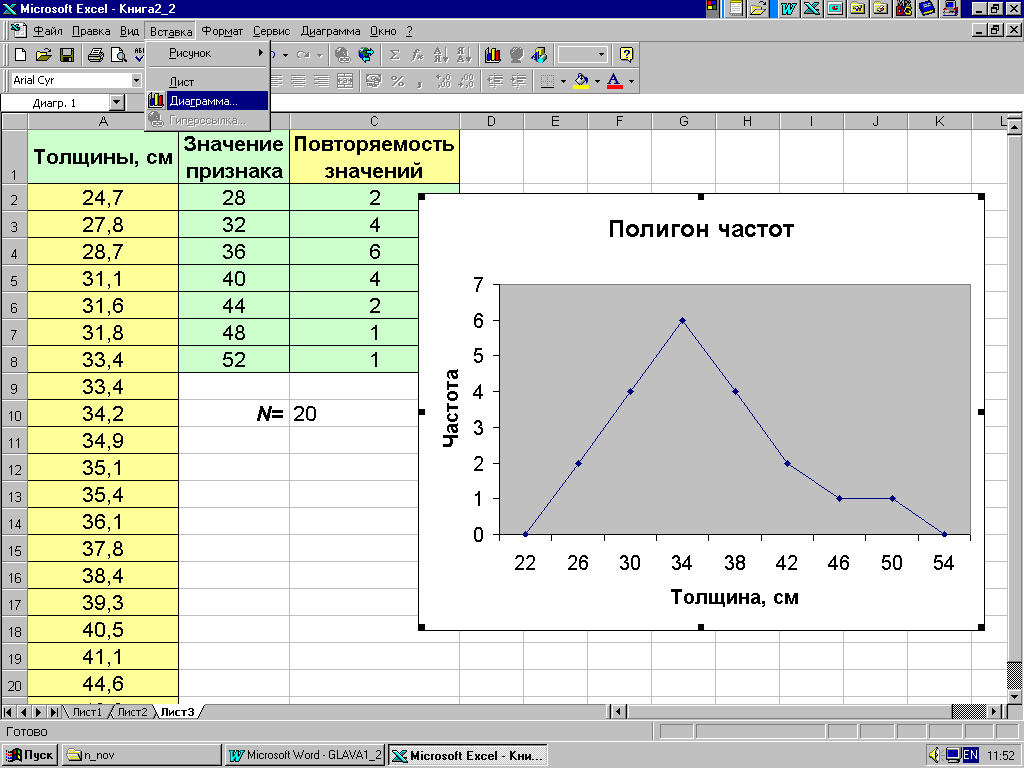 ри построении полигона все значении, лежащие в данном разряде (ступени толщины), "стягиваются" к середине этого разряда. Например, в ступень 28-32 см (рис. 2.4) попадает 4 ствола, которые, вообще говоря, имеют разную толщину (28,7; 31,1; 31,6; 31,8); между тем мы условно считаем, что все 4 ствола имеют толщину 30 cм, соответствующую середине разряда. То же относится и к остальным разрядам. После этого строится график так, как это показано на рис. 2.4. Точки, соответствующие каждому из разрядов, отстоят от горизонтальной оси (оси абсцисс) на расстояния, пропорциональные соответствующим частотам. Разумеется, масштабы могут быть по обеим осям произвольные, но зачастую рекомендуется выбирать их так, чтобы соотношение ширины и высоты графика было близко к 1 : 2.

Р

24 28 32 36 40 44 48 52 56

ис. 2.4.

На рис. 2.4 представлен полигон частот распределения, приведенный в примере 2.1. От крайних разрядов отложено в обе стороны еще по одному разряду с нулевыми частотами для придания полигону частот завершенного вида. Для построения диаграммы использована процедура "Диаграмма" меню "Вставка".

На гистограмме каждый разряд изображается прямоугольником с шириной, пропорциональной ширине разряда, и с высотой, пропорциональной частоте данного разряда. Для распределения, приведенного в примере 2.1, получается картина, представленная с помощью MS Excel на рис. 2.5.

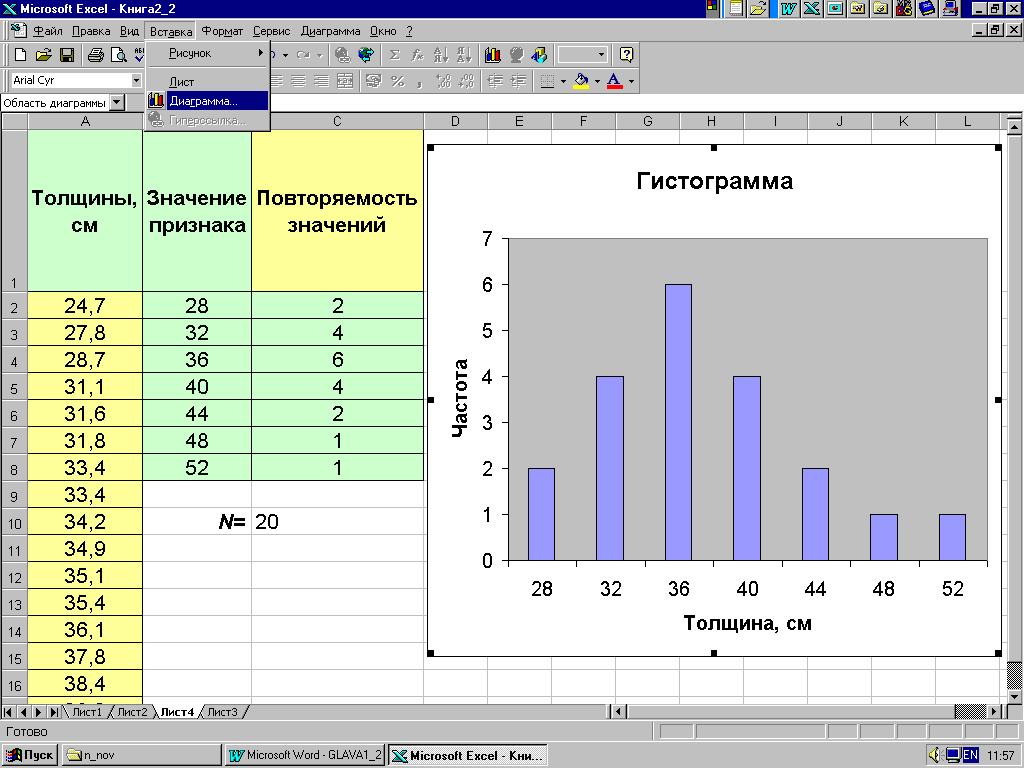
Рис. 2.5.

Изображение распределения при помощи гистограммы представляет собой другой крайний случай идеализации: если в случае полигона частот все значения, лежащие внутри разряда, «стягиваются» к середине разряда, то в случае гистограммы они считаются распределенными равномерно по всему разряду. Поэтому в принципиальном отношении оба способа изображения следует считать равноценными, и выбор между ними определяется чаще всего привычкой или вкусом исследователя. Впрочем, иногда отмечают, как преимущество, что площадь, ограниченная гистограммой, пропорциональна объему совокупности, в то время как площадь, ограниченная полигоном частот и осью абсцисс, не имеет такой простой интерпретации. С другой стороны, если совокупность дискретна, то естественно ее следует изображать полигоном частот.

При порядковых градациях графическое изображение излишне, так как в принципе каждому рангу отвечает одна варианта; случаи совпадающих рангов, о которых упоминалось выше, составляют ту характерную особенность совокупности, которую следует специально выделять.

Зачастую вариационный ряд графически представляют в виде кривой накопленного распределения частот, называемой кумулятой или огивой. Для ее построения на оси абсцисс откладываются значения дискретного признака (или границы разряда), а на оси ординат - нарастающие итоги частот, соответствующие этим значениям признака (или верхним границам разрядов). Кумулята распределения девевьев по толщине приведена на рис. 2.6.

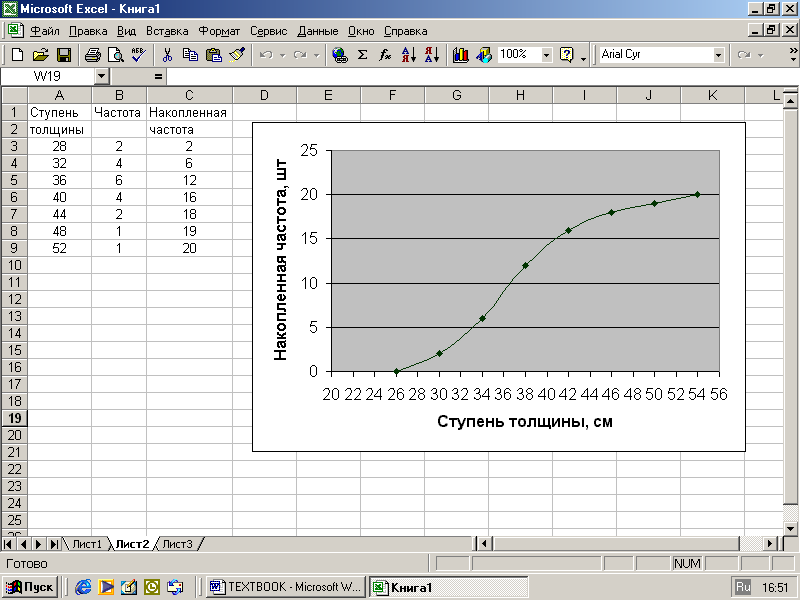
Рис. 2.6

При качественной классификации употребляется, как правило, изображение с помощью гистограммы. На рис. 2.7 показана гистограмма для совокупности, объединяющая данные по разным видам пилопродукции (доход, тыс.руб). Важно подчеркнуть, что, в отличие от количественной и порядковой группировки, при качественной классификации можно произвольно переставлять местами разряды группировки, располагая их в любом порядке (в данном случае они расположены просто по алфавиту). Поэтому здесь точная форма гистограммы не имеет никакого значения. Иногда оказывается удобным расположить разряды по убывающим или возрастающим частотам, если нет особых оснований для какого-либо другого расположения.

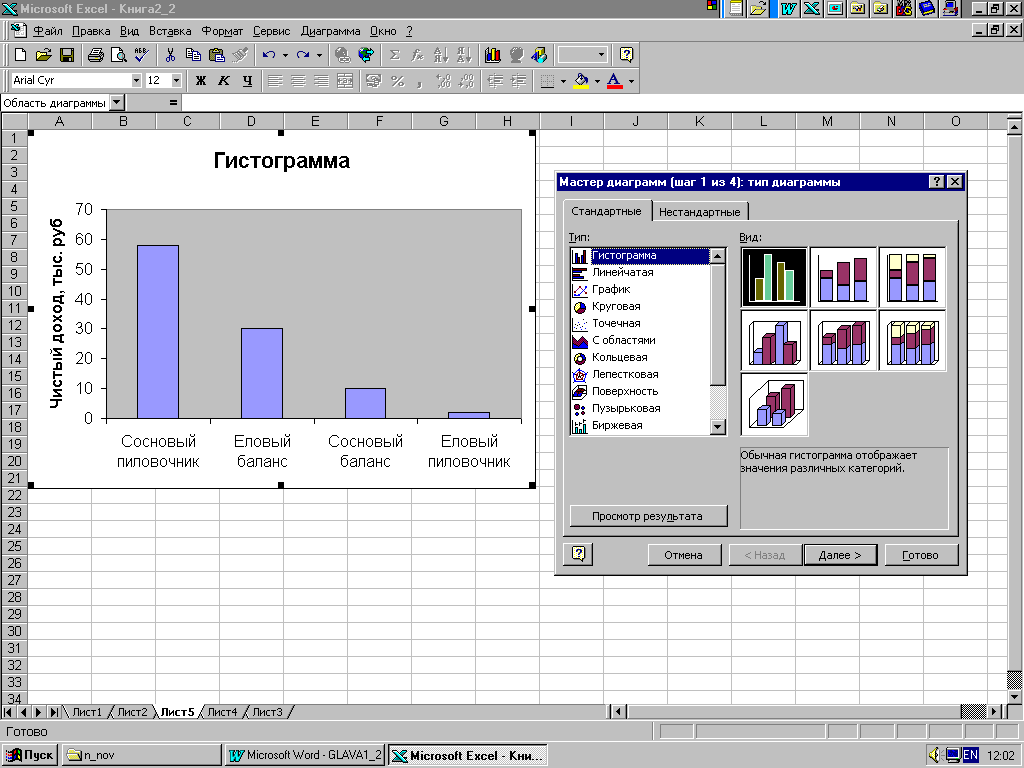
Рис. 2.7.

2.4. Статистические показатели эмпирических совокупностей

Одной из основных задач статистической обработки наблюдений является нахождение небольшого набора показателей, представляющих в обобщенном виде свойства полученной статистической совокупности.

Существенной характеристикой статистической совокупности является объем выборки N. Изменение N при неизменном характере ее статистического распределения означает пропорциональное увеличение или уменьшение всех частот. Геометрически это соответствует растяжению или сжатию графика по вертикали.

Статистические характеристики эмпирических совокупностей принято подразделять на показатели:

• центрирующей тенденции;

• вариации;

• скошенности и крутизны.