9.5. Метод искусственных переменных

Для получения системы в каноническом виде, обладающей допустимым базисным решением, существует специальный метод. Сначала задача ЛП приводится к стандартной форме, в которой все переменные неотрицательные. Затем для каждого ограничения проверяется существование соответствующей базисной переменной. Если ее нет, то вводится новая искусственная переменная, играющая роль базисной для данного ограничения. После проверки всех ограничений получается система в каноническом виде и появляется возможность заполнить начальную симплексную таблицу. Так как введенные переменные не имеют отношения к существу задачи ЛП в исходной постановке, то необходимо добиться обращения в нуль искусственных переменных. Этого можно сделать с помощью двухэтапного симплекс-метода.

• Этап 1. Рассматривается искусственная целевая функция, равная сумме искусственных переменных, которая минимизируется при помощи симплекс-метода. Другими словами, производится исключение искусственных переменных. Если минимальное значение вспомогательной задачи равно нулю, то все искусственные переменные обращаются в нуль и получается допустимое базисное решение начальной задачи. Далее реализуется этап 2. Если минимальное значение вспомогательной задачи положительное, то по крайней мере одна из искусственных переменных также положительная, что свидетельствует о противоречивости начальной задачи, и вычисления прекращаются.

• Этап 2. Допустимое базисное решение, найденное на первом этапе, улучшается в соответствии с целевой функцией исходной задачи ЛП на основе симплекс-метода, т.е. оптимальная таблица этапа 1 превращается в начальную таблицу этапа 2, и изменяется целевая функция.

9.6. Анализ чувствительности в линейном программировании

Решение практической задачи нельзя считать законченным, если найдено оптимальное решение. Дело в том, что некоторые параметры задачи ЛП (финансы, запасы сырья, производственные мощности) можно регулировать, что, в свою очередь, может изменить найденное оптимальное решение. Эта информация получается в результате выполнения анализа чувствительности. Анализ чувствительности позволяет оценить влияние этих параметров на оптимальное решение. Если обнаруживается, что оптимальное решение можно значительно улучшить за счет небольших изменений заданных параметров, то целесообразно реализовать эти изменения. Кроме того, во многих случаях оценки параметров получаются путем статистической обработки ретроспективных данных (например, ожидаемый сбыт, прогнозы цен и затрат). Оценки, как правило, не могут быть точными. Если удается определить, какие параметры в наибольшей степени влияют на значение целевой функции, то целесообразно увеличить точность оценок именно этих параметров, что позволяет повысить надежность рассматриваемой модели и получаемого решения.

9.7. Решение задач линейного программирования на эвм

Задачи линейного программирования могут быть решены с использованием многих пакетов прикладных программ, а именно:

• Statgraphics;

• LINDO;

• LINGO;

• MathCAD;

• Mathematica;

• MS Excel.

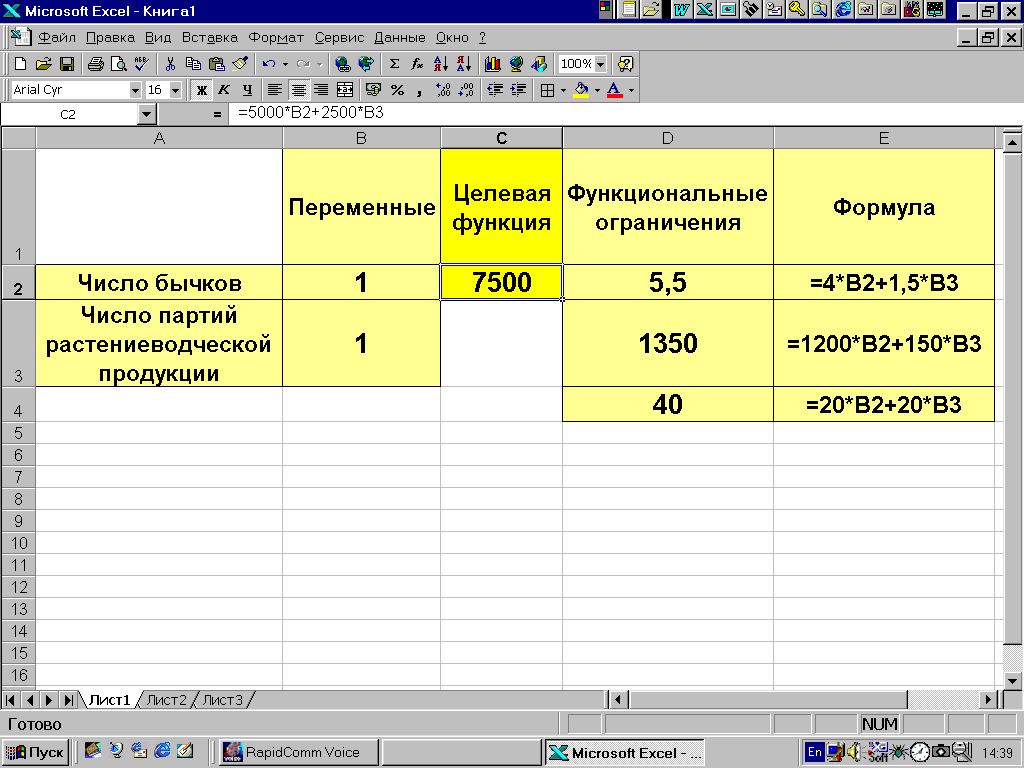
Рис. 9.2.

В качестве примера рассмотрим решение задачи примера 2.1 с использованием MS Excel. Для определенности в ячейки B1:B2, C1 и D1:D3 введем соответственно некоторые начальные значения двух переменных, целевую функцию и левые части функциональных ограничений. При этом необходимо переприсвоить значения x₁ на B2 и x₂ на B3 (рис. 9.2). Поиск осуществляется с помощью процедуры "поиск решения", которая вызывается из меню "сервис" (рис. 9.3). В появившемся окне (рис. 9.4) необходимо ввести:

• В поле "Установить целевую" введите ссылку на ячейку, содержащую целевую функцию (С1).

• Введите искомый результат в поле "Равной" (максимальное значение прибыли).

• В поле "Изменяя ячейки" введите ссылки на ячейки, содержащие переменные (B2:B3).

• В поле "Ограничения" введите с помощью кнопок "добавить", "изменить" и "удалить" ввести функциональные и областные ограничения.

• С помощью кнопки "Выполнить" запускаем процедуру на выполнение.

Результаты расчетов представлены на рис. 9.5.

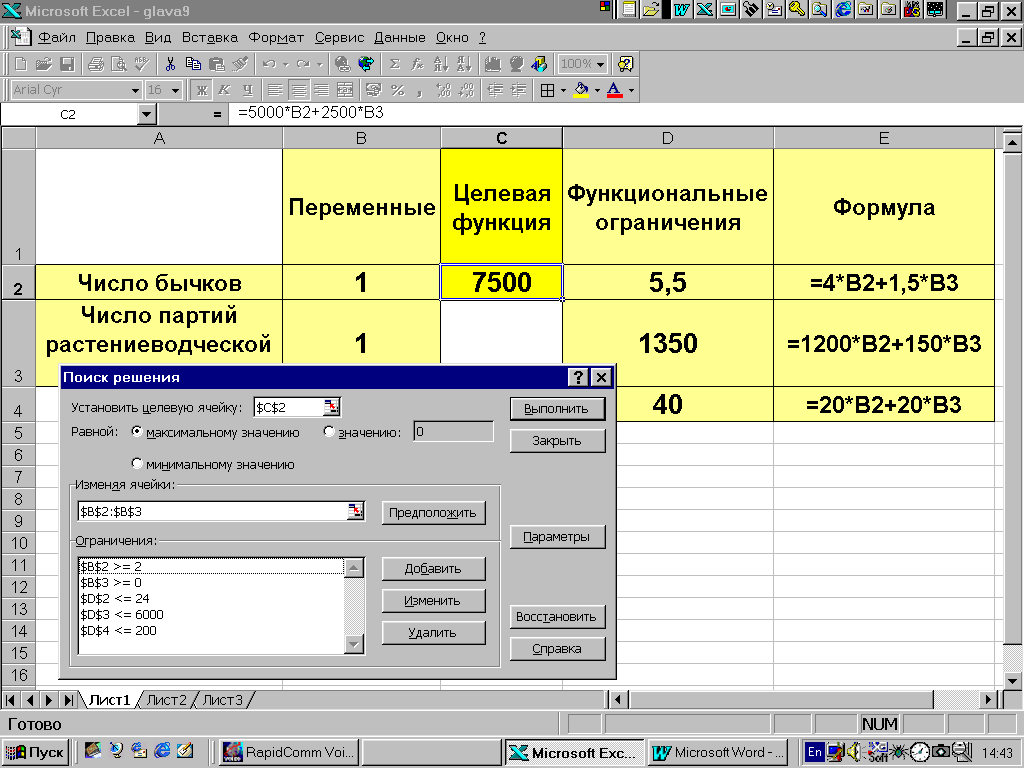
Рис. 9.3.

Рис. 9.4.

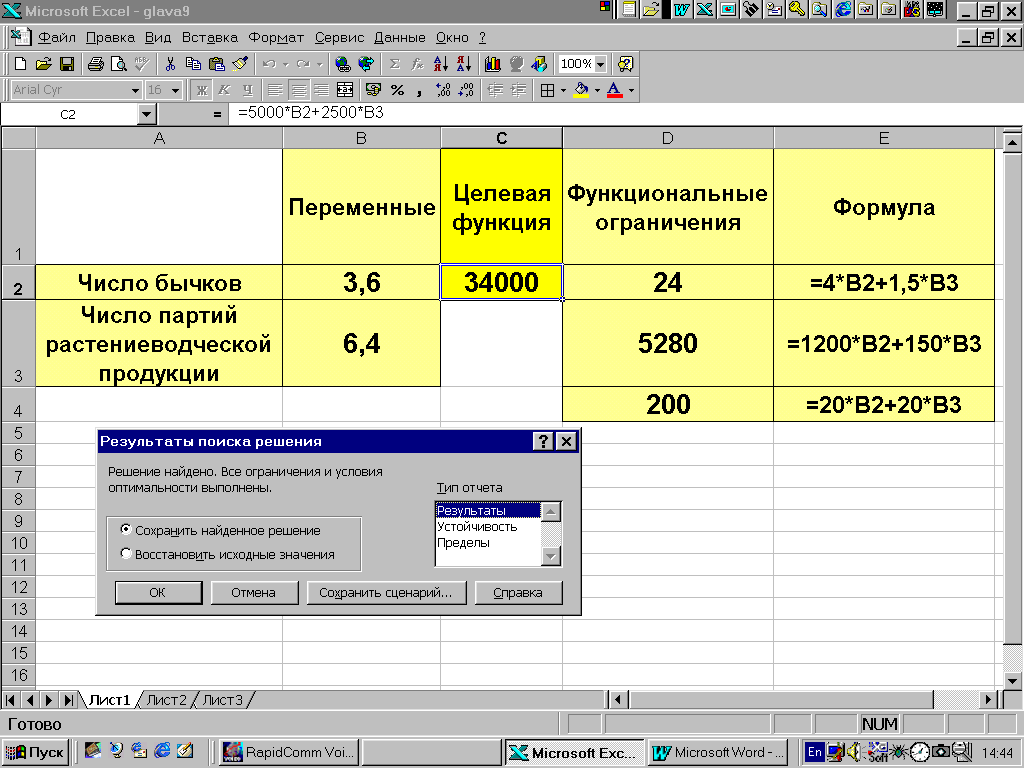
Рис.9.5.