Уравнение показательной кривой

Для вычисления коэффициентов a и b для уравнения

y = ab^x (7.17)

необходимо решить следующую систему нормальных уравнений:

(7.18)

Решение системы (7.18) относительно неизвестных a и b дает численные значения искомых коэффициентов:

ln , (7.19)

и

ln . (7.20)

Проверка значимости уравнения регрессии производится по F-критерию Фишера (7.8).

Пример 7.4. Найти уравнение регрессии, описывающее фактические значения высот по диаметрам в сосновом древостое, используя уравнение показательной кривой. Исходные данные и последовательность расчета с использованием MS Excel приведены на рис. 7.7. Полученное уравнение регрессии имеет вид y=10,351,024^x. При уровне значимости =0,05 F_ф=10,2>F_st=2,85. Следовательно, линейное уравнение регрессии адекватно описывает фактическое изменение высот от диаметров деревьев (рис.7.8).

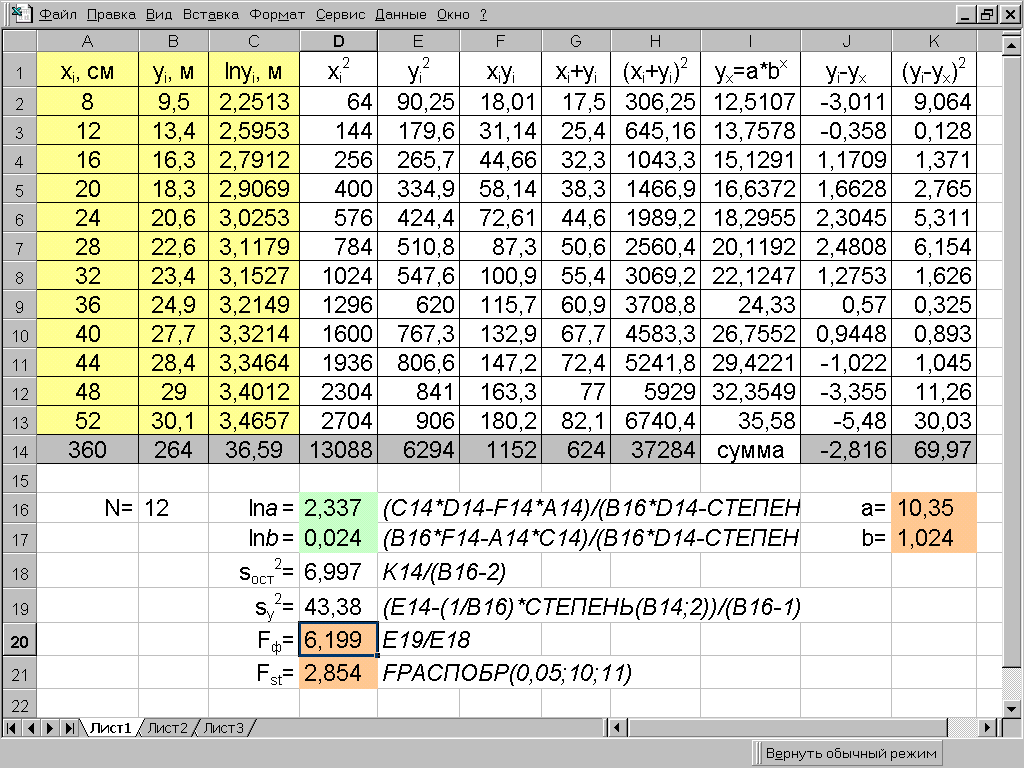
Рис. 7.7.

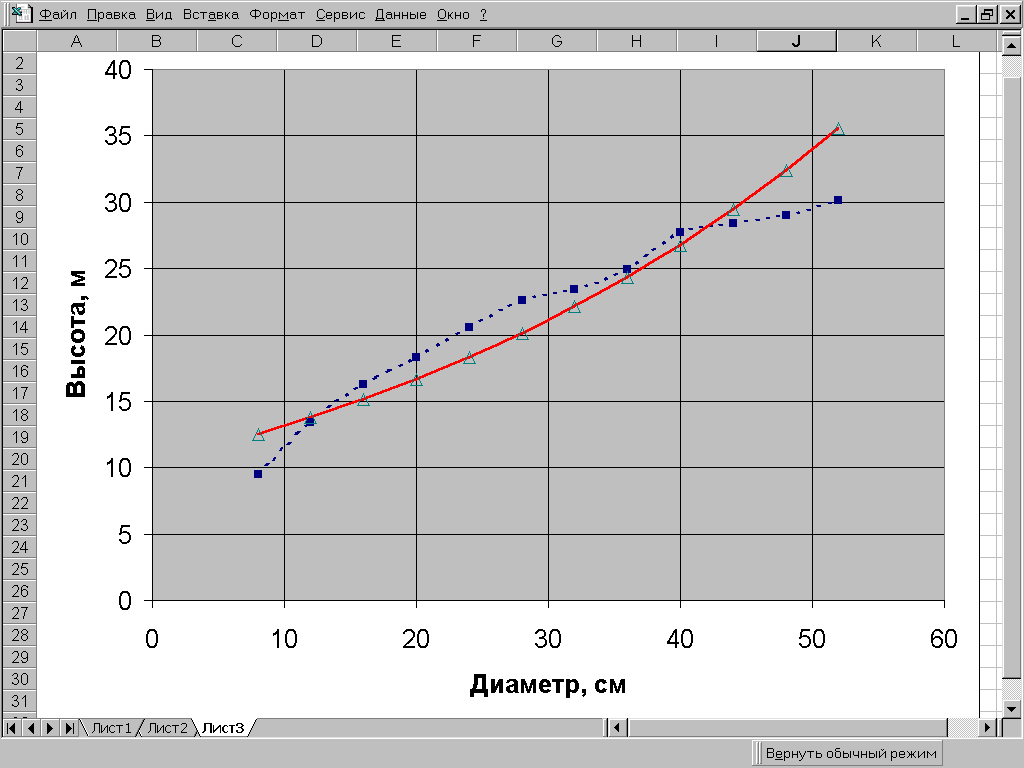
Рис. 7.8.

Окончательный выбор типа уравнения регрессии

На практике может сложиться ситуация, когда несколько уравнений адекватно предсказывают значения. В этом случае наиболее подходящим уравнением регрессии является то, которое характеризуется наибольшим фактическим значением F – критерия Фишера.

Пример 7.4. В табл. 7.1 приведены три уравнения регрессии, адекватно предсказывающие значения высот по диаметрам в сосновом древостое, т.е. F_ф > F_st. Взаимное сравнен ие значений F_ф показывает, что наилучшие результаты дает уравнение регрессии, выражаемое линейным уравнением с логарифмированием факторного признака (F_ф= 109,5).

Таблица 7.1

Вид уравнения регрессии	Дисперсия		F-критерий
	Общая	Остаточная	Fф	Fst
y = 8,64 + 0,445x	47,8	1,925	22,31	2,85
y = 30,965 - 197/x		5,305	8,176
y =-14,57+11,202 lnx		0,396	109,5
y=10,35*1,024x		6,997	6,199

При выборе уравнения регрессии следует оперировать погрешностями и ошибками, рассчитываемыми по следующим формулам:

абсолютная погрешность уравнения

(7.21)

относительная погрешность уравнения

(7.22)

систематическая ошибка

(7.23)

случайная ошибка

(7.24)

где

n - число наблюдений;

y_i - значение функции по уравнению;

y_j- фактическое значение функции.

Чем меньше величина погрешностей и ошибок, тем надежнее уравнение описывает исследуемую взаимосвязь. Формулы (7.21) – (7.24) следует так же использовать при оценке адекватности полученных моделей на материалах, не включенных в регрессионный анализ.

7.3. Сравнение линий регрессии

На практике часто требуется сравнить две линии регрессии, чтобы получить более надежное уравнение. Уравнения сравниваемых линий запишем в обычном виде:

y₁ = a₁ + b₁/x, (7.25)

y₂ = a₂ + b₂/x. (7.26)

Чтобы установить, носят ли отклонения между уравнениями случайный характер или выборки имеют различный характер зависимости y от x, необходимо проверить три нулевых гипотезы:

• о равенстве дисперсий ₁² и ₂²;

• о равенстве коэффициентов регрессии;

• о равенстве свободных членов.

1. Гипотезу H₀: ₁²=₂² проверяют по значению F-критерия на основе сравнения их выборочных оценок, т.е. значений остаточных дисперсий

F_ф = s₁²/s₂². (7.27)

Вычисленный F-критерий сравнивается с табличным F_st. Если F_ф>F_st при уровне значимости =0,01 и k₁=n₁-2 и k₂=n₂-2 степенях свободы, то H₀ отвергают. В противном случае проверка продолжается.

2. Гипотезу H₀: b₁=b₂ проверяют по значению t-критерия

. (7.28)

Если t_b>t_st при уровне значимости =0,01 и k=n₁+n₂-4 степенях свободы, то гипотезу о равенствах коэффициентов регрессии отвергают; в противном случае проверяют гипотезу о равенстве свободных членов a.

3. Гипотезу H₀: a₁=a₂ также проверяют по значению t-критерия. Если при =0,05 t_а<t_st, то гипотеза об идентичности линий регрессии принимается.

Зачастую в исследованиях наряду с получением частных взаимосвязей возникает необходимость выявления общих закономерностей, имеющих большую информативность и практическое использование. Как правило, решение поставленной задачи требует выполнения следующих процедур:

1. По статистическим критериям установить наличие или отсутствие криволинейности рассматриваемой взаимосвязи;

2. При наличии криволинейности произвести преобразование системы координат для линеаризации взаимосвязи;

3. Представить выявляемую взаимосвязь в долевых соотношениях отдельно по зависимой и независимой переменной;

4. Произвести статистический анализ сравнения линий регрессии, полученных из различных генеральных совокупностей.

Наличие криволинейности следует установить по значениям коэффициента корреляции и корреляционного отношения, используя формулу (6.8).

Линеаризация криволинейных линий регрессии осуществляется преобразованием системы координат типа: (y - lny), ( y - ), ( y - ),

(x - lnx), (x - 1/x), (x - x²) и др.

Долевая мера (y_{i /} y_Мx) каждого значения зависимой переменной (y_i) устанавливается как частное от его деления на величину зависимой переменной (y_Мx), соответствующей средней арифметической величине независимой переменной. Долевая мера (x_i/M_x) каждого значения независимой переменной (x_i) определяется как частное от его деления на среднюю арифметическую величину независимой переменной (M_x) конкретного ряда.

После выполнения указанных условий устанавливаем, имеют ли отклонения между линиями регрессии (A и B) случайный характер. Для этого необходимо проверить три нулевые гипотезы:

• о равенстве дисперсий _(A)² и _(B)²;

• о равенстве угловых коэффициентов b_(A) и b_(B);

• о совпадении обеих прямых (A) и (B).

1. Гипотезу H₀: _(A)²=_(B)² проверяют по значению F-критерия

F_ф = _(A)²/_(B)².

Вычисленный F-критерий сравнивается с табличным F_st. Если F_ф>F_st при уровне значимости =0,01 и k₁=n₁-2 и k₂=n₂-2 степенях свободы, то H₀ отвергают. В противном случае проверка продолжается.

2. Гипотезу Н₀: b_(A) = b_(B) проверяют по значению t-критерия

(7.29)

Если t_b1-b2 > t_st при уровне значимости =0,01 и k=n₁+n₂-4 степенях свободы, то гипотезу о равенстве угловых коэффициентов отвергают; в противном случае проверяют гипотезу о совпадении обеих прямых.

3. Гипотезу Н₀: t_(A)-(B) проверяют по значению t – критерия

(7.31)

Если t_(A)-(B) > t_st при уровне значимости =0,01 и k=n₁+n₂-4 степенях свободы, то гипотезу о совпадении обеих прямых отвергают.

Пример 7.5. Имеем данные процента всхожести семян (Y) под воздействием различных доз электрофизического воздействия (X) в виде двух статистических рядов (А) и (В)

Переменные первого ряда (A)		Кол-во, шт.		Переменные второго ряда (B)		Кол-во, шт.
Xi	Yi	n		Xi	Yi	n
1	42, 45, 43, 46, 42, 47, 46	7		1	48, 49, 47, 46, 49, 48, 47	7
2	50, 51, 53, 54, 52, 51, 55, 56	8		2	56, 57, 55, 58, 59, 60	6
3	62, 61, 63, 68, 69	5		3	68, 66, 65, 67, 68, 69, 68	7
4	72, 73, 74, 76, 78, 80	6		4	79, 80, 82, 78, 79, 81, 82	7
5	83, 82, 85, 86, 87, 89, 90	7		5	89, 90, 91, 87, 86, 85	6
6	92, 91, 93, 94, 95, 94, 91, 93	8		6	97, 98, 97, 96, 95, 97, 98, 99	8
7	96, 98, 99, 97, 99, 98, 98	7				41
		48

Расчет статистических критериев для сравнения линий регресии производим в следующей последовательности:

средняя арифметическая величина Y рядов (А) и (В)

Преобразование рядов и расчет вспомогательных показателей

ряд (A)

X	Yi – М								Yx	Yx*X	nx		nx*X	nx*Х2
1	-32	-29	-31	-28	-32	-27	-28		-207	-207	7	-29,57	7	7
2	-24	-23	-21	-20	-22	-23	-19	-18	-170	-340	8	-42,5	16	32
3	-12	-13	-11	-6	-5				-47	-141	5	-28,2	15	45
4	-2	-1	0	2	4	6			9	36	6	6	24	96
5	9	8	11	12	13	15	16		84	420	7	60	35	175
6	18	17	19	20	21	20	17	19	151	906	8	113,25	48	288
7	22	24	25	23	25	24	24		167	1169	7	167	49	343
С у м м а									-13	1843	48		194	986
Условное обозначение суммы									Y(1)	XY	n		X(1)	X(2)

ряд (B)

X	Yi – М								Yx	Yx*X	nx		nx*X	nx*Х2
1	-26	-25	-27	-28	-25	-26	-27		-184	-184	8	-23,0	8	8
2	-18	-17	-19	-16	-15	-14			-99	-198	6	-33,0	12	24
3	-6	-8	-9	-7	-6	-5	-6		-47	-141	7	-20,1	21	63
4	5	6	8	4	5	7	8		43	172	7	24,6	28	112
5	15	16	17	13	12	11			84	420	6	70,0	30	150
6	23	24	23	22	21	23	24	25	185	1110	7	158,6	42	252
С у м м а									-18	1179	41		141	609
Условное обозначение суммы									Y(1)	XY	n		X(1)	X(2)

для ряда (А)

для ряда (В)

для ряда (А)

для ряда (В)

для ряда (А)

для ряда (В)

угловой коэффициент

для ряда (А)

для ряда (В)

коэффициент корреляции

для ряда (А)

для ряда (B)

дисперсия

для ряда (А)

для ряда (B)

средняя арифметическая величина X ряда (А) и ряда (В)

для ряда (А)

для ряда (B)

средняя арифметическая величина Y ряда (А) и ряда (В)

для ряда (А)

для ряда (B)

Статистические показатели для расчета критериев F и t

48 4,04 73,73 201,92 9,6 10,1

41 3,44 73,56 124,1 10 4,6

1. Сравнение дисперсий линий регрессии

F критерий

. Так как рассчитанное значение F критерия очень близко, но все же больше теоретического при уровне значимости =0,01 делаем заключение о строгом различии дисперсий линий регрессии. Вместе с тем существенное различие дисперсий не указывает на отсутствие наложения усредненных теоретических прямых. Поэтому следует провести сравнение угловых коэффициентов линий регрессии.

2. Сравнение угловых коэффициентов линий регрессии

. Так как рассчитанное значение t- критерия меньше теоретического при уровне значимости =0,05 делаем заключение о равенстве угловых коэффициентов.

3. Сравнение линий регрессии на совпадение

. Так как рассчитанное значение t- критерия больше теоретического при уровне значимости =0,01, то делаем заключение о несовпадении линий регрессии.