7.2. Статистический анализ одномерных моделей
Вычисляя методами математического анализа минимум выражения (7.1), для одномерной модели, можно получить систему так называемых нормальных уравнений, в которых неизвестными величинами оказываются искомые параметры (численные коэффициенты) уравнения регрессии. Рассмотрим ряд нормальных уравнений, которые используются в лесном хозяйстве:
прямой линии;
гиперболы;
логарифмической кривой;
показательной кривой.
Расчет параметров других моделей (параболы, полиномов различных степеней и др.) производится аналогично.
Уравнение прямой линии
При вычислении параметров уравнения
y = a + bx (7.2)
в соответствии с (7.1) составляется выражение
.
(7.3)
Рассматривая a и b в качестве независимых переменных и приравнивая к нулю частные производные от левой части по этим переменным, получим два уравнения с двумя неизвестными:
(7.4)
после приведения системы к нормальной форме имеем:
(7.5)
Решение системы (7.5) относительно неизвестных a и b дает численные значения искомых коэффициентов:
(7.6)
и
.
(7.7)
Проверка значимости уравнения регрессии производится по F-критерию Фишера. При этом общая дисперсия sy2 сравнивается с остаточной sост2:
Fф = sy2 /sост2 (7.8)
Для принятого уровня значимости Fф сравнивается с табличным значением Fst и делается вывод об адекватности описания уравнением рассматриваемой взаимосвязи.
Пример 7.1. Получить уравнение регрессии, описывающее фактические значения высот по диаметрам в сосновом древостое, используя линейную модель. Исходные данные и последовательность расчета с использованием MS Excel приведены на рис. 7.1. Полученное уравнение регрессии имеет вид y = 8,641 + 0,445x. При уровне значимости =0,05 Fф > Fst. Следовательно, линейное уравнение регрессии адекватно описывает фактическое изменение высот от диаметров деревьев (рис.7.2). При этом значение Fф=22,31 указывает на то, что уравнение прямой линии в 22 раза лучше описывает рассматриваемую взаимосвязь чем среднее значение зависимой переменной.
Рис. 7.1.
Уравнение гиперболы
Для вычисления коэффициентов a и b гиперболической зависимости:
y = a + b/x (7.9)
необходимо решить следующую систему нормальных уравнений:
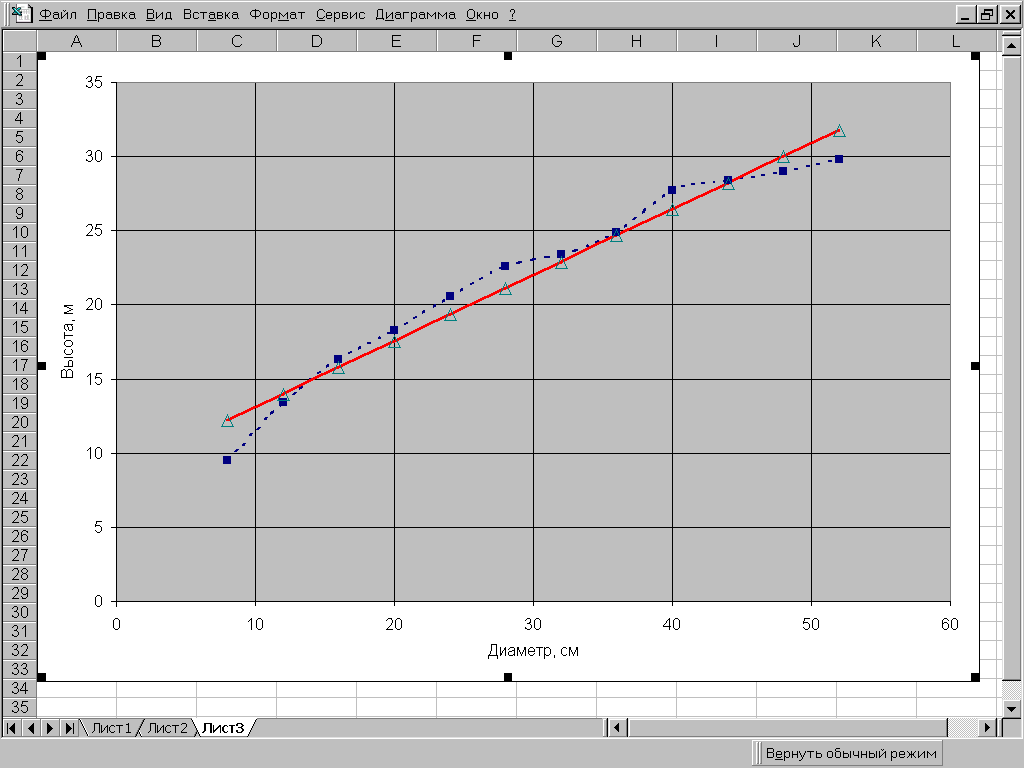
Рис. 7.2.
(7.10)
Результатом решения системы нормальных уравнений являются следующие выражения:
(7.11)
и
.
(7.12)
Проверка значимости уравнения регрессии производится по F-критерию Фишера, формула (7.8).
Пример 7.2. Найти уравнение регрессии, описывающее фактические значения высот по диаметрам в сосновом древостое, используя гиперболическую модель. Исходные данные и последовательность расчета с использованием MS Excel приведены на рис. 7.3. Полученное уравнение регрессии имеет вид y = 30,965 - 197/x. При уровне значимости =0,05 Fф > Fst. Следовательно, гиперболическое уравнение регрессии адекватно описывает фактическое изменение высот от диаметров деревьев (рис.7.4).
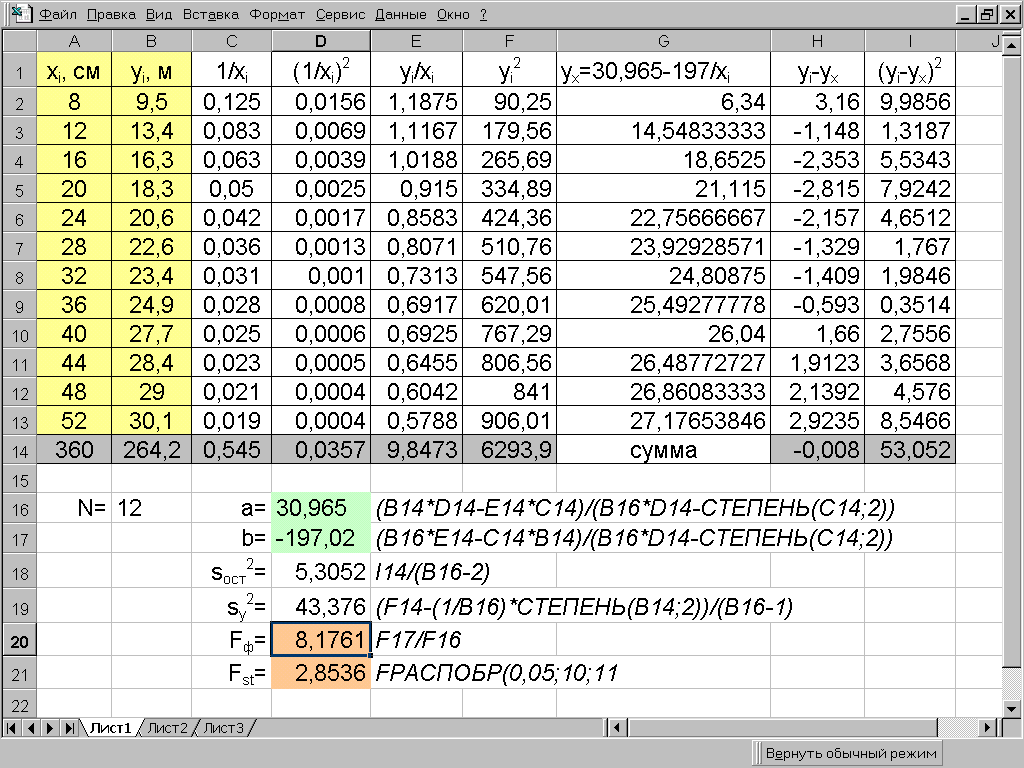
Рис. 7.3.
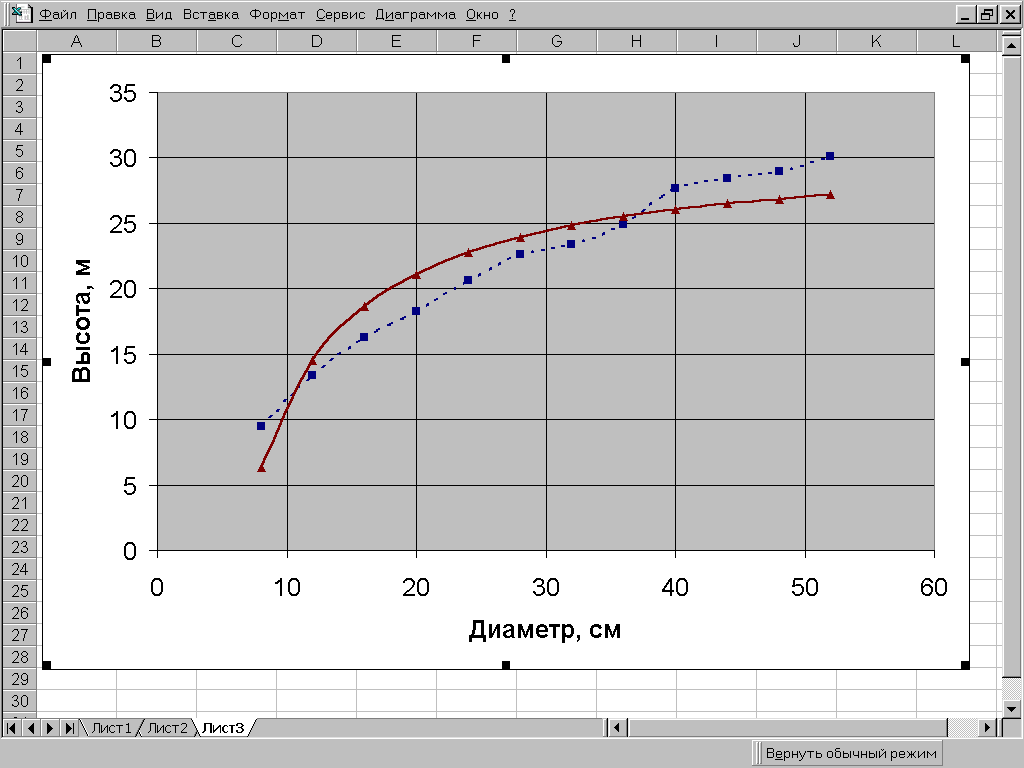
Рис. 7.4.
Линейное уравнение с логарифмированием факторного признака
Для вычисления коэффициентов a и b для уравнения прямой с логарифмированием факторного признака
y = a + b lnx (7.13)
необходимо решить следующую систему нормальных уравнений:
(7.14)
Решение системы (7.14) относительно неизвестных a и b дает численные значения искомых коэффициентов:
(7.15)
и
.
(7.16)
Проверка значимости уравнения регрессии производится по F-критерию Фишера (7.8).
Пример 7.3. Найти уравнение регрессии, описывающее фактические значения высот по диаметрам в сосновом древостое, используя линейную модель с логарифмированием факториального признака. Исходные данные и последовательность расчета с использованием MS Excel приведены на рис. 7.5. Полученное уравнение регрессии имеет вид y=-14,57+11,202lnx. При уровне значимости =0,05 Fф>Fst. Следовательно, линейное уравнение регрессии адекватно описывает фактические изменение высот от диаметров деревьев (рис.7.6).
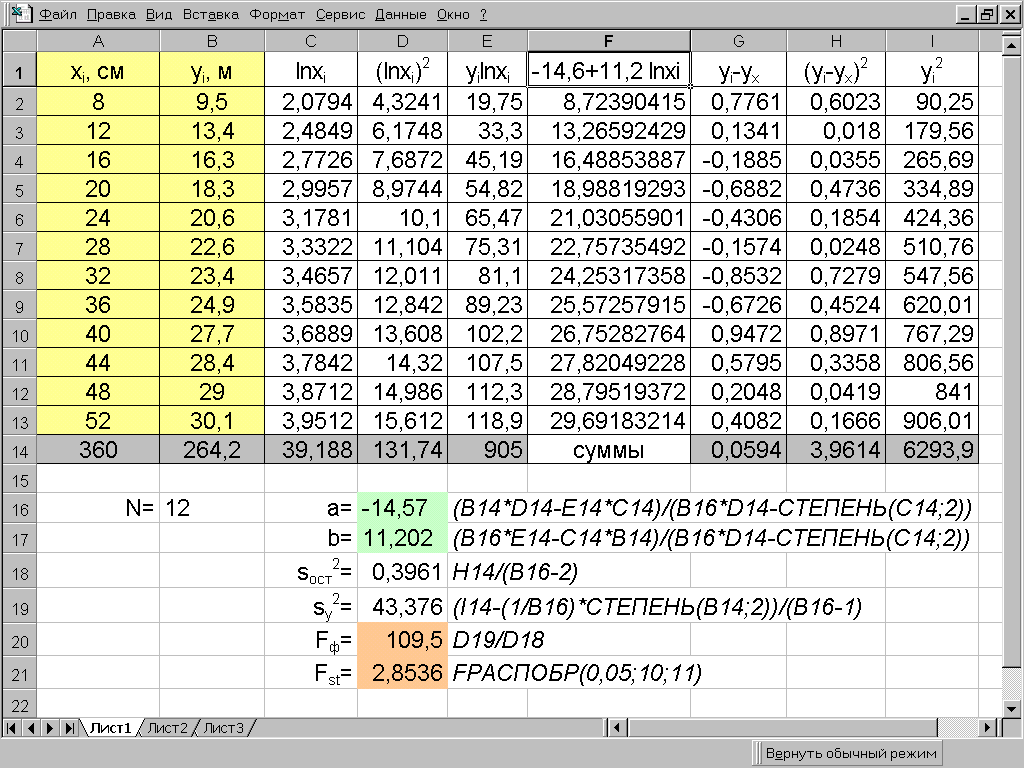
Рис. 7.5.
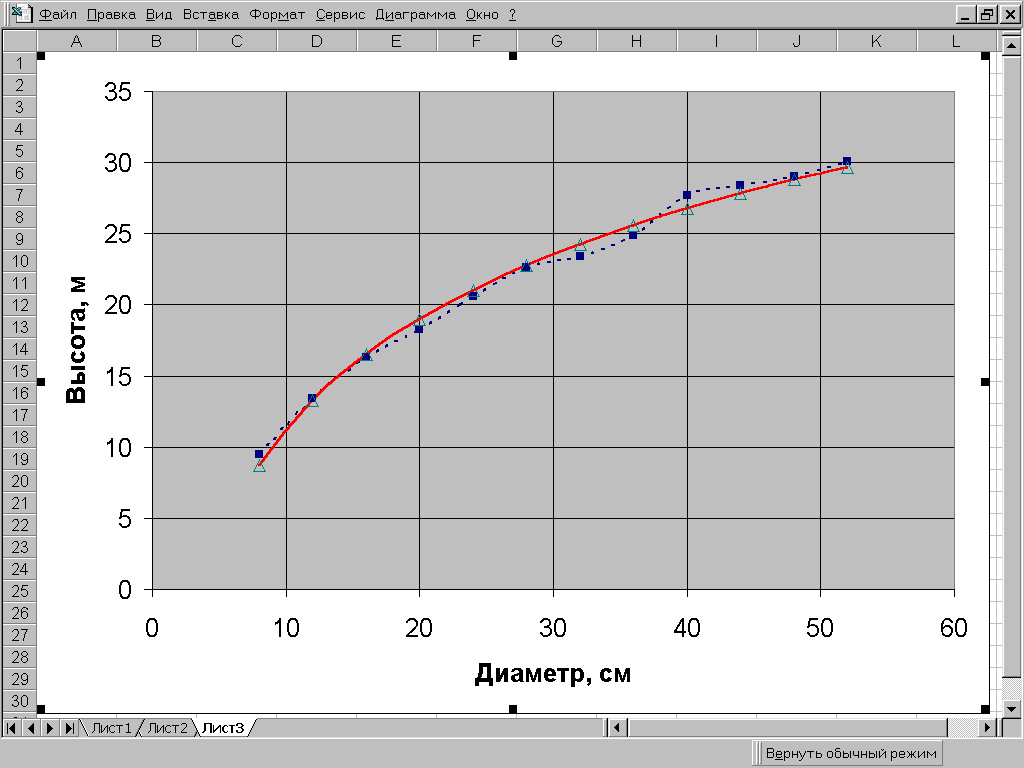
Рис. 7.6.