6.2. Коэффициент корреляции

Корреляционный анализ имеет своей задачей количественное определение тесноты связи между признаками при парной связи и между результативным (изменяющимся под действием других, связанных с ним признаков) и множеством факторных признаков (обуславливающих изменение результативных признаков) при многофакторной связи. Теснота связи количественно выражается величиной коэффициентов корреляции.

Парный коэффициент корреляции, являясь численной характеристикой линейной связи между признаками, для которой уравнение регрессии имеет вид

y = a + bx , (6.1)

где

a и b – коэффициенты,

численно выражается отношением числа факторов, действующих на изменение обоих признаков к общему числу факторов

, (6.2)

где

N – число наблюдений;

s_x ,s_y – средние квадратические отклонения распределений x и y.

Коэффициент корреляции r может принимать значения от +1 до –1. При полной прямой корреляции r=+1, при полной обратной - r=-1. При r0 прямолинейная связь отсутствует (криволинейная связь при этом может наблюдаться). Обычно считают, что при r=0,1…0,3 связь слабая, при r=0,3…0,7 – средняя, при r>0,7 – сильная или тесная.

Эмпирический коэффициент корреляции, как и любой другой выборочный показатель, служит оценкой своего генерального параметра  и как величина случайная сопровождается ошибкой:

. (6.3)

Отношение выборочного r к своей ошибке служит критерием (t-критерий Стьюдента) для проверки нулевой гипотезы H₀: =0. При этом определяется фактическое значение критерия t_ф:

. (6.4)

Вычисленное t_ф сравнивается с критерием t_st, которое определяется с учетом значения уровня значимости  и числа степеней свободы k (см. п. 4.4). Если t_ф>t_st, то нулевую гипотезу отвергают на принятом уровне значимости.

Пример 6.3. Рассмотрим зависимость текущего прироста по запасу от относительной полноты древостоя. Требуется определить тесноту связи между этими двумя признаками. Результаты наблюдений и их обработка приведены на рис. 6.2.

Значение коэффициента корреляция r=0,923 указывает на наличие положительной тесной корреляционной связи между относительной полнотой древостоя и его текущим приростом. Значимость коэффициента корреляции оценивается t_ф=10,2. Критическое значение при числе свободы k=N-2=18 и уровне значимости =0,05 соответствует t_st=2,101. Следовательно, нулевую гипотезу об отсутствии взаимосвязи отвергаем на принятом уровне значимости, т.к. t_ф > t_st.

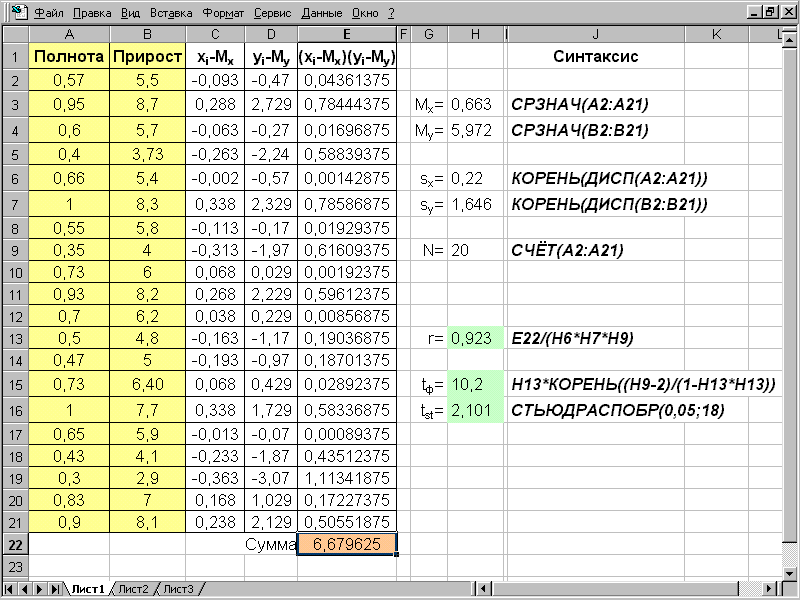
Рис. 6.2.

6.3. Корреляционное отношение

Корреляционное отношение  характеризует тесноту зависимости между случайными величинами при любой форме связи. Вычисляется как отношение среднего крадратического отклонения групповых средних S_yx к общему среднему квадратическому отклонению sy

_yx = s_yx / s_y , (6.5)

где

; .

Здесь

M_y – общее среднее арифметическеое;

M_yi – групповое среднее арифметическое;

f_i – частота ряда x.

Корреляционное отношение показывает, какую часть общей вариации результативного признака составляет вариация частных средних этого признака. Корреляционное отношение имеет всегда положительное значение, которое изменяется от 0 до 1. Когда групповые средние одинаковы, то =0 и связь отсутствует. В случае строгой прямолинейной связи (все точки лежат на одной прямой) =r=1. Чем ближе  к 1, тем связь теснее. Чем больше различие между  и r, тем связь более криволинейна. В предельном случае, когда связь строго криволинейна и кривая проходит через групповые средние так, что s_yх = s_y, то =1, а r=0.

При малом числе наблюдений показатель  недостаточно надежен, поэтому следует вводить корректирование по формуле

² = 1 – (1 - ²)[(N-1)(N-m)], (6.6)

где

m – число групп.

Отношение выборочного  к своей ошибке служит критерием (t-критерий Стьюдента) для проверки нулевой гипотезы. При этом определяется фактическое значение критерия t_ф:

. (6.7)

Если t_ф>t_st, то нулевую гипотезу отвергают на принятом уровне значимости .

Пример 6.4. Требуется вычислить корреляционное отношение при малом числе наблюдений между 10 наблюдениями диаметра деревьев и объемом. Исходные данные и последовательность вычислений приведены на рис. 6.3.

Полученное скорректированное корреляционное отношение =0,978 свидетельствует о тесной связи. Достоверность оценки корреляционного отношения проверено по t-критерию Стьюдента для k=N-2=8 и =0,05 (см. рис. 6.3). Получено, что t_ф=13,34>t_st=2,306. Следовательно, можно считать доказанным, что между диаметром деревьев и их объемом существует очень тесная взаимосвязь.

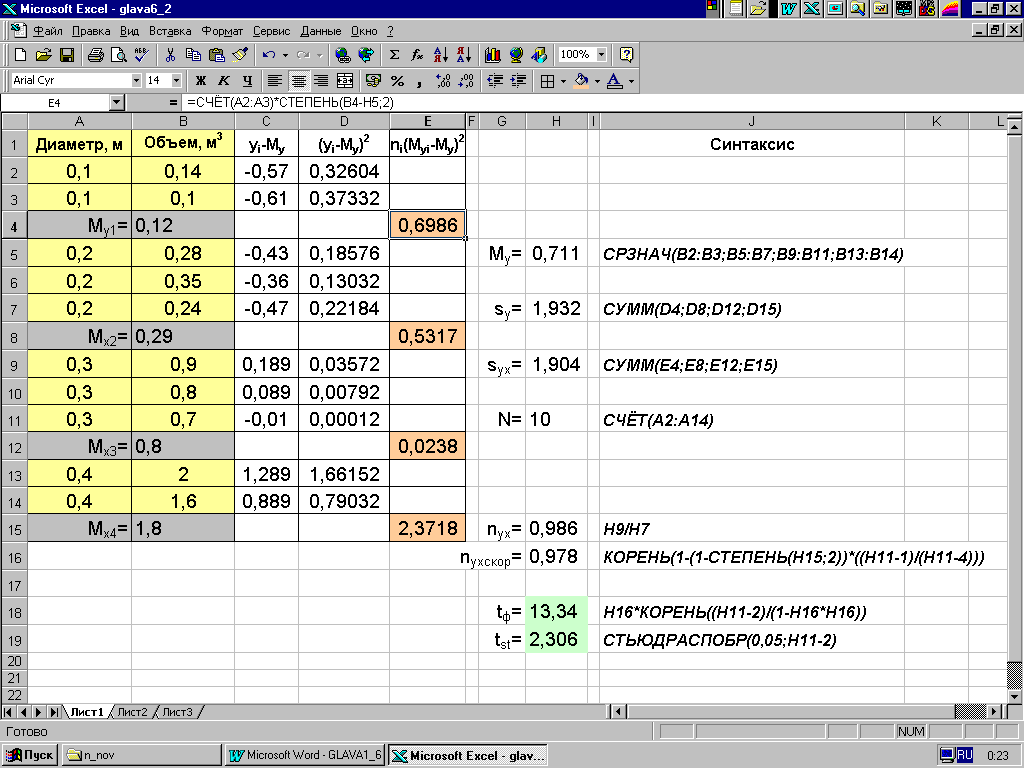
Рис. 6.3.