5.4. Использование ms Excel для проведения дисперсионного анализа
Для вызова программы проведения дисперсионного анализа необходимо выбрать команду "Анализ данных" в меню "Сервис". В списке "Инструменты анализа" (рис. 5.3) выбираем одну из строк:
"Однофакторный дисперсионный анализ";
"Двухфакторный дисперсионный анализ с повторениями";
"Двухфакторный дисперсионный анализ без повторений".
Рис. 5.3.
5.4.1. Однофакторный дисперсионный анализ
Для определенности рассмотрим решение в среде MS Excel задачи из примера 5.1 с применением процедуры «Однофакторный дисперсионный анализ». В появившемся диалоговом окне (рис. 5.4) последовательно вводим:
cсылку на диапазон, содержащий анализируемые данные (B2:G9);
установку переключателеля в положение «По столбцам» или «По строкам» (в нашем случае) в зависимости от расположения данных во входном диапазоне;
уровень значимости =0,05, необходимый для оценки критических параметров F-статистики. Уровень связан с вероятностью возникновения ошибки типа I (опровержение верной гипотезы);
отметку, куда поместить результаты: на новый лист в текущей книге (в нашем случае он назван «Однофакторный анализ» или на первый лист новой книги.
На рис. 5.5 приведены результаты, которые полностью соответствуют результатам, полученным при решении примера 5.3 (см. рис. 5.1).
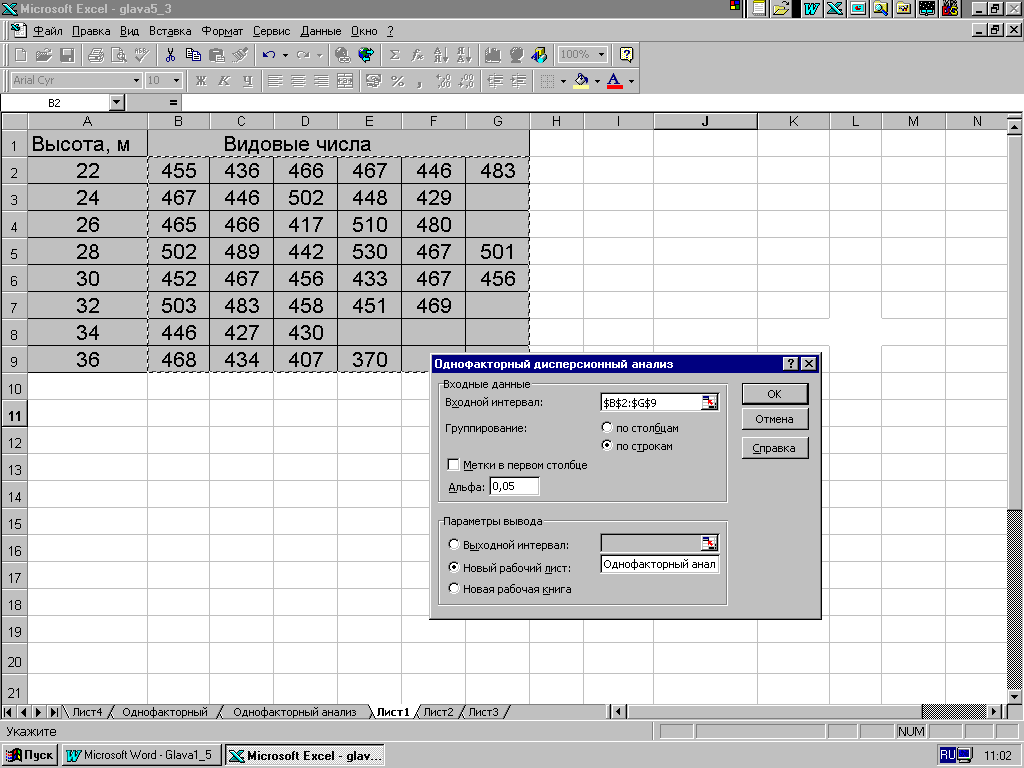
Рис. 5.4.
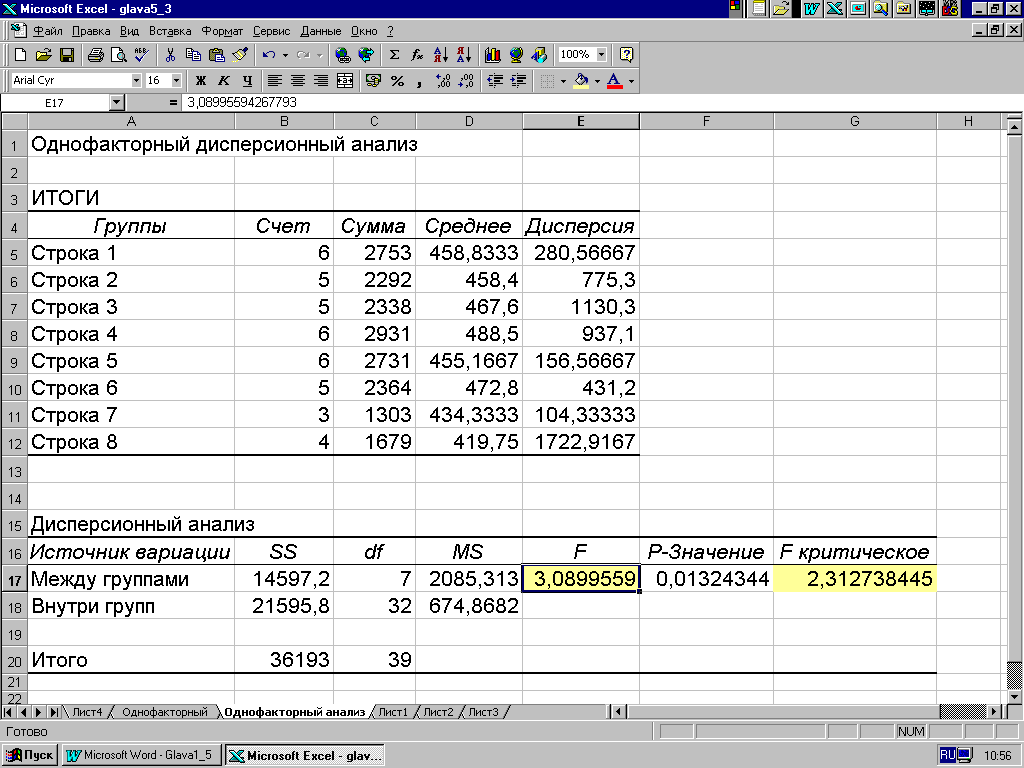
Рис. 5.5.
5.4.2. Двухфакторный дисперсионный анализ без повторения
Для определенности рассмотрим решение в среде MS Excel задачи из примера 5.4 с применением процедуры "Двухфакторный дисперсионный анализ без повторения". В появившемся диалоговом окне (рис. 5.6) последовательно вводим:
cсылку на диапазон, содержащий анализируемые данные (B2:F5);
уровень значимости =0,05, необходимый для оценки критических параметров F-статистики. Уровень связан с вероятностью возникновения ошибки типа I (опровержение верной гипотезы);
пометку, куда поместить результаты: на новый лист в текущей книге (в нашем случае он назван «Двухфакторный анализ») или на первый лист новой книги.
На рис. 5.7 приведены результаты, которые полностью соответствуют результатам, полученным ранее при решении примера 5.4 (см. рис. 5.2).
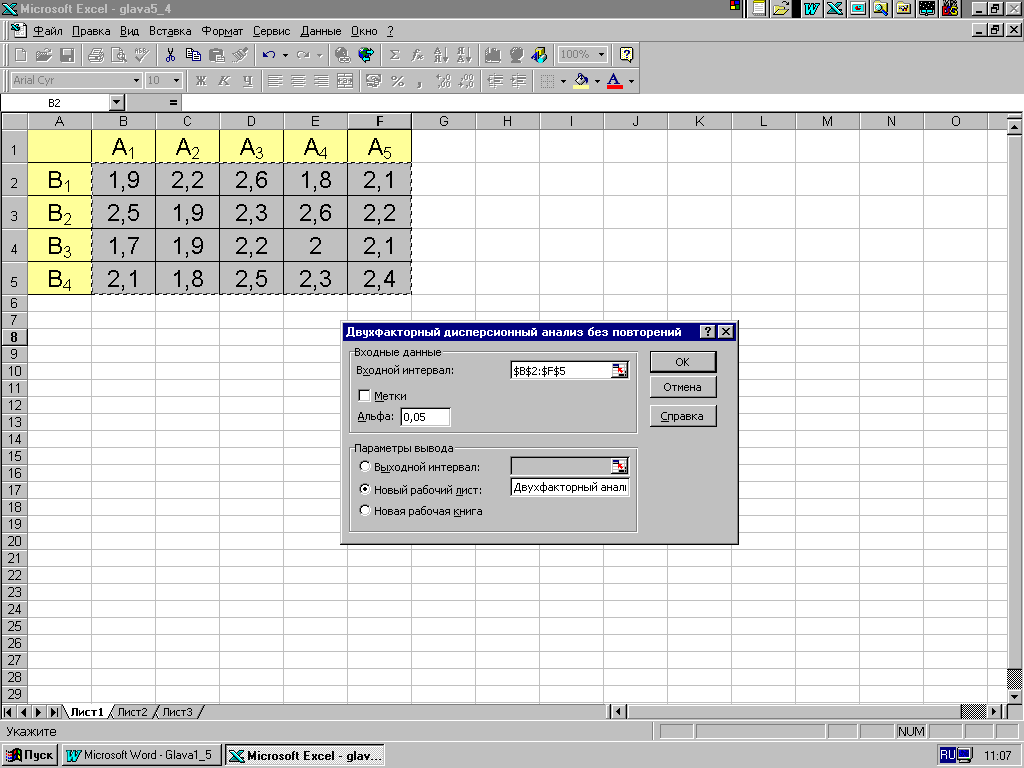
Рис. 5.6.
Рис. 5.7.
5.5. Контрольные вопросы и задания
В чем заключается сущность дисперсионного анализа?
Охарактеризуйте виды статистических комплексов, используемых в дисперсионном анализе.
Приведите схемы подготовки опытных материалов к расчетам однофакторных и двухфакторных комплексов.
Приведите примеры статистического доказательства существенности влияния независимых переменных на результативный признак.
Глава 6.
Корреляционный анализ
6.1. Постановка задачи
Отличительной чертой лесохозяйственных объектов является многообразие признаков, характеризующих каждый из них. Так, дерево можно характеризовать возрастом, размерами, объемом, другими различными таксационными показателями. Имея однородную совокупность объектов, можно изучить распределение их по любому из их признаков. Достаточно часто можно усмотреть известную связь между вариациями по различным признакам. Например, чем больше размеры дерева, тем обычно больше объем его стволовой части.
В простейшем случае связь между двумя переменными величинами строго однозначна. Например, вес образцов, сделанных из одного и того же материала, полностью определяется их объемом. Такого рода зависимость принято называть функциональной. Для лесохозяйственных объектов связь обычно бывает менее «жесткой»: объекты с одинаковым значением одного признака имеют, как правило, разные значения по другим признакам. Такую связь между вариациями разных признаков называют корреляцией (дословный перевод: соотношение) между признаками.
Пример 6.1. Измерение диаметров и высот 250 экземпляров сосны дало результаты:
Диаметр, см |
21 |
27 |
19 |
26 |
… |
18 |
27 |
Высота, м |
22 |
46 |
21 |
31 |
… |
20 |
45 |
Каждый из этих рядов может быть обработан отдельно. Но если желательно установить наличие и характер корреляции между обоими признаками (диаметром и высотой), то следует разнести обследованные экземпляры (точнее, соответствующие численные значения) в одну общую таблицу. Это будет, естественно, двумерная таблица. Но так как число особей в данном случае велико, то необходимо провести группировку данных. Диаметры принимают значения от 15 до 50 см, так что интервал 50 - 15 = 35 можно разбить на 7 частей (разрядов) по 5 см в каждом; впрочем, можно было бы взять 9 разрядов по 4 см. Высоты оказались в пределах от 18 до 28 м, поэтому произведем группировку по 10 разрядам.
Результат такой группировки представлен в табл. 6.1. Первое дерево(диаметр- 22 см, высота -19,3 м) попало в клетку на пересечении второй строки (диаметры от 17,5 до 22,5 см, т. е. середина разряда - 20 см) и второго столбца (высота от 18,5 до 19,5 м, середина разряда - 19 м), т. е. в число 3; второе - в клетку на пересечении пятой строки и седьмого столбца (в число 6) и т. д.
Таблица 6.1
Диаметр, см |
Высота, м |
||||||||||
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
nx |
|
15 |
|
1 |
6 |
4 |
3 |
|
|
|
|
|
14 |
20 |
1 |
3 |
15 |
29 |
20 |
8 |
|
|
|
|
76 |
25 |
|
1 |
8 |
18 |
49 |
20 |
6 |
1 |
|
|
103 |
30 |
|
|
1 |
4 |
5 |
12 |
8 |
5 |
|
|
35 |
35 |
|
|
|
|
1 |
3 |
6 |
4 |
1 |
|
15 |
40 |
|
|
|
|
|
|
1 |
3 |
2 |
|
6 |
45 |
|
|
|
|
|
|
|
|
1 |
1 |
2 |
ny |
1 |
5 |
30 |
55 |
78 |
43 |
21 |
13 |
4 |
1 |
250 |
Уже по виду таблицы (ее называют корреляционной решеткой) можно сделать заключение о наличии явной корреляции (связи) между диаметром дерева и его высотой. Действительно, толстые деревья, как правило, более высоки, чем тонкие. Однако мы видим, что однозначного соответствия между диаметром и толщиной все же нет - некоторые из тонких деревьев оказались выше, чем отдельные толстые деревья. Такая "размазанность" корреляции чрезвычайно характерна для биологических объектов, развитие которых определяется сложным переплетением многих факторов.
Важно отметить, что установление корреляции между признаками само по себе еще не дает оснований делать какие-либо заключения о причинно-следственных связях между ними. Так, в данном примере ни один из признаков не может считаться влияющим непосредственно на второй; верней всего, оба они обуславливаются в основном третьим признаком - возрастом дерева. В некоторых случаях корреляция вызывается тем, что один признак является следствием другого, например, корреляция между объемом ствола дерева и запасом на единицу площади. Задачей предстоящего анализа будет лишь установление самого факта корреляции и отыскание подходящих численных характеристик для выражения степени этой корреляции.
В случае с не сгруппированной совокупностью данных может быть получено наглядное представление о наличии или отсутствии корреляции путем построения так называемого корреляционного поля.
Пример 6.2. Измерения массы стволов (x) и массы ветвей (у) у 16 деревьев дали результаты, представленные на рис. 6.1. Нанося точки на графике в выбранном масштабе, получаем точечную диаграмму. Вытянутость корреляционного поля в диагональном направлении свидетельствует о несомненном наличии корреляции между обоими признаками.
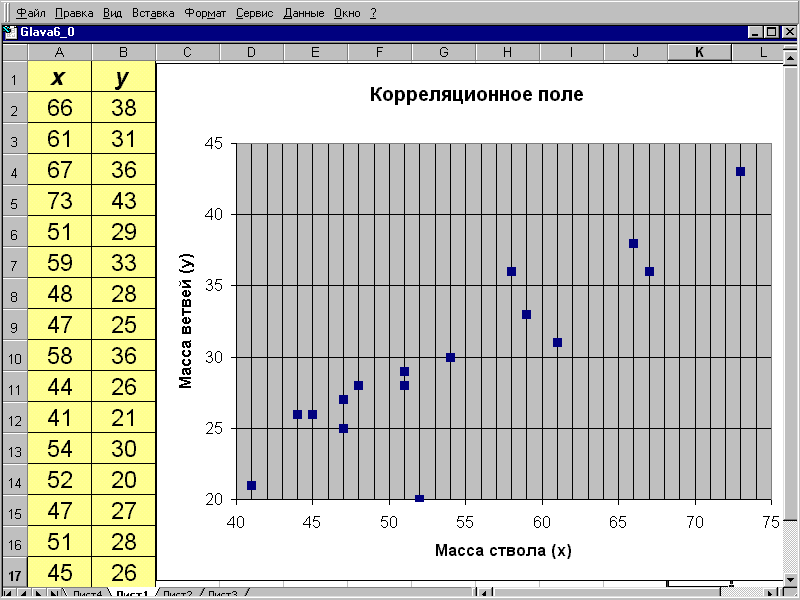
Рис. 6.1.
Если число вариант велико, то корреляционное поле часто имеет вид более или менее правильного эллипса со сгущением точек в центре и сравнительно редким их расположением на периферии; отклонение осей эллипса от координатных направлений указывает на наличие корреляции. Вытянутость же эллипса является менее объективным показателем, ибо она в большей мере зависит от принятых масштабов по осям координат.