5.3. Двухфакторный комплекс

Рассмотрим влияние двух факторов: А, градации (или уровни) которого обозначены A_i (i=1…m) и B с уровнями B_j (j=1…k). При этом каждое наблюдение можно обозначить через x_ij, где i - уровень фактора A, j - номер наблюдения. Исходные данные удобно представить в виде табл. 5.2.

Таблица 5.2

Bj	Ai				MjB
	A1	A2	…	Am
B1	x11	x12	…	x1m	M1
B2	x21	x22	…	x2m	M2
…	…	…	…	…	…
Bk	xk1	xk2	…	xkm	Mk
MiA	M1	M2	…	Mm

Общая схема дисперсионного анализа двухфакторных комплексов в принципе не отличается от описанных схем однофакторного дисперсионного анализа. Анализ двухфакторных комплексов не меняет, а лишь несколько усложняет расчеты, поскольку наряду с действием каждого фактора в отдельности приходится учитывать и их совместное действие на результативный признак. Однако следует строго выполнять требование независимости факторов. Нельзя подвергать дисперсионному анализу корреляционно связанные признаки, такие, например, как высота дерева и объем его стволовой части.

В двухфакторных дисперсионных комплексах определяются четыре дисперсии.

1. Общая дисперсия равна сумме центральных отклонений вариант x_ij от общей средней по комплексу M:

s₀²= (x_ij – M)². (5.6)

2. Дисперсия по первому фактору (A) равна сумме взвешенных квадратов центральных отклонений частных средних по градациям первого фактора от общей средней по всему комплексу:

s_A²= (M_iA –M)², (5.7)

где

m - число наблюдений по фактору А одной градации;

M_iA - частные средние значения по градациям фактора A;

M - общее среднее значение для всего комплекса.

3. Дисперсия по второму фактору (B) равна сумме взвешенных квадратов центральных отклонений частных средних по градациям второго фактора от общей средней по всему комплексу:

s_B²= (M_jB–M)², (5.8)

где

k - число наблюдений по фактору B одной градации;

M_jB - частные средние значения по градации фактора В;

M - общее среднее значение для всего комплекса.

4. Дисперсия по сочетанию градаций s_AB² дает меру разнообразия эффектов второго признака (его градаций) при разных градациях первого признака.

Так как в ортогональных (равномерных и пропорциональных) дисперсионных комплексах все дисперсии находятся в определенной связи, то сумма частных дисперсий, рассчитанных независимо, равна общей дисперсии:

s_AB² = s₀² - s_A² - s_B², (5.9)

где

s₀² - общая дисперсия;

s_A² - дисперсия по первому фактору;

s_B² - дисперсия по второму фактору.

Отношения (5.10) и (5.11) используют в качестве статистической характеристики критерия.

F = (5.10)

и

F = (5.11)

Если вычисленное значение F меньше табличного при уровне значимости , то гипотезу об отсутствии влияния фактора А или B принимают. Стандартные значения критерия F приведены в приложениях 6 и 7.

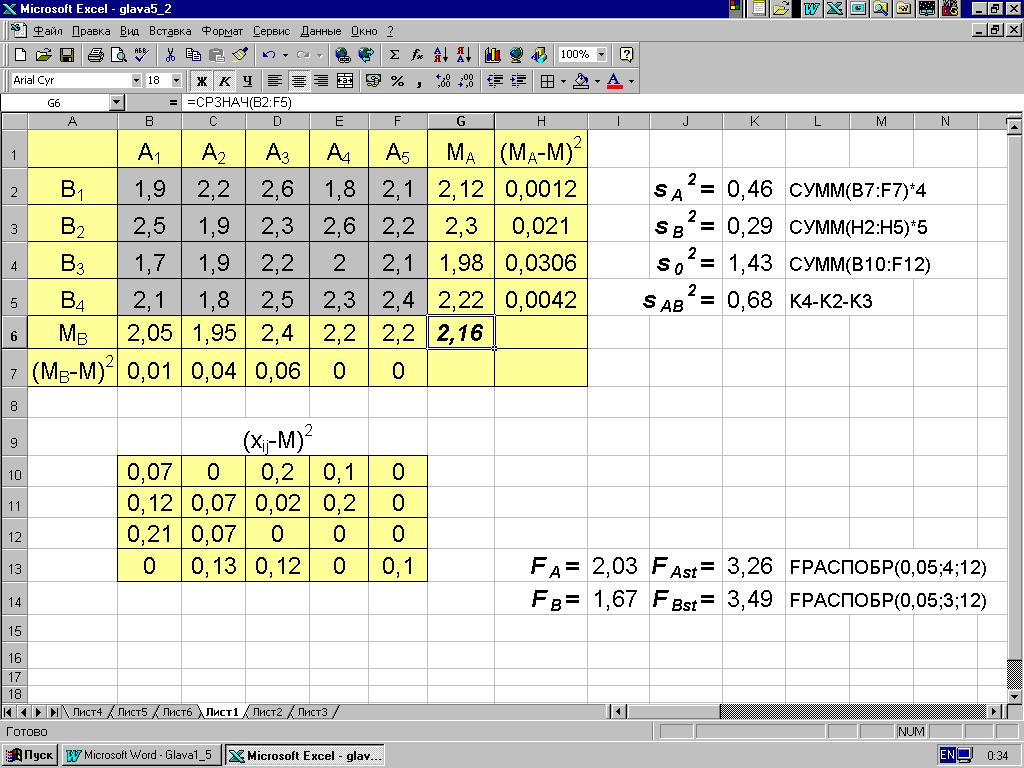
Рис. 5.2.

Пример 5.4. Рассмотрим результаты влияния пяти различных удобрений (фактор А) и четырех типов почв (фактор В) на прирост древостоя, представленные в MS Excel (рис. 5.2). Требуется установить, есть ли основание считать, что прирост на разных типах почвы не зависит от вида удобрения и что эффективность разных удобрений различна независимо от типа почвы. На рис. 5.2 приведены все необходимые расчеты. Поскольку для обоих факторов при уровне значимости =0,05 и соответствующих степенях свободы F_ф<F_st (получены с помощью функции FРАСПОБР), то следует считать, что нулевая гипотеза не отвергается, то есть вариации могли иметь случайное происхождение.