5.2. Однофакторный комплекс

Изучается зависимость некоторой величины от меняющегося фактора А, градации (или уровни) которого обозначены A_i. Тогда каждое наблюдение можно обозначить через x_ij, где i - уровень фактора A, j - номер наблюдения. Исходные данные удобно представить в виде табл. 5.1.

Таблица 5.1

Уровни фактора Ai	Результаты измерений	Средние по факторам
A1	x11 x12 … x1m	M1
A2	x21 x22 … x2m	M2
…	…	…
Ak	Xk1 xk2 … xkm	Mk

В табл. 5.1 k строк (или групп) - по числу уровней фактора А, в каждой группе m_i наблюдений (число наблюдений неодинаково); при равном числе наблюдений подход не меняется, но приводимые ниже формулы несколько упрощаются, так как все m_i равны m. Для подготовки данных к анализу образуем суммы квадратов:

s₀²= (x_ij—M)²; (5.1)

s_m²= m_i(x_ij—M)²; (5.2)

s_b²= (x_ij—M_i)², (5.3)

где

s₀² - общая сумма квадратов всех наблюдений от общей средней M;

s_m² - cумма квадратов отклонений групповых средних M_i от общей средней M, взвешенной через число наблюдений по группам:

s_b² -cумма квадратов отклонений внутри групп (от групповых средних).

Простые преобразования позволяют разложить первую сумму на две другие:

s₀² = s_m² + s_b² . (5.4)

Формула (5.4) является основой дисперсионного анализа. Рассмотрим оценки дисперсий, связанных с введенными суммами. Сумма s₀² связана с оценкой общей дисперсии изучаемого признака, если ее разделить на число степеней свободы N - 1, где N - число наблюдений. По сумме s_m² можно оценить дисперсию между уровнями факторов A_i - межгрупповую дисперсию. Число степеней свободы k - 1. Сумма s_b² позволяет оценить дисперсию внутри групп (или остаточную). Так как оценка дисперсии внутри каждой из групп связана с m_i - 1 степенью свободы, то общее число степеней свободы k(m_i - 1) = N - k.

Дальнейший анализ зависит от типа рассматриваемой модели. Для модели с фиксированными факторами ответ на основной вопрос дисперсионного анализа сводится к проверке гипотезы Н₀: M₁ = M₂ = … = M_k, то есть утверждения, что все групповые средние не зависят от влияния фактора А. Тогда, если верна Н₀, межгрупповая дисперсия должна быть равна внутригрупповой, то есть сформулированная гипотеза может быть заменена эквивалентной Н₀: s_m² = s_b². Допустим, что x_i - независимые наблюдения над случайной величиной X, распределенной нормально со средним  и дисперсией ². Тогда отношение (5.5) используется в качестве статистической характеристики критерия.

F(k, n-k) = . (5.5)

Если вычисленное значение F меньше табличного на 5-процентном уровне значимости , то гипотезу об отсутствии влияния фактора А не отклоняют. Если рассчитанное значение F больше табличного на 1- процентном уровне значимости, то различия по уровням фактора А являются существенными. Если же факторы случайны, то проверка гипотезы о равенстве групповых средних представляет небольшой интерес (уровни фактора А - сами случайные величины) и проверяют гипотезу о том, что межгрупповая дисперсия в генеральной совокупности равна нулю H_o: s_m² = 0.

Пример 5.3. Исследуется влияние средней высоты древостоя на величину среднего видового числа условно одновозрастных спелых ельников с помощью MS Excel (см. рис. 5.1). Числа наблюдений m_i и групповые средние M_i рассчитываются соответственно в колонках H и I. Число групп k = 8, общее число наблюдений N=40. Общее среднее M = 460 (ячейка I10). Квадраты отклонений вариант от групповых средних рассчитаны в ячейках B12…G19. В колонке J по формулам (5.1) - (5.5) вычислены показатели s₀²=36195, s_m²=14587, s_b² = 21608, учитывая, что число степеней свободы для групповой дисперсии равно k - 1 = 8 – 1 = 7, для общей N - 1 = 40 – 1 = 39, а для внутригрупповой N - k = 40 – 8 = 32. Статистическая характеристика из (5.5) F_ф = 2084/675 = 3,09. При  = 0,05 табличное значение F (из табл. 4.3 или с использованием функции MS Excel FРАСПОБР()) F_st(0,05;7;32) = 2,3. Так как F_ф > F_st, то гипотезу об отсутствии влияния высоты на среднее видовое число древостоя отклоняют: средние значения видовых чисел в генеральной совокупности не все равны между собой.

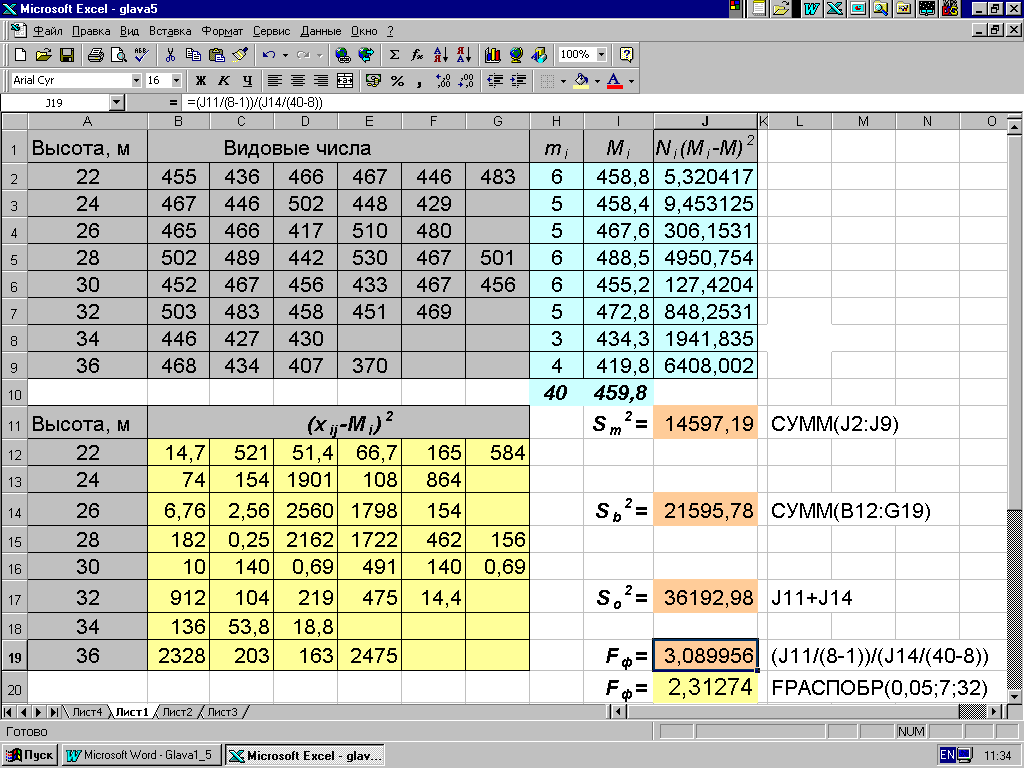
Рис. 5.1.