4.7. Использование пакетов прикладных программ
Ряд пакетов прикладных программ позволяют непосредственно проводить оценку статистических гипотез. К ним можно отнести:
Statistica;
SPSS;
Statgaphics;
MathCAD;
MS Exel.
Остановимся более подробно на последнем, т.к. он наиболее доступен в настоящее время для рядового пользователя. В состав Microsoft Excel входит набор средств анализа данных (называемый пакет анализа), предназначенный для решения сложных статистических и инженерных задач. Для проведения анализа данных с помощью этих инструментов следует указать входные данные и выбрать параметры; анализ будет проведен с помощью подходящей статистической или инженерной макрофункции, а результат будет помещен в выходной диапазон. Другие инструменты позволяют представить результаты анализа в графическом виде.
Двухвыборочный t-тест
Для вызова программы проведения t-теста необходимо выбрать команду «Анализ данных» в меню "Сервис". В списке "Инструменты анализа" (рис. 4.6) выбираем одну из строк
"Двухвыборочный t-тест с одинаковыми дисперсиями";
"Двухвыборочный t-тест с разными дисперсиями".
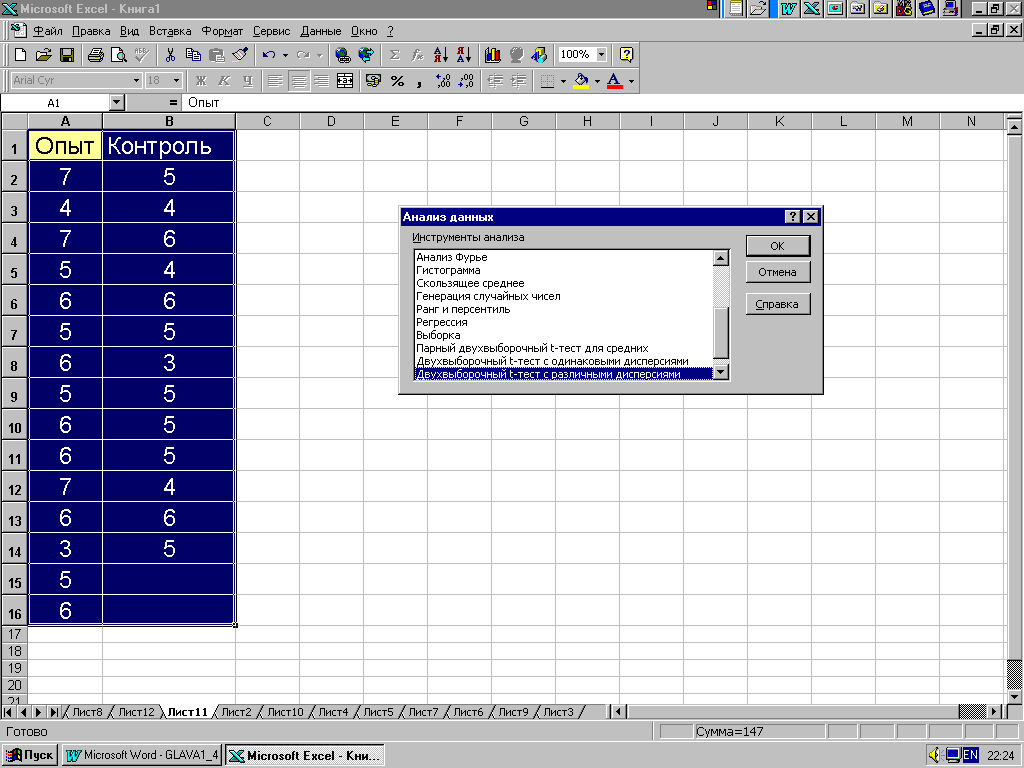
Рис. 4.6.
Для определенности рассмотрим решение в среде MS Excel задачи из примера 4.4 с применением процедуры "Двухвыборочный t-тест с разными дисперсиями". В появившемся диалоговом окне (рис. 4.7) последовательно вводим:
первый диапазон анализируемых данных, который состоит из столбца A2:A16;
второй диапазон анализируемых данных, который состоит из столбца В2:В14;
число, равное предполагаемой разности средних (0 указывает, что средние принимаются равными);
уровень надежности =0,05, который связан с вероятностью возникновения ошибки первого рода (опровержение верной гипотезы);
пометку, куда поместить результаты: на новый лист в текущей книге или на первый лист новой книги.
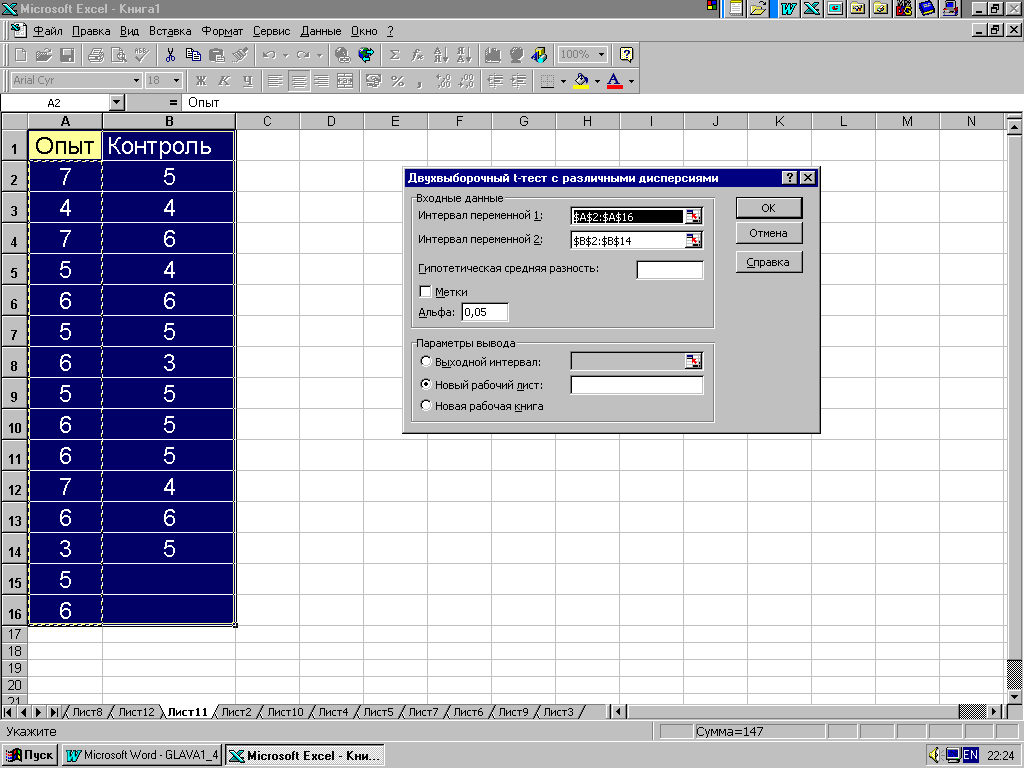
Рис. 4.7.
На рис. 4.8 приведены результаты расчета t-критерия tф=2,01, что соответствует результатам, полученным при решении примера 4.4 (см. рис. 4.3).
Двухвыборочный F-тест для дисперсий
Для вызова программы проведения t-теста необходимо выбрать команду "Анализ данных" в меню "Сервис". В списке "Инструменты анализа" (рис. 4.9) выбираем "Двухвыборочный F-тест для дисперсий". В появившемся диалоговом окне (рис. 4.10) последовательно вводим:
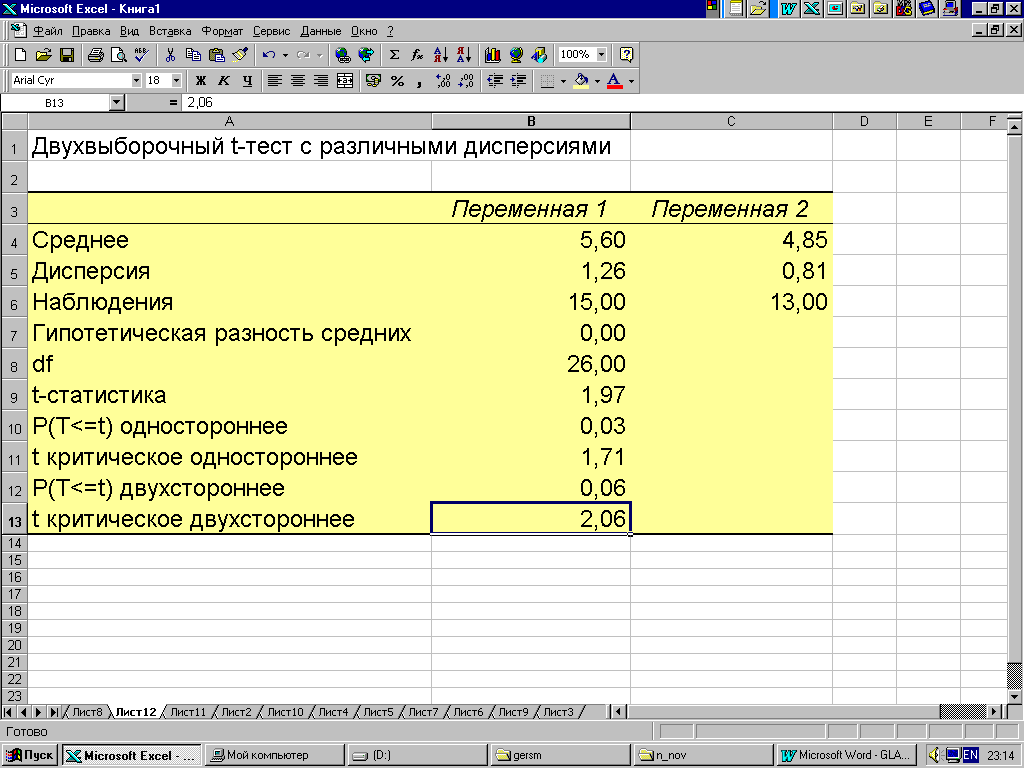
Рис. 4.8.
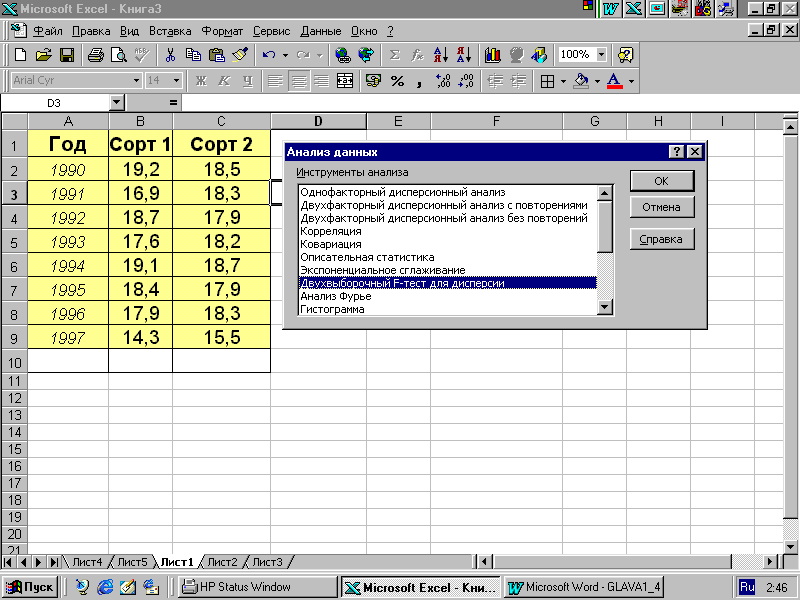
Рис. 4.9.
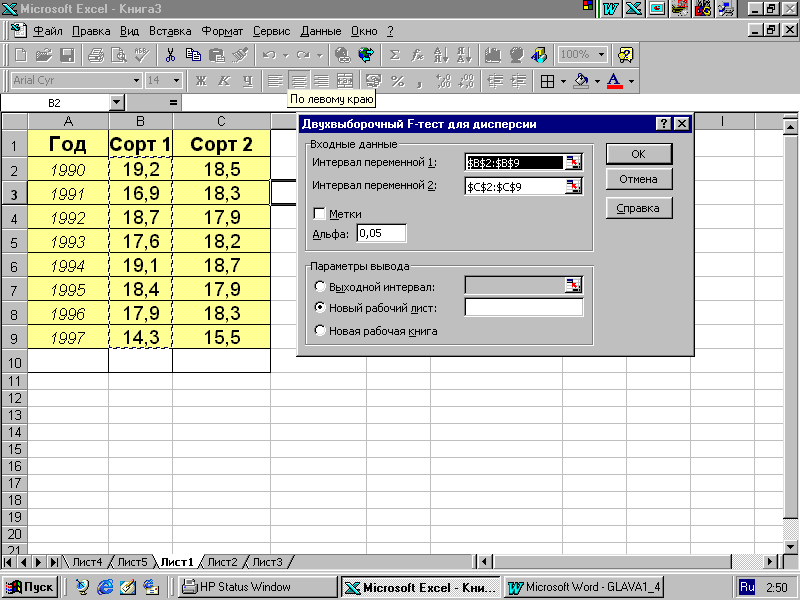
Рис. 4.10.
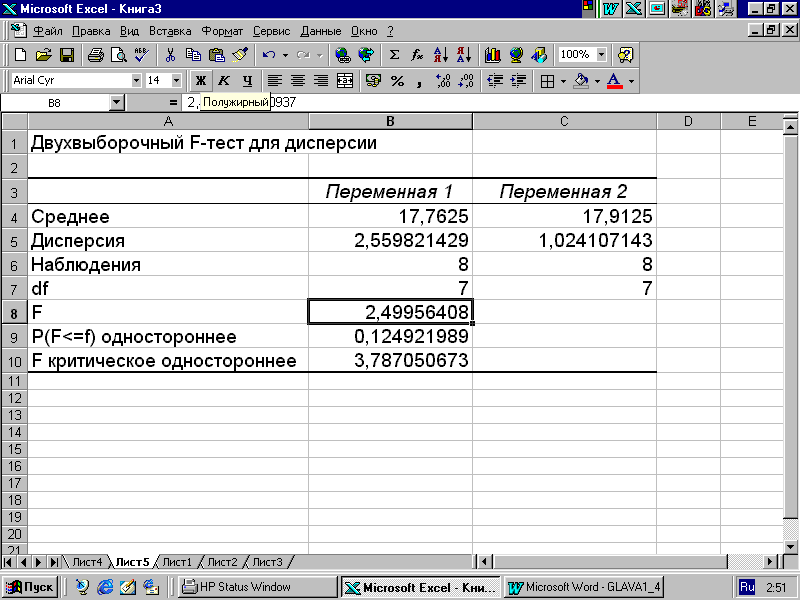
Рис. 4.11
первый диапазон анализируемых данных, который состоит из столбца B2:B9;
второй диапазон анализируемых данных, который состоит из столбца C2:C9;
уровень надежности =0,05, который связан с вероятностью возникновения ошибки первого рода (опровержение верной гипотезы);
пометку, куда поместить результаты: на новый лист в текущей книге или на первый лист новой книги.
Результаты расчета F-критерия для примера 4.6 (см. рис. 4.6) приведены на рис. 4.11.
Тест Хи-квадрат
Функция ХИ2ТЕСТ возвращает значение для распределения хи-квадрат (2). Критерий 2 используется для определения того, подтверждается ли гипотеза экспериментом.
Синтаксис:
ХИ2ТЕСТ(фактический интервал; ожидаемый интервал),
где
фактический интервал - это интервал данных, которые содержат наблюдения, подлежащие сравнению с ожидаемыми значениями;
ожидаемый интервал - это интервал данных, который содержит отношение произведений итогов по строкам и столбцам к общему итогу.
Критерий 2 сначала вычисляет 2 статистику, а затем суммирует разности между фактическими значениями и ожидаемыми значениями.
Пример
|
A |
B |
C |
1 |
Диаметр |
ni |
ni' |
2 |
8 |
11 |
12 |
3 |
12 |
118 |
120 |
4 |
16 |
181 |
167 |
5 |
20 |
124 |
131 |
6 |
24 |
67 |
71 |
7 |
28 |
31 |
34 |
8 |
32 |
17 |
14 |
9 |
36 |
9 |
9 |
ХИ2ТЕСТ(B3:B9;C3:C9) равняется 0,903. 2 статистика для вышеприведенных данных (7 степеней свободы) ХИ2ОБР(0,903;7) равняется 2,8, что соответствует полученному ранее результату (см. пример 4.3)