4.5. Сравнение дисперсий двух эмпирических совокупностей

(F-критерий)

Две выборочные совокупности, не различаясь значимо по своим средним значениям, могут различаться по стандартным отклонениям (или дисперсиям). Для проверки H₀-гипотезы о равенстве дисперсий нормально распределенных совокупностей, t-критерий оказывается недостаточно точным. В поисках лучшего критерия Р.Фишер предложил вместо выборочной разницы использовать разность между натуральными логарифмами этих величин, т.е. lns₁-lns₂ = z, где s₁s₂. Эта разность z распределяется нормально при наличии как больших, так и средних по объему статистических совокупностей. Д.Снедекор вместо логарифма отношений использовал отношения выборочных дисперсий, обозначив этот показатель в честь Фишера буквой F:

F = s₁²/s₂². (4.9)

Так как принято брать отношение большей дисперсии к меньшей, то F1. Чем значительнее неравенство между выборочными дисперсиями, тем больше будет и величина F, и, наоборот.

Величина F имеет непрерывную функцию распределения и зависит только от чисел степеней свободы k₁=n₁-1 и k₂=n₂-1. F полностью определяется выборочными дисперсиями и не зависит от генеральных совокупностей, т.к. предполагают, что они взяты из одной и той же генеральной совокупности (или из генеральных совокупностей с одинаковыми дисперсиями ₁² = ₂²). Функция распределения значений величины F при небольшом n имеет форму асимметричной кривой, которая по мере увеличения объема выборки (n) приближается к кривой нормального распределения.

Критические значения для F-критерия представлены в таблице приложения 6 для 5%-ного и 1%-ного уровней значимости и чисел степеней свободы k₁ и k₂. Если сравниваемые выборки извлечены из одной и той же генеральной совокупности (или из генеральных совокупностей с одинаковыми дисперсиями ₁² = ₂²), то величина F-критерия не превысит критические значения F_st. Если же выборки взяты из разных совокупностей (₁²  ₂²), а F_ф  F_st, то нулевая гипотеза должна быть отвергнута.

Пример 4.6. Два сорта условной растениеводческой продукции (рис. 4.5) имеют почти одинаковую среднюю урожайность M₁ = 17,8 ц/га; M₂ = 17,9 ц/га, но один из них (сорт 1) менее подвержен влиянию изменений погодных условий от года к году, чем другой сорт (s₁=2,56; s₂=1,02). В качестве критерия значимости различия дисперсии примем отношение их оценок (F-критерий).

В соответствии с обычными условиями применения F-критерия при вычислении величины F_ф надо всегда делить большую дисперсию на меньшую, соответственно изменив (при необходимости) обозначения. В рассматриваемом примере F_ф=2,5 при числах степеней свободы k₁=7 и k₂=7 (см. рис.4.5). В таблице (см. Приложения 6 и 7) находим, что при числе степеней свободы числителя k₁=7 и числе степеней свободы знаменателя k₂=7 критическое значение критерия Фишера F_st=3,79. Поскольку фактическое значение F_ф = 2,5 меньше 5%-ного критического значения F_st=3,79, то нулевая гипотеза не отвергается.

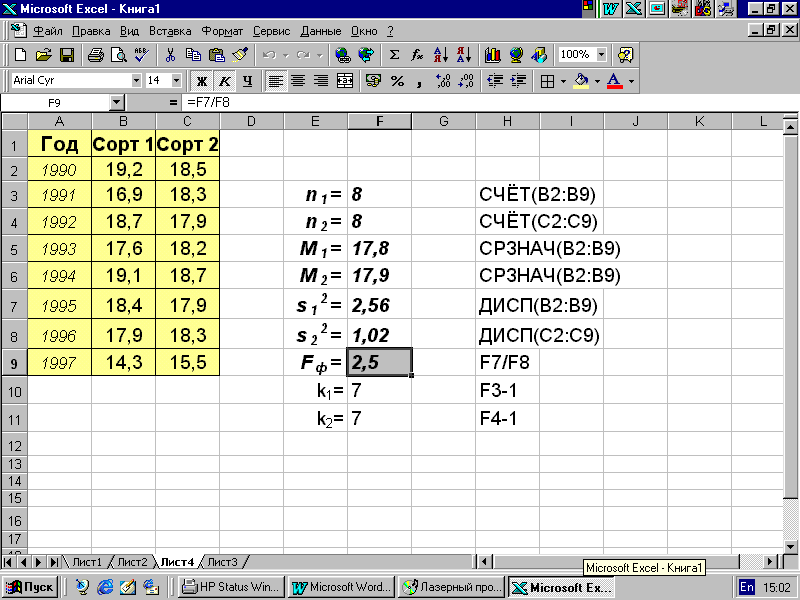
Рис. 4.5.