4.3. Сравнение эмпирического распределения с теоретическим (критерий "хи-квадрат")

При решении вопроса о различии между эмпирическим распределением и теоретическим нулевая гипотеза заключается в том, что генеральная совокупность, выборкой из которой является данное эмпирическое распределение, распределена по предполагаемому теоретическому закону, а отклонение эмпирического распределения от теоретического есть просто отклонение выборочного распределения от генерального (из-за случайного характера образования выборки).

Проверку гипотез о законах распределения производят с помощью специально разработанных критериев. Один из них - критерий согласия ² (предложен К.Пирсоном в 1890 г.) - нашел широкое применение в лесном хозяйстве. Критерий представляет собой сумму квадратов отклонений эмпирических частот n от теоретических n', отнесенную к теоретическим частотам:

. (4.2)

Распределение вероятных значений случайной величины ² является непрерывным и асимметричным. Оно зависит от числа степеней свободы k и приближается к нормальной кривой по мере увеличения числа испытаний N. Для того, чтобы оценки были более точными, выборка должна содержать не менее 50 вариант. Поэтому часто считают, что применение критерия ² требует того, чтобы в крайних классах вариационного ряда содержалось не менее пяти вариант. Если в крайних классах содержится меньше, чем пять вариант, то вычисленные и эмпирические частоты объединяются до указанного минимума и соответственно уменьшают число классов вариационного ряда. Число степеней свободы устанавливают по вторичному числу классов с учетом ограничений свободы вариации, которая бывает разной. Так, при оценке эмпирических распределений, следующих нормальному закону, число степеней свободы k=N-3 (с учетом трех ограничений вариации этого закона).

Для проверки нулевой гипотезы нужно фактически полученную величину _ф² сравнить с ее критическим значением _st². Если _ф²_st², то нулевая гипотеза должна быть отвергнута на принятом уровне значимости  с числом степеней свободы k. Значения теоретических критериев _st² приведены в Приложении 3.

Пример 4.3. Проверим гипотезу о согласии между теоретическим (логнормальная модель) и эмпирическими рядами распределения диаметра из табл. на рис. 4.2. Вычисленное в MS Excel значение _ф² = 2,78. Число степеней свободы k=8-3=5. Табличное значение критерия при k=5 при =0,1 равно ₀₁² = 15,09. Следовательно, вычисленная статистическая характеристика попадает в зону допустимых значений, и гипотеза о соответствии ряда распределения логнормальному закону не отвергается.

4.4. Сравнение средних значений двух эмпирических совокупностей (критерий Стьюдента)

Английский математик В. Госсет в 1908 г. нашел закон распределения величины

,

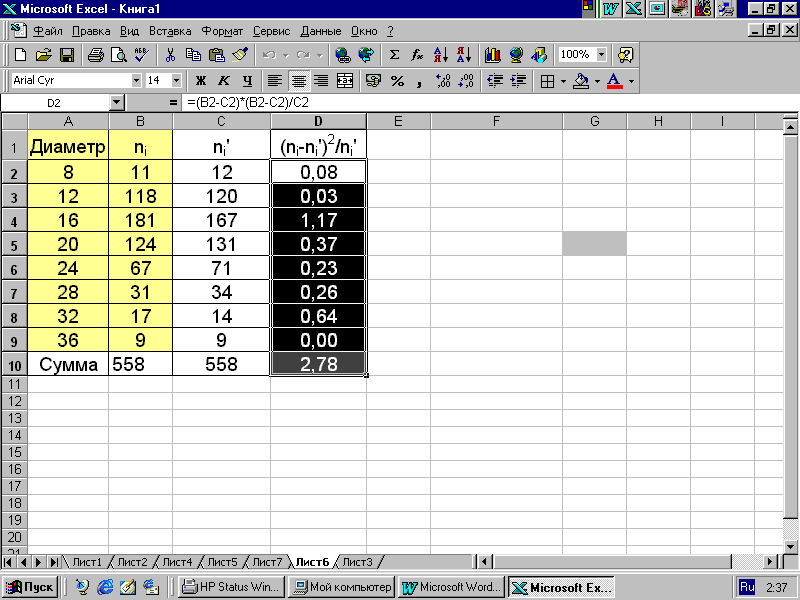
Рис. 4.2.

в которой генеральный параметр  заменен на его выборочную характеристику s, т.е. нашел закон распределения значений

. (4.3)

Оказалось, что отношение разности между выборочной и генеральной средними к ошибке выборочной средней непрерывно распределяется согласно следующей формуле:

для - < t< +, (4.4)

где

С - константа, зависящая только от числа степеней свободы;

k = n-1.

Из приведенной зависимости следует то, что t-распределение зависит только от объема выборки n, причем с увеличением n t-распределение быстро приближается к нормальному с параметрами =0 и =1 и уже при n30 не отличается от него.

Для практического использования t-распределения составлена специальная таблица, в которой содержатся критические значения t_st для разных уровней значимости  и чисел степеней свободы k ( Приложение 1). Сравнивая друг с другом две независимые выборки, взятые из нормально распределенных совокупностей с параметрами ₁ и _{2 ,} обозначим ₁ - ₂ = D, а дисперсию этой разницы ²_D. Значения генеральных параметров неизвестны, однако можно найти величины выборочных средних M₁, M₂, разность между ними M₁ - M₂ = d и ошибку разницы s_d. Ошибка разности средних s_d определяется по следующим формулам:

(4.5)

или

.

Так как, согласно H₀ - гипотезе ₁ - ₂ = 0, то t-критерий выражается в виде отношения разности выборочных средних к своей ошибке, т.е.

t = d / s_d . (4.6)

H₀ - гипотезу отвергают, если фактически установленная величина t-критерия t_ф превысит или окажется равной критическому значению t_st для принятого уровня значимости  и числа степеней свободы k = n₁+n₂-2, т.е. t_ф t_st .

Вышеизложенное применение t-критерия предполагает, что дисперсии сравниваемых групп одинаковы. Если это не так, то величину критерия и число степеней свободы находят по формулам:

, (4.7)

. (4.8)

Пример 4.4. Необходимо выяснить эффективность воздействия двухприемных постепенных рубок главного пользования на естественное лесовозобновление в сухих лишайниковых сосняках. Опыт может быть поставлен следующим образом: в качестве контроля закладывается делянка, на которой проводится сплошная рубка деревьев, в качестве опытного варианта служит двухприемная постепенная рубка. Площадки по учету возобновления одного размера размещаются в систематическом порядке вдоль делянок. При подсчете возобновления сосны получились результаты, приведенные на рис. 4.4, из которых следует, что средние значения для опытной и контрольной делянок не совпадают. Однако это еще не дает основания считать доказанной эффективность применения постепенных рубок в лишайниковых сосняках.

На рис. 4.3. приведена последовательность нахождения значений t-критерия t_ф = 2,01 и числа степеней свободы k=26 рассматриваемой задачи с использованием программы MS Excel. Так как t_ф < t₀₁ (26)  2,7 (см. Приложение 1), то нулевая гипотеза не отвергается. Следовательно, расхождение между опытом и контролем можно считать незначимым, т.е. применение постепенных рубок в сухих лишайниковых сосняках не обеспечивает увеличения естественного возобновления леса.

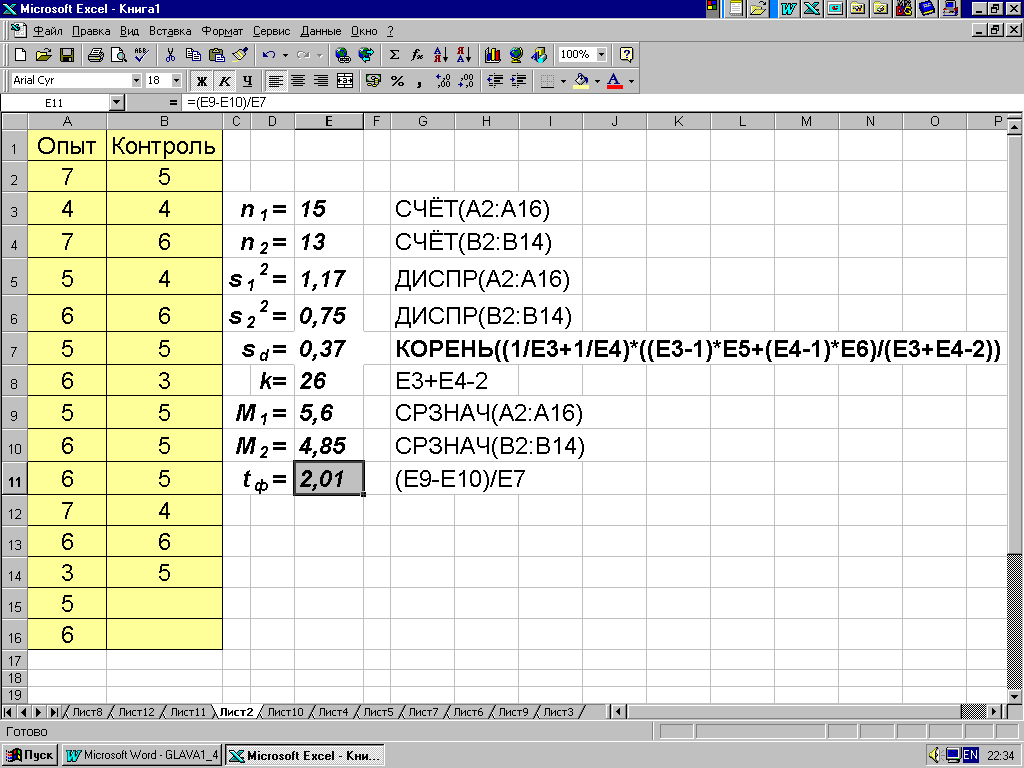
Рис. 4.3.

Пример 4.5. Каждый из двух сортов условной растениеводческой продукции высевался на семи делянках одного размера. На рис. 4.4 приведена урожайность в кг. Урожай сорта II на одной из делянок был поврежден и поэтому не включен в дальнейшую обработку. Там же приведена последовательность нахождения значений t-критерия рассматриваемой задачи с использованием программы MS Excel.

Так как средний урожай сорта I (M₁ = 8,27) выше, чем для сорта II (M₂ = 6,78), то напрашивается вывод, что вообще сорт I более урожайный. Но такой вывод может оказаться ложным, т.к. каждое из чисел 8,27 и 6,78 есть не генеральное, а выборочное среднее. Другая случайная выборка, также состоящая из 7 делянок, наверняка дала бы для M₁ значение, отличное от 8,27; в частности, это новое значение могло бы оказаться меньше, чем 8,27. С другой стороны, и для M₂ выборка дала бы значение, отличное от 6,78, в частности, могло бы получиться число большее, чем 6,78. Поэтому повторение всего опыта с обоими сортами могло бы дать результат M₁ < M₂. Очевидно, вероятность такого исхода тем меньше, чем больше отношение M₁ - M₂ к s_d.

Таким образом, опять приходим к критерию Стьюдента для оценки значимости того, что M₁ превышает M₂. Значение t-критерия t_ф = 3,15, а число степеней свободы k=11. Так как t_ф > t₀₁ (11)  2,17 (см. Приложение 1), то нулевая гипотеза отвергается.

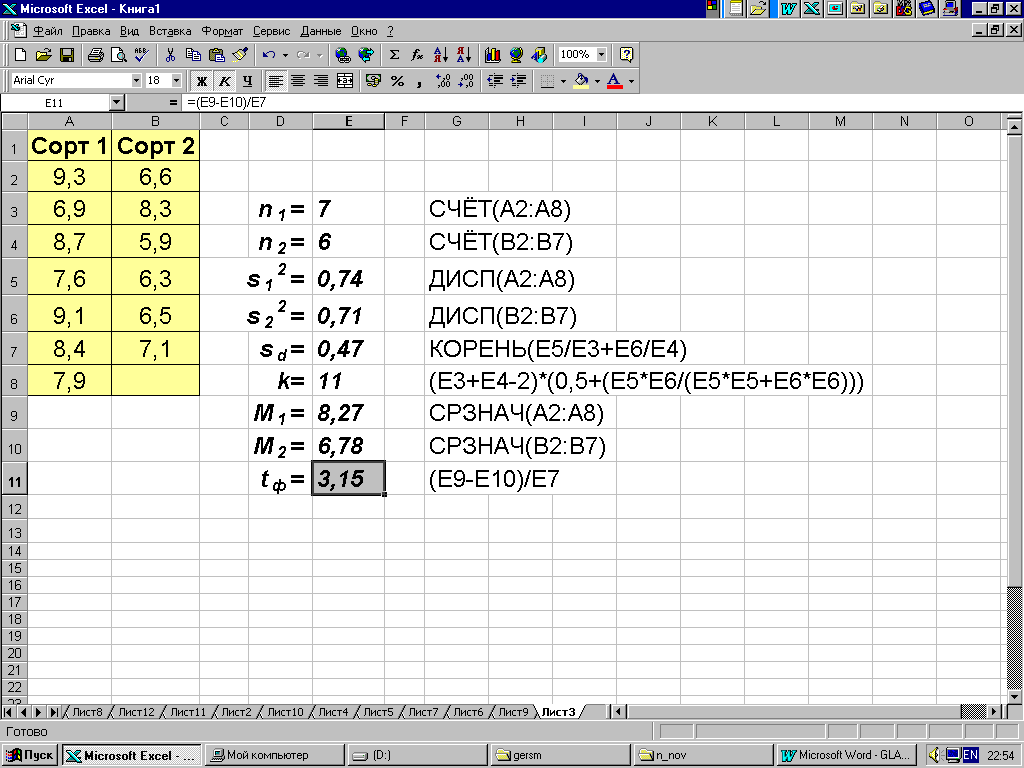
Рис. 4.4.