3.4.2. Бета-распределение

a>0, b>0, (3.13)

часто называют основным распределением для величин, ограниченных с двух сторон. Это удобная модель для многочисленных приложений, поскольку кривая бета- распределения может принимать самую различную форму в зависимости от величины параметров (рис. 3.5). Кроме того, посредством бета- распределения можно вычислять другие важные распределения. Если а>b>1 или b>a>1, то распределение одновершинное с максимумом в точке х=(а-l)/(a+b-2) с левосторонней асимметрией в первом и

правосторонней во втором случае; если а<1, b<1, то распределение имеет U-образную, а при а1, b<1 I-образную форму. При а<1, b1 кривая распределения убывающая. Если а=b, то распределение симметрично. В качестве примеров случайных величин, подчиняющихся бета - распределению, можно привести выработку бригады и др. за определенный

срок (смену, сутки), распределение большинства биометрических признаков деревьев и древостоев и др.

Рис. 3.5

Выражение

называют В- функцией или интегралом Эйлера II рода. Так как В- функция выражается через Г-функцию, то ее обычно вычисляют при ручном счете по таблице значений Г-функции ( Приложение 4).

Соотношения между параметрами бета - распределения и моментами, в частности средним и дисперсией, можно использовать для аппроксимации бета - распределения:

(3.14)

(3.15)

где

M - выборочное среднее;

s² - выборочная дисперсия.

Формула плотности (3.13) задает бета- распределение на интервале [0,1]. В конкретных задачах интервал обычно ограничен некоторыми значениями [x₁,x₂]. В этом случае плотность задается следующей формулой:

a>0, b>0. (3.16)

Пример 3.5. Аппроксимируем при помощи бета - распределения ряд распределения диаметра (рис. 3.6) в среде пакета MS Excel. Имеем x1=0,54 и x2=0,78 (начало и конец ряда), среднее M=0,6596 и дисперсию ²=3,7712. Замена x'=(x-0,54)/(0,78-0,54) дает M'=0,4983, величина разряда с=0,02/0,24=0,0833, дисперсия s'²=(cs)²=0,02619. Для нашего примера b=(0,5017/0,02619)(0,49830,5017-0,02619)= 4,2873, а a=(0,4983/0,5017)4,2873=4,2582. Умножив (3.13) на n/c и прологарифмировав полученное выражение, получим

lg(n_i)=3,6459+3,2582 lg(x’_i)+3,2873 lg(1-x’_i).

Схема вычисления n_i по последнему выражению приведена на рис. 3.6.

Ряд распределения диаметра можно аппроксимировать и при помощи встроенной функции бета- распределения БЕТАРАСП() по аналогии с примером 3.4.

Синтаксис:

БЕТАРАСП(x;альфа;бета;A;B),

где

X - это значение в интервале между A и B, для которого вычисляется функция.

Альфа - это параметр распределения.

Бета - это параметр распределения.

A - это необязательная нижняя граница интервала изменения x.

B - это необязательная верхняя граница интервала изменения x.

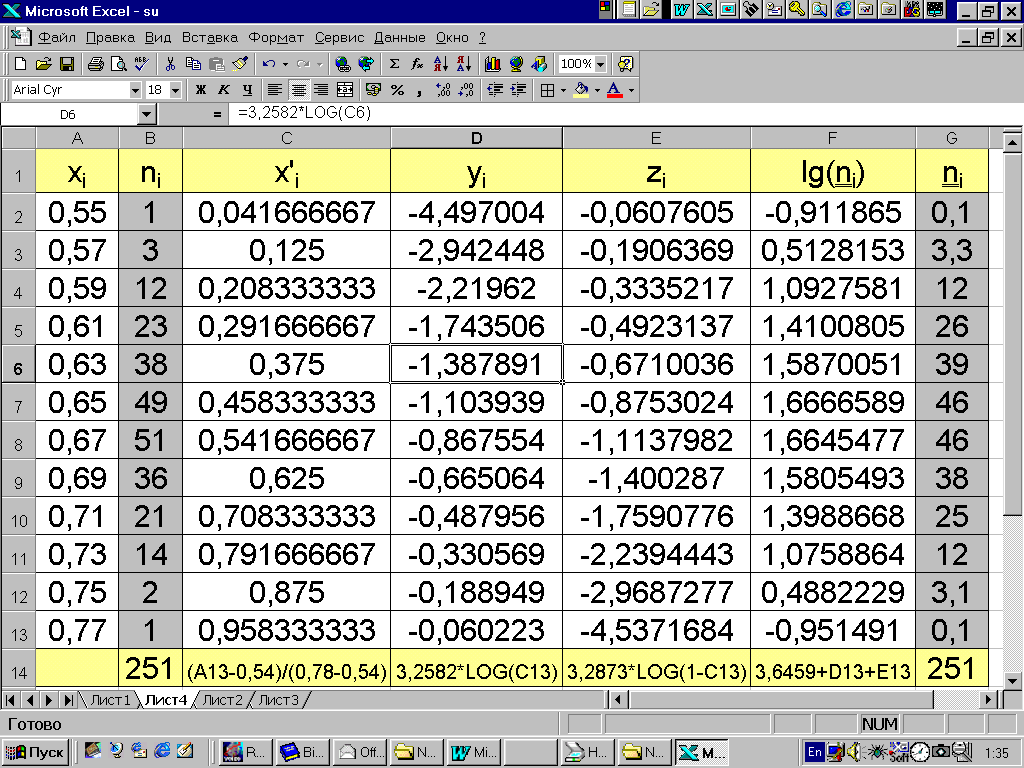
Рис. 3.6.

Основные типы дискретных распределений.

Обычно дискретные распределения применяют как модели подгонки. Все они так или иначе связаны с вероятностями появления событий по схеме Бернулли: при проведении серии из п независимых испытаний в каждом из них может произойти либо не произойти событие Л. Вероятность события остается на протяжении всех испытаний постоянной и равна р. Представляют интерес и встречаются в практических приложениях многочисленные задачи, связанные со схемой Бернулли.