3.3. Логнормальное распределение

Формируется в условиях, аналогичных предыдущему. Величина x распределена логнормально, если логарифмы ее значений u = lnx имеют нормальное распределение:

, (3.5)

где

u - среднее lnx;

_u - дисперсия lnx.

Распределение зависит от двух параметров (среднего и дисперсии логарифмов значений x), хотя можно ввести один или два параметра, ограничивающие размах распределения с одной или двух сторон.

Кривая распределения имеет правостороннюю асимметрию (рис. 3.2), которая возрастает с увеличением _u, поэтому хорошо аппроксимирует распределения с положительной косостью. Если для величины x известно среднее M и дисперсия ², то параметры логнормального распределения можно вычислить непосредственно по формулам:

_u² = ln(²/M² +1) , (3.6)

M_u = lnM - _u²/2 , (3.7)

а плотность логнормального распределения величины x

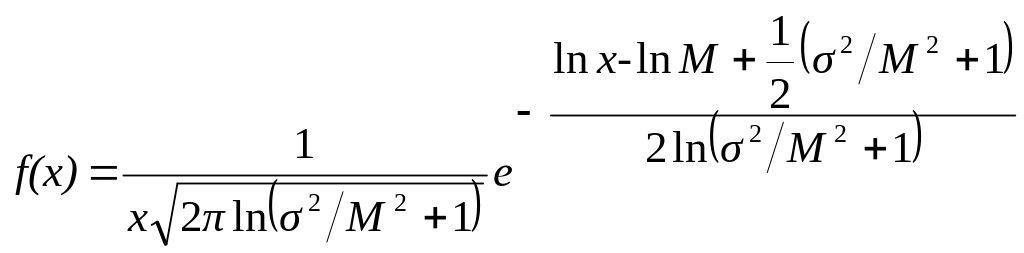. (3.8)

Уравнение (3.8) задано на интервале [0, ].

Имеются многочисленные примеры использования логнормального распределения как модели при свертке лесоводственной информации.

Пример 3.3. Вычислим выравнивающие частоты для ряда распределения диаметра табл. 2.1. Среднее значение и дисперсия этого ряда соответственно равны M=18,36 (см), ²=34,215 (см²), а =5,85 (см). По (3.6) и (3.7) находим о_u=0,311, M_u=2,862. Сравнение эмпирических и вычисленных частот свидетельствует о хорошем соответствии принятой модели ряду распределений (рис. 3.3).

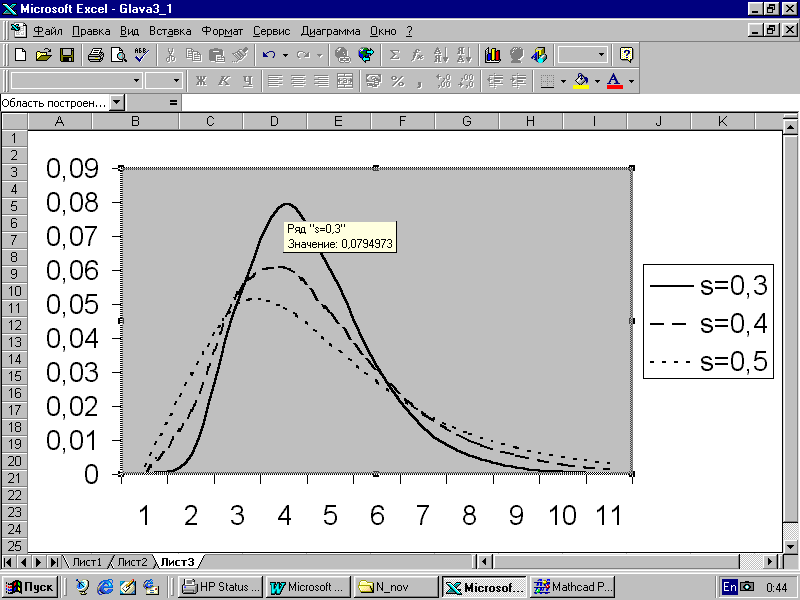
Рис. 3.2.

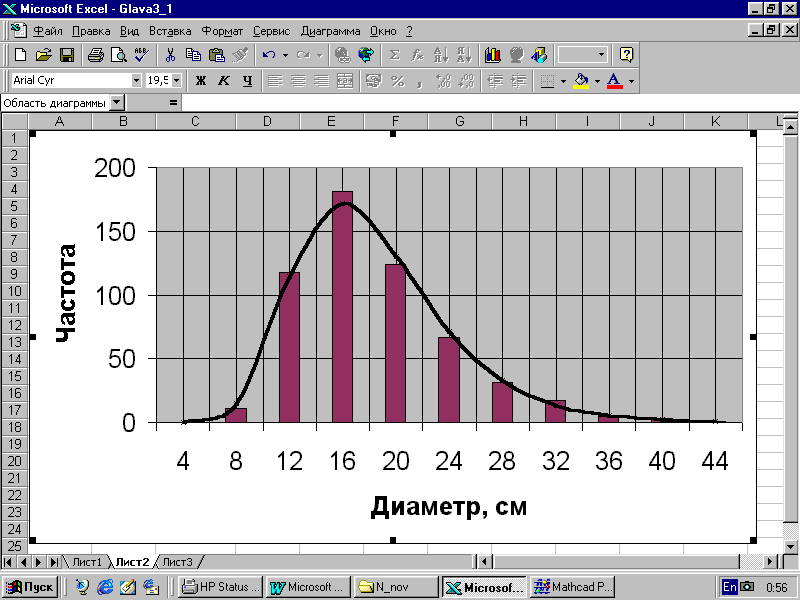
Рис. 3.3.

3.4. Гамма- и бета- распределения

Принадлежат к числу основных моделей, используемых при изучении распределений. Оба они связаны с одним из наиболее общих распределений - раcпределением Маркова, из которого можно получить практически все встречаемые в приложениях распределения как предельные стохастические кривые. Условия, при которых формируются гамма- и бета-распределения, весьма широки, в зависимости от величины входящих в них параметров. Как правило, они могут описывать любую практическую ситуацию из приведенных в настоящем параграфе, а ряд рассмотренных распределений может быть получен как частные случаи гамма- и бета- распределений.

3.4.1. Гамма-распределение - одна из основных статистических моделей для представления распределений случайных величин, ограниченных с одной стороны:

x0, a>0, b>0, (3.9)

где

b - параметр формы,

а - параметр масштаба,

Г(b) - интеграл Эйлера первого рода:

(3.10)

Форма и масштаб кривых распределения зависят от величины и соотношения параметров а и b. Если b1, то плотность гамма- распределения - убывающая кривая, если b>1, то распределение представлено одновершинной кривой с максимумом в точке (b-1)/а.

Для практического вычисления параметров а и b используют метод моментов, дающий приближенные, но, как правило, вполне приемлемые результаты. Cреднее значение гамма- распределения M=b/a, а дисперсия ²=b/a².

Вычислив на основании выборки значения M и s и приравнивая их соответствующим соотношением параметров, находим выборочные оценки а и b:

a = M/s² , (3.11)

b = a M. (3.12)

Пример 3.4. Аппроксимируем при помощи гамма- распределения ряд распределения диаметра (из табл. 2.1) в среде пакета MS Excel. Для нашего примера a=18.36/34.22=0.5365, а b=0.536518.36=9.85. Далее используем встроенную функцию ГАММАРАСП().

Синтаксис функции:

ГАММАРАСП(x;альфа;бета;интегральная),

где

x - значение, для которого требуется вычислить распределение;

aльфа - параметр распределения, соответствующий b в (3.9);

бета - параметр распределения, соответствующий 1/a в (3.9);

интегральная - это логическое значение, определяющее форму функции. Если интегральная имеет значение ИСТИНА, то функция ГАММАРАСП возвращает интегральную функцию распределения; если этот аргумент имеет значение ЛОЖЬ, то возвращается функция плотности распределения.

Сравнение эмпирических и вычисленных частот свидетельствует о неплохом соответствии принятой модели ряду распределений (рис. 3.4).

Рис. 3.4.