1) Свойства.

2) Применение.

3) Выражение через координаты сомножителей.

Проекция вектора на вектор:

Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.

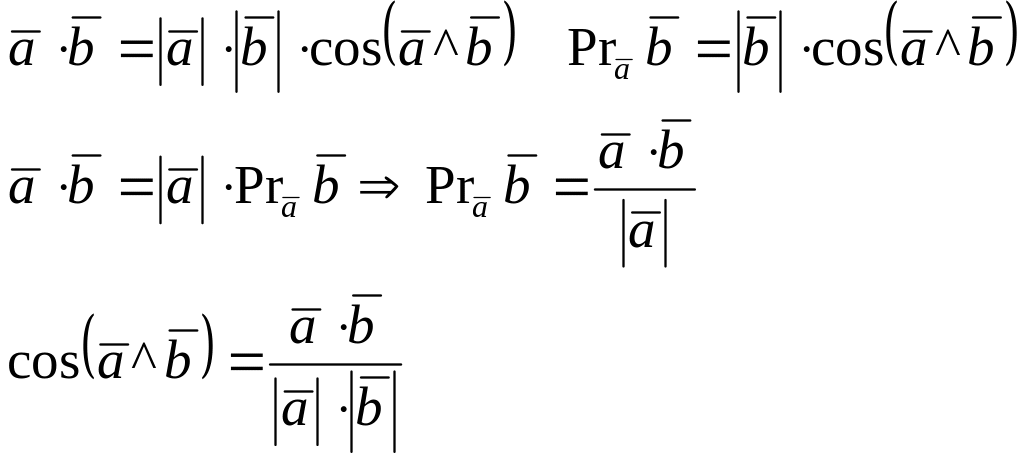
Свойства:

1. – Коммутативность.

2.

3.

4.

5.

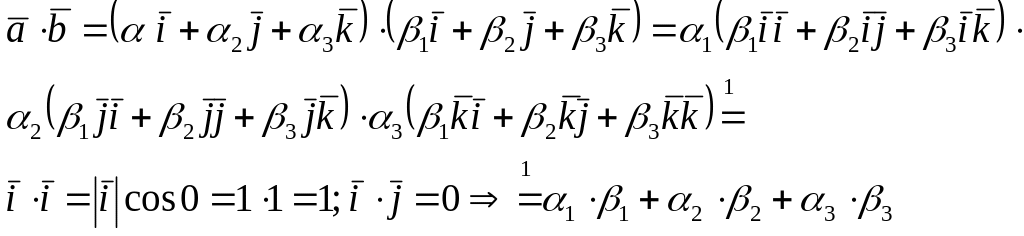
Скалярное произведение векторов, заданных своими декартовыми координатами равно сумме по парных произведений соответствующих координат сомножителей.

Применение скалярного произведения:

1. 

2. Определение перпендикулярности векторов, как скалярное произведение, равное нулю.

3. 

4. 

Вопрос № 19: Векторное произведение векторов:

1. Векторное произведение векторов.

1) Свойства.

2) Геометрический смысл.

3) Выражение через координаты сомножителей.

Векторным произведением векторов называется вектор, обозначаемый , который обладает двумя свойствами:

1. Перпендикулярен двум исходным векторам.

2. Составляет с исходными векторами правую тройку

3. 

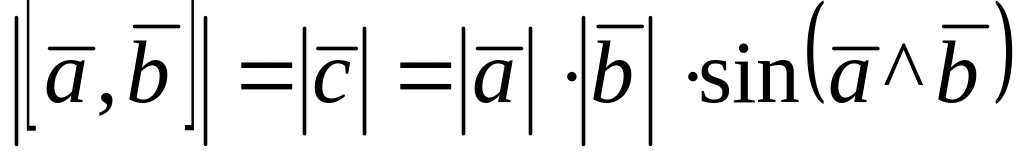
Направление результирующего вектора определяется по правилу буравчика.

Свойства векторного произведения:

1. – проверка на колиниарности.

2. 

3. 

4. 

5. 

6. 

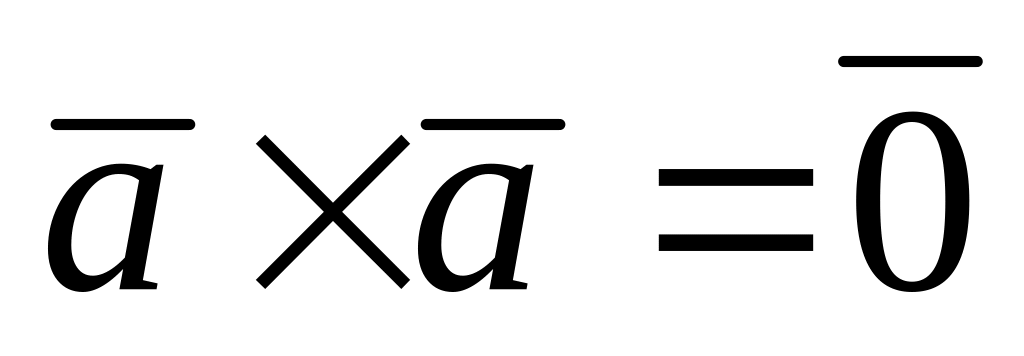
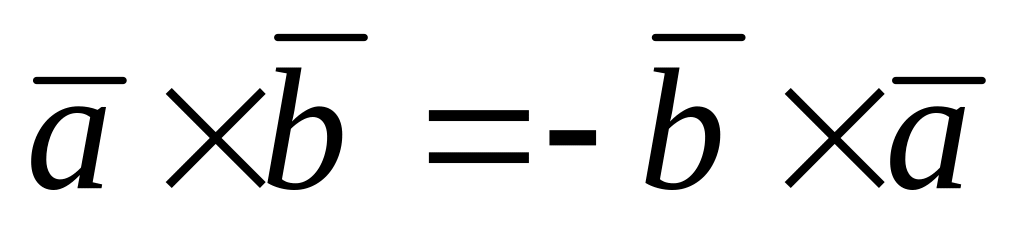
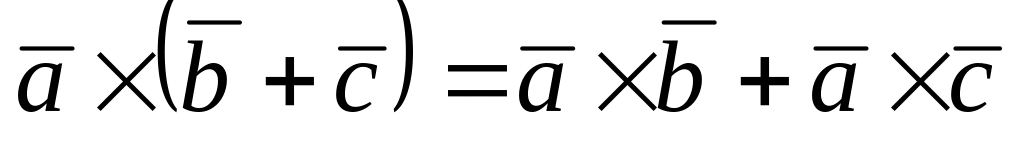
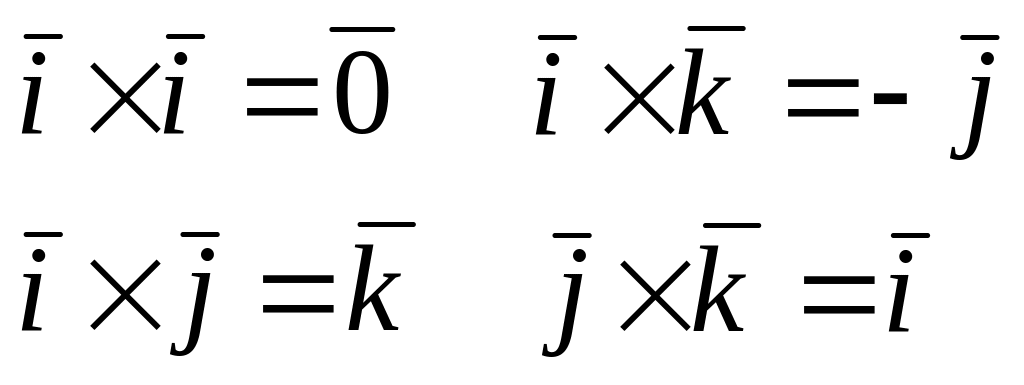
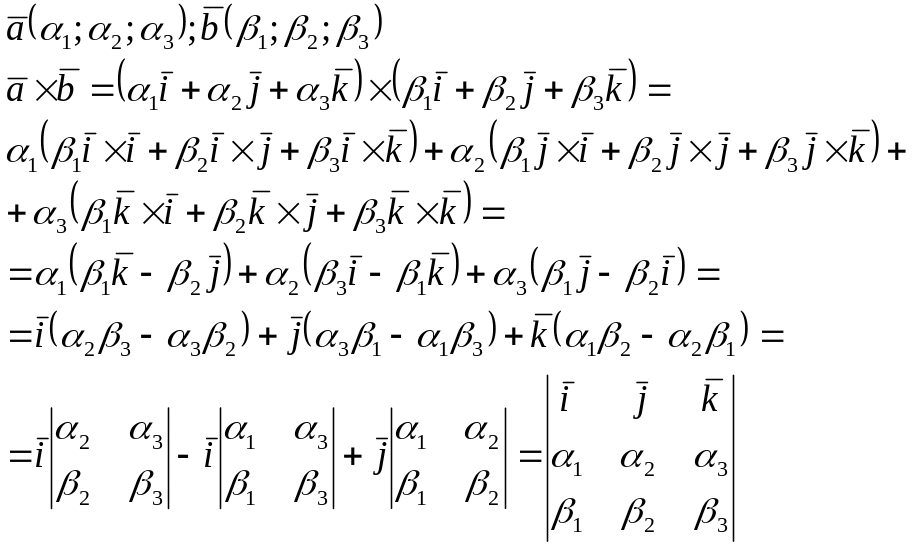
Вопрос № 20: Смешанное произведение векторов:

1. Смешанное произведение векторов.

1) Свойства.

2) Геометрический смысл.

3) Выражение через координаты сомножителей.

Смешанным произведением трёх векторов называется число, обозначаемое , равное скалярному произведению трёх его сомножителей, на векторное произведение двух первых.

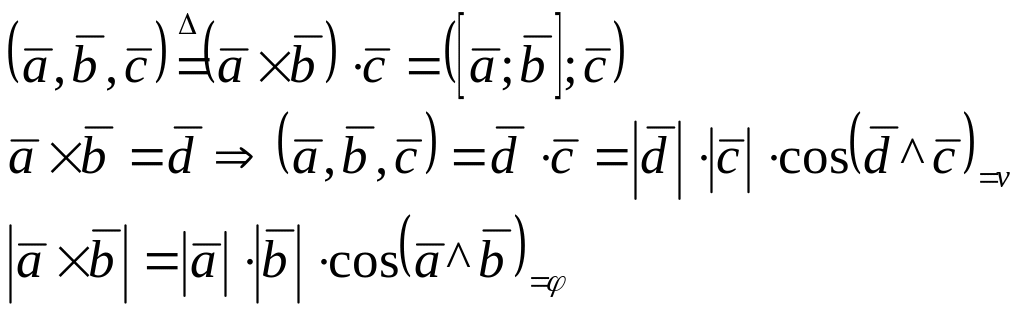
1. 0, когда , а значит угол v – острый, следовательно, вектора составляют правую тройку.

2. 0, когда , а значит угол v – тупой, следовательно, вектора составляют левую тройку.

3.

Свойства смешанного произведения:

1. =0 тогда, когда комплонарны.

2.

3.

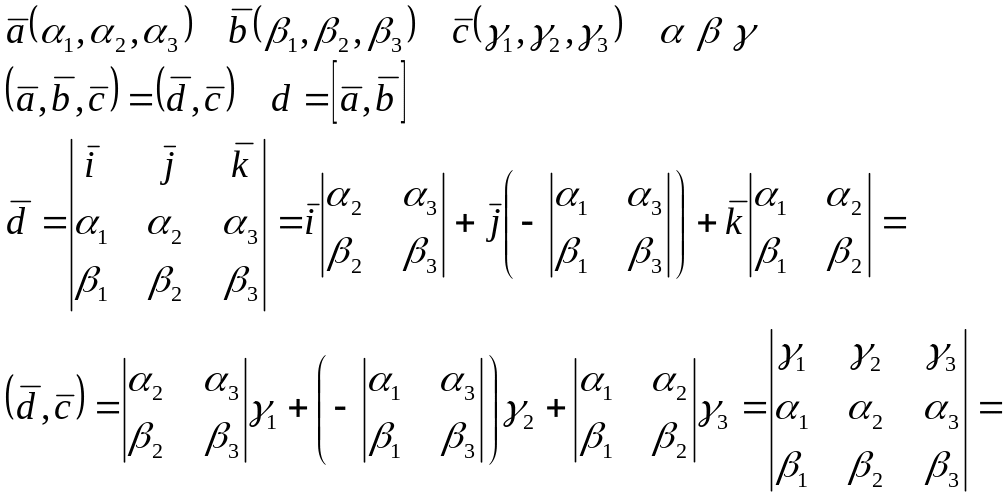
Вопрос № 21: Прямая на плоскости:

1. Прямая на плоскости.

1) Уравнения.

1) Общее.

2) Параметрическое.

3) Каноническое.

2) Расстояние до точки.

3) Угол между прямыми.

На плоскости задана прямоугольная декартова система координат.

Уравнение называется уравнением линии L на плоскости, если координаты всех точек линии подчиняются закону F, а координаты всех точек, не лежащих на линии .

Линия – это геометрическое место точек, координаты которых удовлетворяют закону – основное уравнение прямой на плоскости.

Векторное уравнение прямой на плоскости:

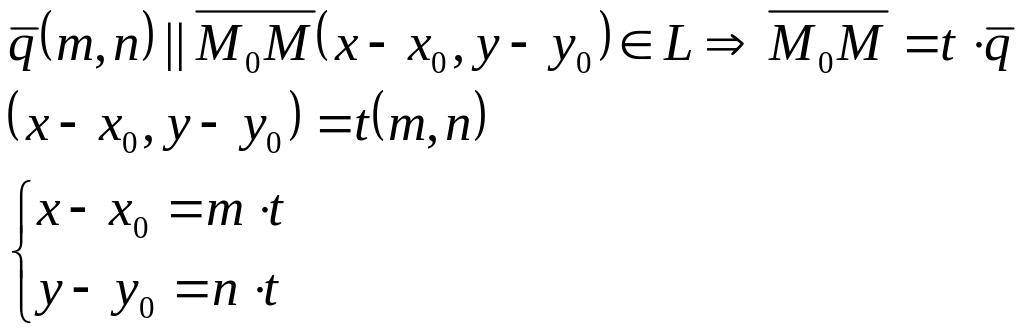
Параметрическое уравнение прямой на плоскости:

Каноническое уравнение прямой на плоскости:

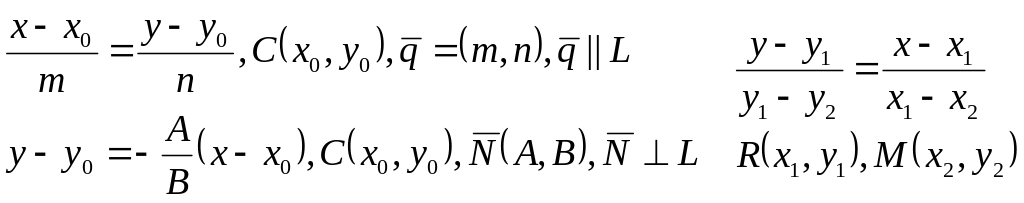
Расстояние от точки до прямой:

Угол между прямыми:

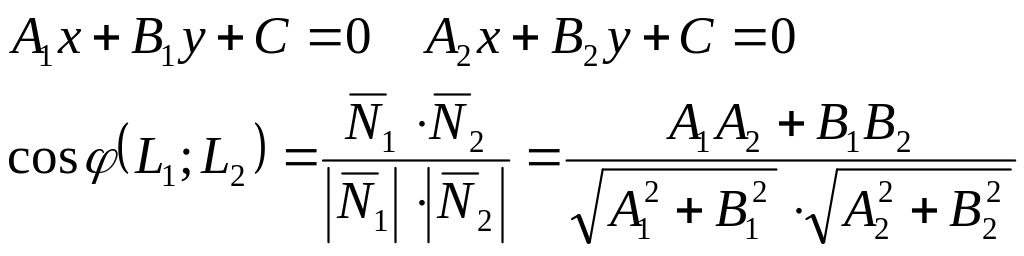
Вопрос № 22: Плоскость в пространстве:

1. Плоскость в пространстве.

1) Уравнение:

1) Общее.

2) Параметрическое.

3) Каноническое.

2) Расстояние до точки.

3) Угол между плоскостями.

Общее уравнение плоскости в пространстве:

Параметрическое уравнение прямой:

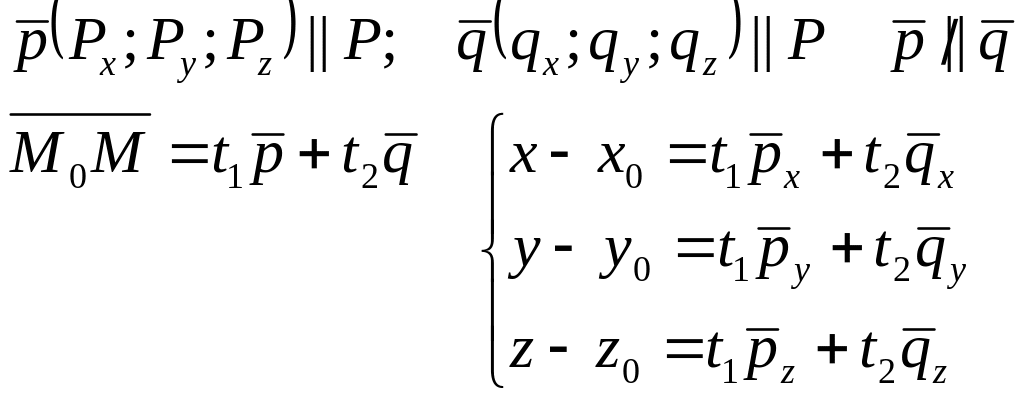
Векторное уравнение плоскости в пространстве:

Расстояние от точки до плоскости:

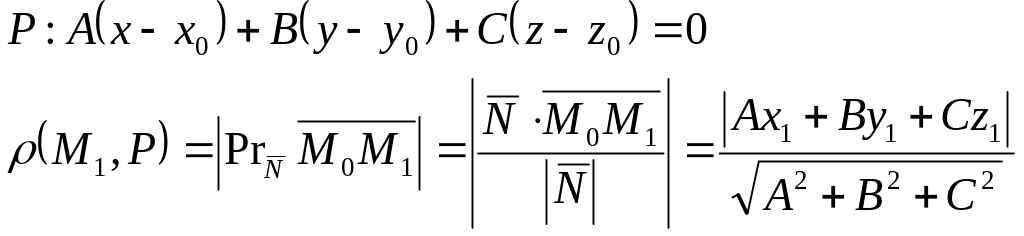
Уравнение плоскости, проходящей через три заданные точки:

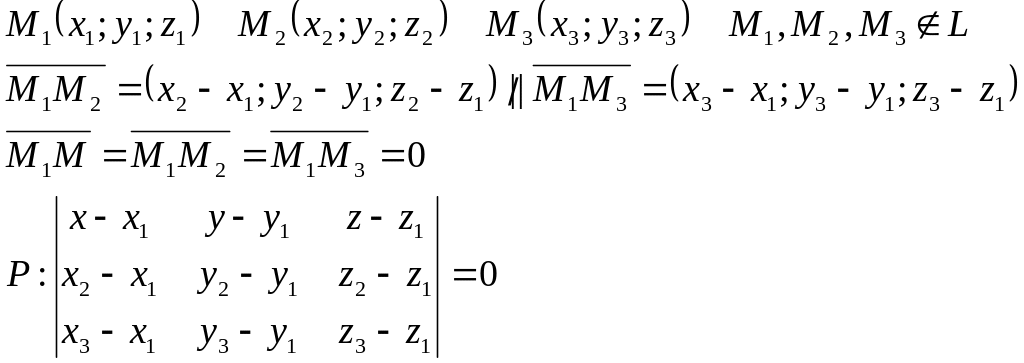
Угол между прямой и плоскостью:

Углом между прямой и плоскостью называется любой смежный угол, образованный самой прямой и проекцией этой прямой на плоскости:

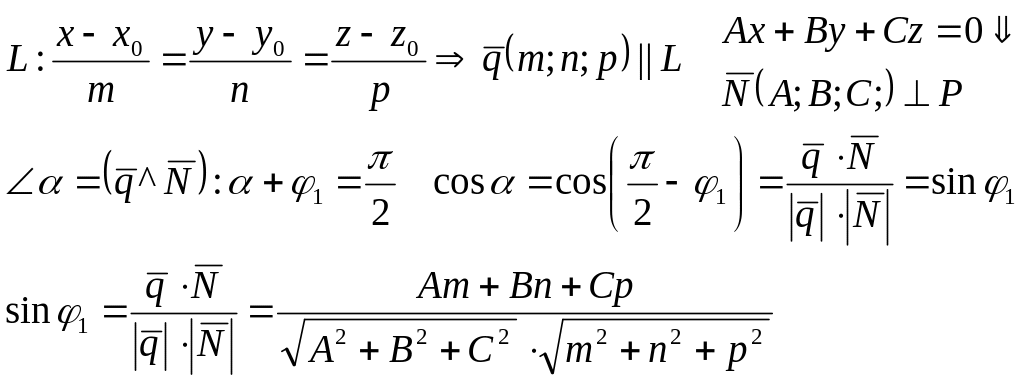
Вопрос № 23: Прямая в пространстве:

1. Прямая в пространстве.

1) Уравнение.

1) Общее.

2) Параметрическое.

3) Каноническое.

4) Переходы между ними.

2) Угол между прямыми.

3) Угол между прямой и плоскостью.

Общее уравнение прямой в пространстве:

Общее уравнение прямой в пространстве выводится из условия задания прямой, как пересечения двух плоскостей:

Параметрическое уравнение прямой:

Каноническое уравнение прямой:

Угол между прямыми:

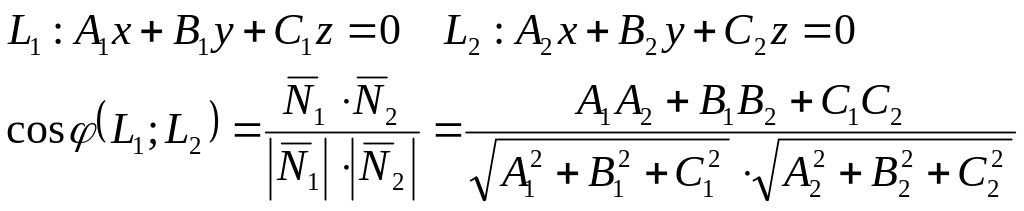
Угол между прямой и плоскостью:

Вопрос № 24: Три типа взаимного расположения прямых в пространстве:

1. Три типа расположения двух прямых в пространстве:

1) Параллельные прямые.

2) Пересекающиеся.

3) Скрещивающиеся прямые.

2. Расстояния:

1) Между точкой и прямой.

2) Между параллельными прямыми в пространстве.

3) Между скрещивающимися прямыми в пространстве.

Параллельные прямые в пространстве:

Пересекающиеся прямые в пространстве:

Скрещивающиеся прямые:

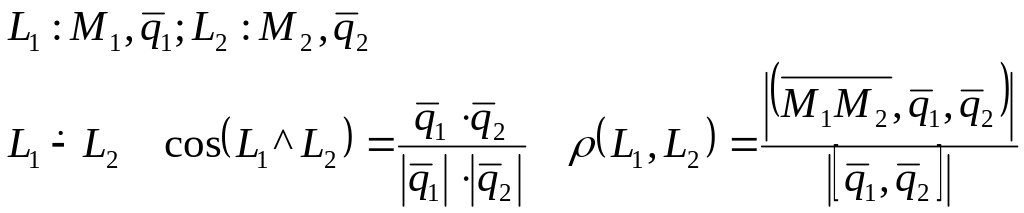
Вопрос № 25: Кривые второго порядка:

1. Кривые второго порядка.

1) Типы.

1) Геометрические определения

2) Канонические уравнения.

2. Общее уравнение.

1) Преобразование к каноническому.

1) Перенос начала координат.

2) Поворот осей.

Кривой второго порядка называется алгебраическая линия второй степени, общее уравнение которой имеет следующий вид: . Любые уравнения такого вида можно привести к каноническому виду.

Кривые второго порядка подразделяются на Эллипс, Гиперболу и Параболу.

Эллипс:

Эллипсом называется геометрическое место точек плоскости, сумма расстояний каждой из которых до двух заданных фокусов есть величина постоянная

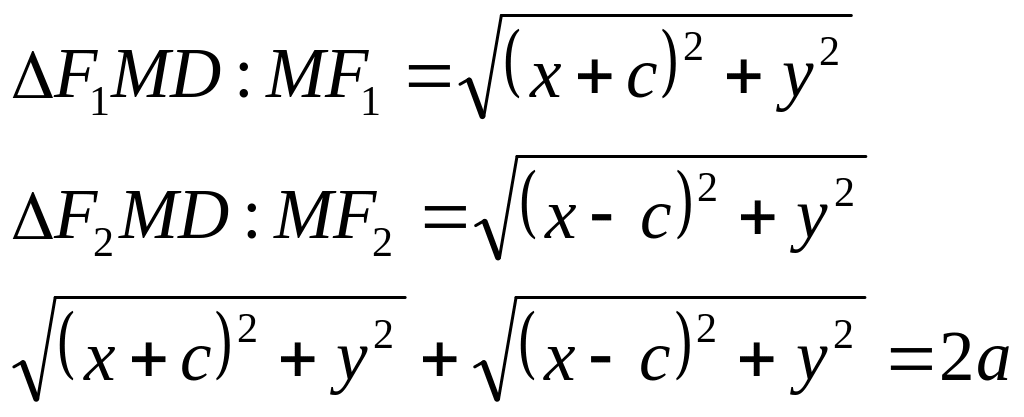
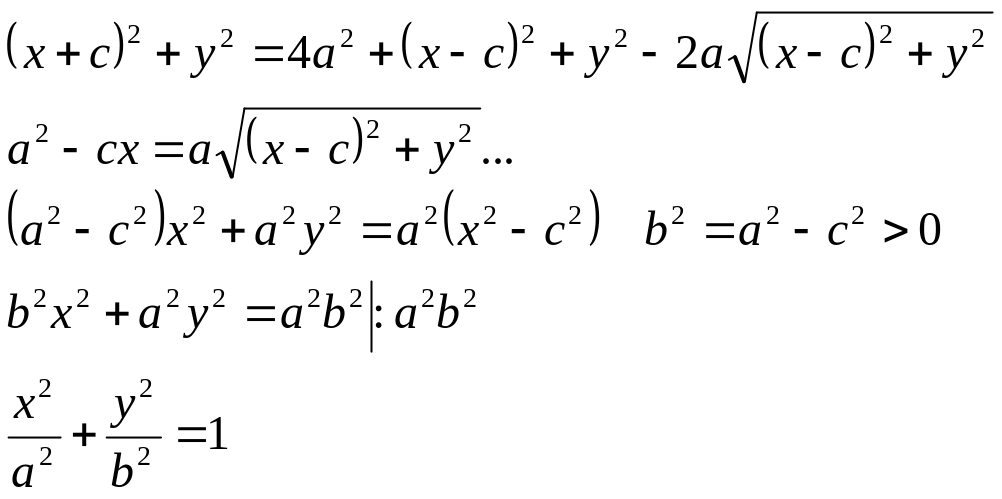
Эксцентриситет:

Эксцентриситет характеризует степень сжатия

Коэффициент сжатия:

Параметрическое уравнение эллипса:

Оптические свойства:

Если взять эллиптическое зеркало, и в один из фокусов поместить источник света, то отражённые лучи пересекутся в другом фокусе.

Гипербола:

Гиперболой называется геометрическое место точек плоскости, абсолютная величина разности расстояний каждой из которых до двух заданных фокусов, находящихся на расстоянии 2с является величиной постоянной, равной 2а.

Эксцентриситет:

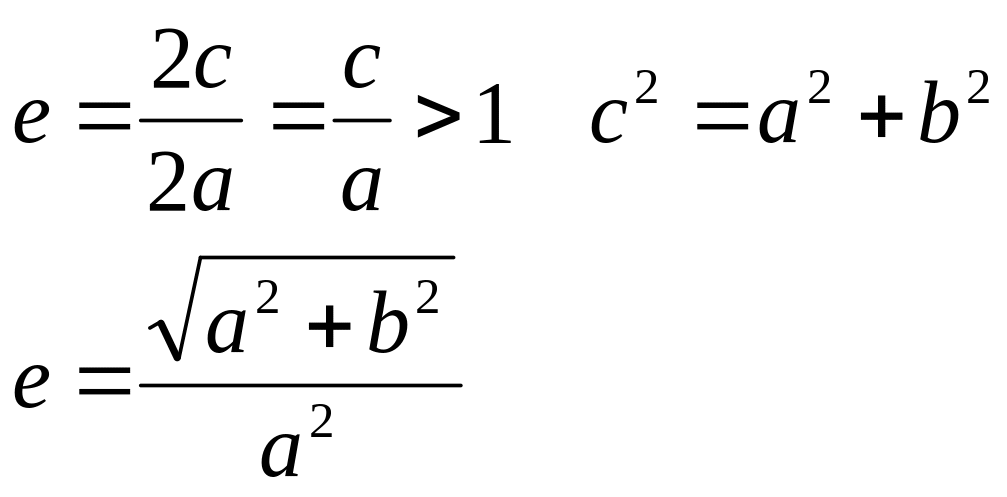
Оптические свойства:

Гиперболическое зеркало даёт расходящийся пучок света.

Парабола:

Параболой называется геометрическое место точек плоскости, каждая из которых равноудалена от заданной точки – фокуса, и заданной прямой, называемой директрисой, причём расстояние от точки до прямой равно р:

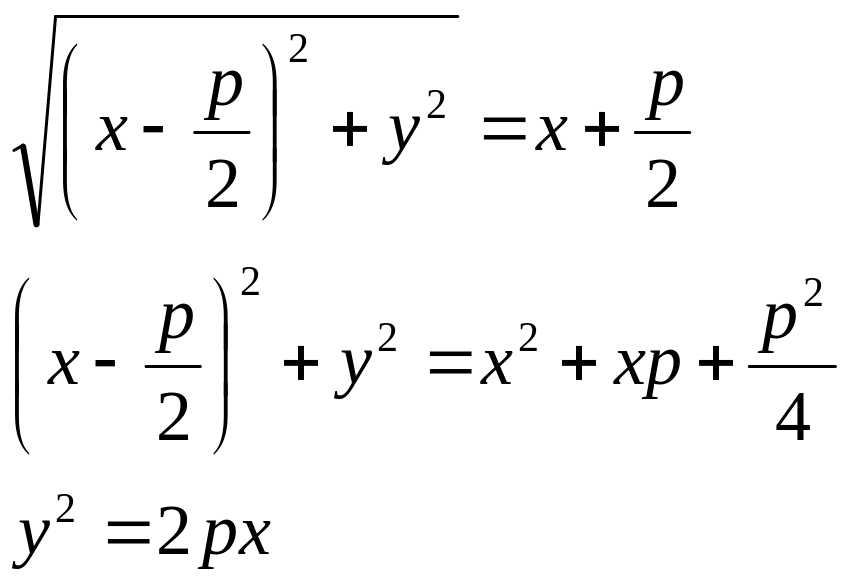
Приведение кривой к каноническому виду:

Приведение общего уравнения второго порядка к каноническому виду производится в два действия:

1. Определение новой системы координат, оси которой повёрнуты относительно основной. Поворот определяется слагаемыми, представляющими собой произведение переменных.

2. Сдвиг начала координат вдоль осей новой системы. Сдвиг определяется линейными членами уравнения. Преобразование на данной стадии осуществляется выделением полных квадратов.

– квадратичная форма.

Приведение квадратичной формы к взвешенной сумме квадратов: !!!¿¿¿

Вопрос № 26: Поверхности второго порядка:

1. Поверхности второго порядка.

1) Эллипсоид.

2) Конус.

3) Гиперболоиды.

2. Канонические уравнения.

3. Исследование форм методом сечений.

С помощью поворота можно исключить смежные произведения переменных, каждая их которых определяет свою поверхность (эллипсоид, гиперболоид, параболоид, конус, цилиндроид).

Исследование функции поверхности проводится при помощи канонического уравнения с помощью метода сечений.

Если все переменные в уравнении есть и все входят квадратично, то:

1. Если все слагаемые положительны, то – Эллипсоид.

1) Строим координаты сечения х=0 (плоскость по YZ)

2)

3)

2. – Однополосный гиперболоид.

1) Гипербола:

2) Эллипс:

3) Парабола:

3. – двух полосный гиперболоид:

1) Гипербола:

2) Гипербола:

3) Эллипс:

4. – Эллиптический конус

1) Пересекающиеся прямые:

2) Эллипс:

3) Пересекающиеся прямые:

Вопрос № 27: Поверхности второго порядка:

1. Поверхности второго порядка

1) Параболоиды.

2) Цилиндроиды.

2. Канонические уравнения.

3. Исследование форм методом сечений.

Все переменные есть, но две из них входят с квадратами, а одна линейно, получаемые таким образом поверхности называются параболоидами.

1. – эллиптический параболоид.

1) – Парабола.

2) – Парабола.

3) – Эллипс.

2. – Гиперболический параболоид.

1) – Парабола, ветви вверх.

2) – Парабола, ветви вниз.

3) – Гипербола, симметрия относительно ОХ

Цилиндроиды:

Отсутствует одна из переменных:

3. – Эллиптический цилиндр.

1) – две параллельные прямые.

2) – две параллельные прямые.

3) – Эллипс.

4.

1) – две параллельные прямые.

2) – две параллельные прямые.

3) – Гипербола.

5. – Параболический цилиндр.

Вопрос № 28: Квадратичная форма многих переменных и её матрица:

1. Квадратичная форма многих переменных.

1) Её матрицы.

2. Приведение квадратичной формы к каноническому виду.

1) Приведение квадратичной формы к взвешенной сумме квадратов.

Квадратичной формой N переменных называется однородный многочлен второй степени относительно этих переменных:

Квадратичную форму всегда можно представить в матричном виде:

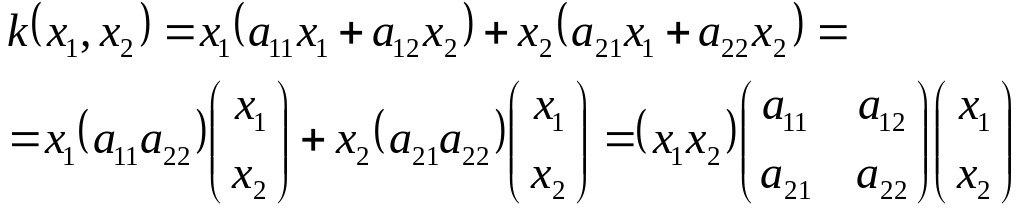
Диагональным, или каноническим видом квадратичной формы называют её вид в случае, если матрица коэффициентов является диагональной:

Для выполнения преобразования необходимо установить связь между исходными и новыми переменными

Линейное преобразование одной группы переменных: такое преобразование, при котором каждая из переменных х – линейная комбинация переменной у:

Если С не вырождена, то есть её определитель не равен нулю, существует обратная к ней матрица, такая, что:

Для приведения квадратичной формы к каноническому виду необходимо произвести такие преобразования, что бы матрица квадратичной формы стала диагональной.

Условия приведения квадратной матрицы к диагональному виду:

Если квадратная матрицы порядка п имеет несколько линейно независимых собственных векторов и соответствующих собственных значений, то она может быть приведена к диагональному виду, причём элементы диагональной матрицы являются собственные значения.

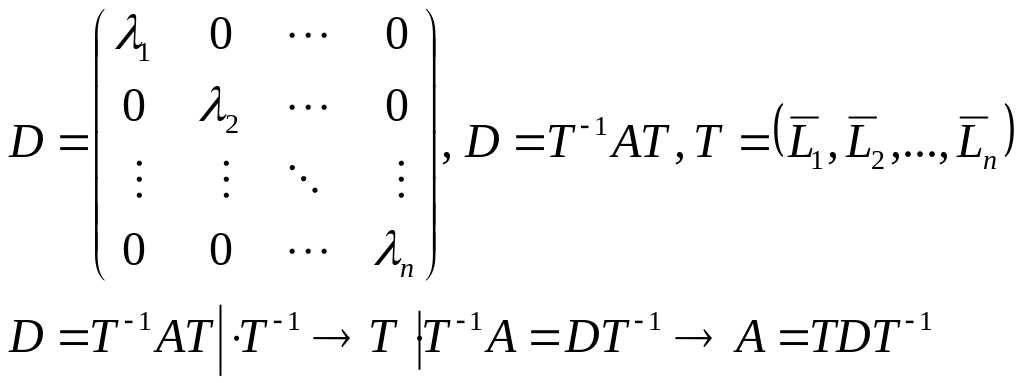
Пример:

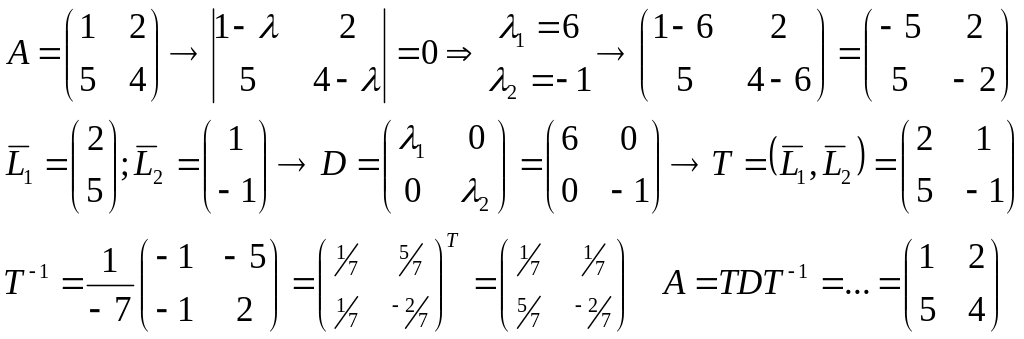
Понятие об ортогонально матрице:

Для того, что бы новая, повёрнутая система координат была прямоугольной необходимо, что бы матрицы линейных преобразований была ортогональной.

Матрица линейных преобразований называется ортогональной, если её столбцы являются ортогональными арифметическими векторами.

Арифметическим вектором в линейной алгебре называется столбец из нескольких чисел

Скалярным произведением двух векторов одной и той же размерности назы­вается сумма по парных произведений соответствующих координат.

Нормой вектора называется квадратный корень из его скалярного квадрата.

Матрица С называется ортогональной, если её столбцы нормированы.

Ортогональная матрица обладает следующим свойством: операцию обращения можно заменить операцией транспонирования.

Процедура Шмидта ортогонализации матриц:

Любую систему линейно независимых векторов, то есть базис п-мерного пространства, можно преобразовать в ортогональную систему векторов с помощью следующей рекуррентной процедуры:

Любая арифметическая система координат может быть преобразована в прямоугольную систему координат:

Доказательство:

Применяя Процедуру Шмидта к столбцам невырожденной матрицы С можно сделать её ортогональной:

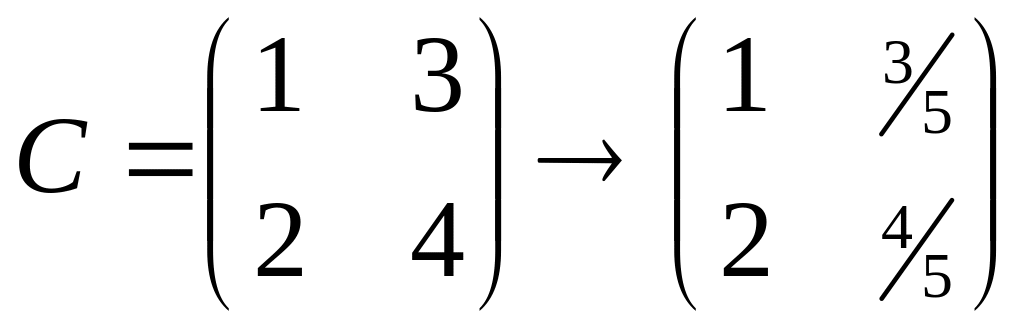
Приведение квадратичной формы к каноническому виду:

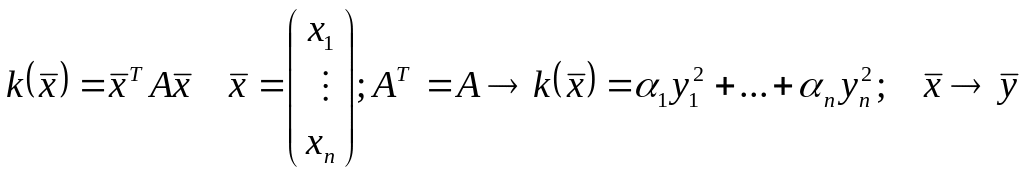
Для этого воспользуемся свойством собственных векторов и собственных значений матрицы А. Так как матрица А симметрична, все её собственные значения, среди которых могут быть кратные, являются действительными числами.

Каждому кратности соответствует штук собственных векторов (линейно независимых). Следовательно, полная система собственных векторов матрицы А состоит из п штук, и все они линейно независимы, по этому матрицу из квадратичной формы может быть преобразована к диагональному виду:

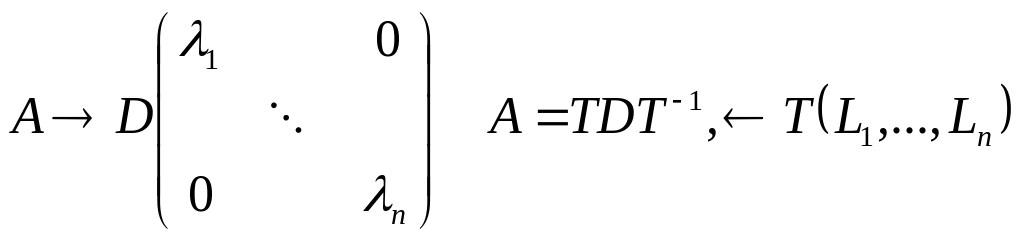
Так как все столбцы линейно независимой матрицы Т можно сделать ортогональными с помощью процедуры Шмидта, и нормированными, то:

В результате матрицу квадратичной формы можно представить в виде: , тогда подставив это выражение в формулу квадратичной формы, получим:

Замена

Любую квадратичную форму можно преобразовать с помощью линейного ортогонального преобразования в новые переменные, при этом старые и новые переменные будут связаны , где U состоит из ортогональной и нормированной системы собственных векторов матрицы А квадратичной формы, при этом весовыми коэффициентами канонического представления являются собственный значения матрицы А.

Вопрос № 29: Знакоопределённые квадратичные формы многих переменных:

1. Знакоопределённые квадратичные формы многих переменных.

1) Критерии знакоопределенности.

1) Собственных значений.

2) Сильвестра.

Понятие знакоопределённости квадратичной формы используется для:

1. Определение типа кривой или поверхности второго порядка по её общему уравнению.

2. При исследовании функции многих переменных на экстремум, так как достаточным условием является знакоопределенность второго дифференциала.

Квадратичная форма называется положительно определённой, если она при любых ненулевых значениях своих аргументов принимает только положительные значения.

Если квадратичная форма меньше, либо равна нулю, то она отрицательно полу определена, иначе не определена.

Критерии знакоопределённости квадратичной формы:

Критерий собственных значений матрицы:

Приведём квадратичную форму к каноническому виду: , тогда для всех х – у не равно нулю, так как квадрат не нулевых чисел больше нуля. Ответственность за знак квадратичной формы несу её коэффициенты.

1. Если все собственные значения больше нуля, то квадратичная форма тоже больше нуля.

2. Если все собственные значения меньше нуля, то квадратичная форма тоже меньше нуля.

3. Если все собственные значения больше, либо равны нулю, то квадратичная форма тоже меньше нуля.

4. Если некоторые собственные значения равны нулю, а остальные меньше, то квадратичная форма отрицательно полу определена.

5. Если некоторые собственные значения больше нуля, а остальные меньше, то квадратичная форма может иметь любой знак.

Знакоопределённость квадратичной формы совпадает со знаками собственных значений её матрицы, то есть критерий собственных значений является полным, но трудоёмким, так как для вычисления собственных значений необходимо решить характеристическое уравнение матрицы.

Критерий Сильвестра:

Критерий Сильвестра позволяет выделить положительную и отрицательную знакоопределённость квадратичной формы с помощью вычисления нескольких определителей, являющихся угловыми минорами квадратичной формы.

После вычисления миноров суждение о знакоопределенности квадратичной формы выносится по следующему правилу:

1. Если все угловые миноры положительны, то квадратичная форма положительно определена.

2. Если угловые миноры чередуются знаком, начиная с минуса, то есть: ,то квадратичная форма отрицательно определена.

3. Если идёт чередование знаков, начиная с плюса, или любое другое сочетание знаков, или существуют миноры, равные нулю (последний минор не равен нулю), то форма знака неопределенна.

4. Если последний минор равен нулю, в этом случае критерий Сильвестра не различает знакоопределённости формы, и необходимо использовать другой критерий.

Это свидетельствует о грубости метода.