1) Свойства.

2. Теорема о существовании линейно независимых решений.

1) Доказательство.

Система называется однородной, если все свободные члены равны нулю.

Однородная система всегда совместна. Существует только одно решение.

Теорема о существовании не нулевых решений однородной системы:

Однородная система имеет не нулевые решения тогда, когда ранг матрицы коэффициентов меньше числа неизвестных.

Доказательство:

Не единственность решения

Однородная система с одинаковым количеством уравнений и неизвестных имеет не нулевые решения тогда, когда определитель матрицы коэффициентов не равен нулю.

Теорема:

Любая линейная комбинация решений однородной системы сама является её решением:

Доказательство:

Пусть существуют два решения,

Теорема о существовании линейно независимых решений:

Путь ранг системы равен рангу матрицы коэффициентов и меньше числа неизвестных, тогда существует число линейно независимых решений, равное разности количества переменных и ранга системы.

Доказательство:

Пусть базисный минор содержится в левом верхнем углу матрицы.

Строки, не входящие в базисный минор можно отбросить, а свободные неизвестные перенести через знак равенства.

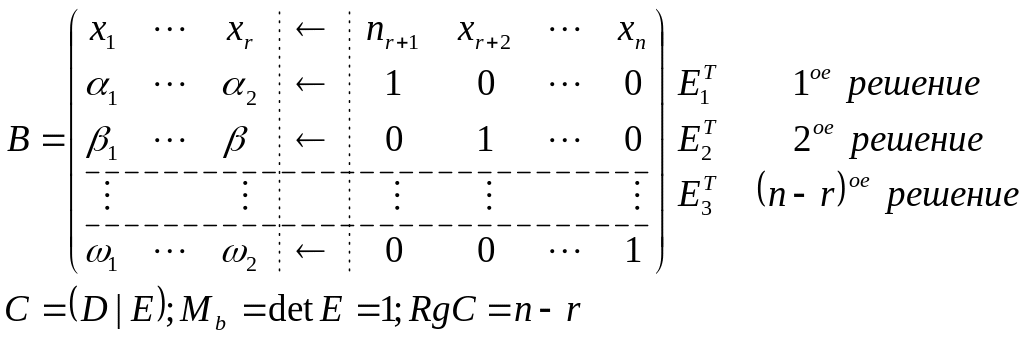
Вопрос № 14: Фундаментальная система решений однородной системы уравнений:

1. Фундаментальная система решений однородной системы уравнений.

2. Структура общего решения однородной и не однородной системы уравнений.

Структура общего решения однородной системы уравнений:

ФСР называется система из n-r линейно независимых частных решений

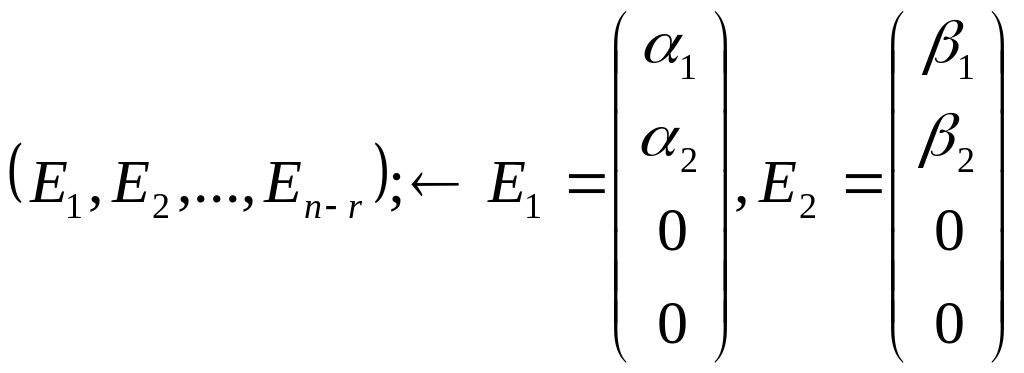
Теорема: Общее решение однородной системы уравнений:

Общим решением однородной системы линейных уравнений является линейная комбинация столбцов фундаментального решения.

Структура общего решения не однородной системы уравнений:

Рассмотрим систему линейных уравнений: Неоднородная система , однородная система:

Теорема:

Разность двух решений неоднородной системы является решением соответствующей однородной системы.

Доказательство:

Пусть столбец α является решением неоднородной системы , β – решение системы , тогда после вычитания одного из другого получим: удовлетворяет однородной системе. Из теоремы следует, что общее решение однородной системы является суммой какого-либо её частного решения и общего решения соответствующей однородной системы

Вопрос № 15: Собственные векторы и собственные значения матрицы:

1. Собственные векторы матрицы.

2. Собственные значения матрицы.

1) Определение.

2) Свойства.

Арифметическим собственным вектором квадратной матрицы А порядка п называется такой не нулевой столбец: , где λ – собственной значение матрицы.

У каждой матрицы может быть пара из собственных векторов и собственных значений.

Множество всех собственных значений матрицы называется спектром. 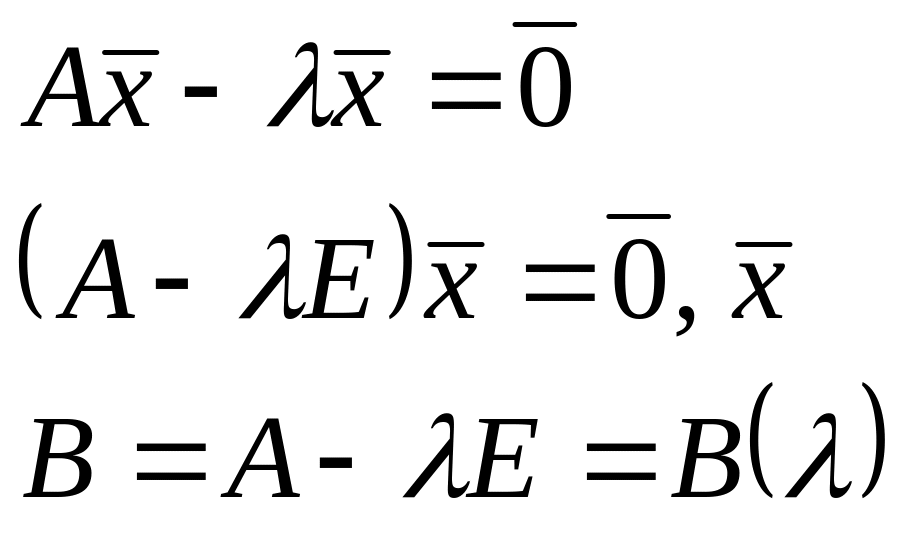– ненулевые решения однородной системы уравнений.

Однородная система имеет ненулевые решения, если ранг матрицы В равен количеству коэффициентов.

– характеристическое уравнение матрицы А.

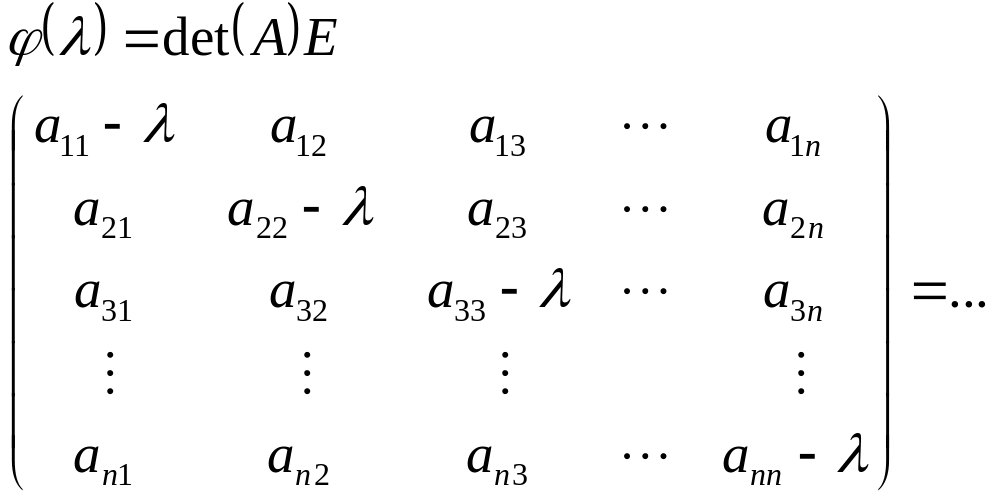Проверить!!!¿¿¿

Рациональное алгебраическое уравнение степени N. Всегда имеет N корней, среди которых могут быть и кратные. Проверить!!!¿¿¿

Если определитель матрицы А равен нулю, то характеристический многочлен не содержит свободных членов.

У вырожденной матрицы хотя бы одно значение равно нулю. ¿¿¿

…???

При этом сами фундаментальные решения образуют систему линейно независимых уравнений.

Свойства собственных векторов и собственных значений матрицы:

1. Максимальное количество линейно независимых собственных векторов, соответствующих данному собственному значению .

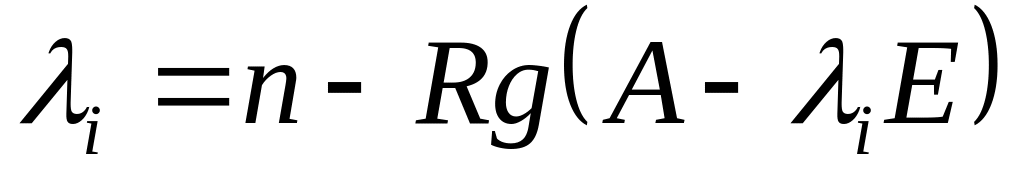2. Линейная комбинация из собственных векторов соответствует одному и тому же, в свою очередь являющемуся собственным вектором для этого собственного значения.

3. Собственные векторы с попарно различными «чего-то такое???» значениями являются ??? Проверить¿¿¿

4. Если матрица А^Т=А, то все её собственные значения являются действительными числами.

5. Спектр вырожденной матрицы А содержит хотя бы один нулевой элемент.

6. Если матрица имеет пары ??? комплексные сопряженные ¿¿¿,!!! То соответствующие им собственные векторы тоже комплексные.

Вопрос № 16: Нахождение собственных векторов и собственных значений матрицы:

Для вычисления собственных значений матрицы необходимо составить характеристическое уравнение: составив уравнение можно найти его корни, они-то и будут собственными значениями матрицы.

Собственные векторы матрицы соответствуют собственным значениям матрицы.

Вопрос № 17: Линейные операции над векторами:

1. Линейные операции над векторами.

2. Базис.

3. Координаты вектора.

4. Аффинная система координат.

1) На плоскости.

2) В пространстве.

5. Прямоугольная система координат.

1) На плоскости.

2) В пространстве.

Аналитическая геометрия – это методы решения геометрических задач с помощью аналитических операций.

Векторная алгебра:

1. Геометрическим вектором называется направленный отрезок прямой, который можно переносить параллельно самому себе.

2. Модулем вектора называется его длина.

3. Нулевым вектором называется вектор, начало и конец которого совпадают.

4. Коллинеарными называются вектора, лежащие на параллельных прямых.

5. Равными называются коллинеарные, со направленные вектора, имеющие одинаковую длину.

6. Компланорными называются векторы, расположенные в одной и той же, или в параллельных плоскостях.

Линейные операции над векторами:

1. Сложение:

2. Умножение на число: Вектор, умноженный на минус единицу меняет своё направление на противоположенное.

3. Вычитание: – это сложение с вектором, умноженным на минус единицу.

Теорема о взаимной колиниарности векторов:

Для всех векторов а, не равных нулю, все вектора в колиниарны а, то вектор в можно представить, как произведение вектора а на некоторое ненулевое число.

Свойства линейных операций над векторами:

1. 

2. 

3. 

4. 

Линейная зависимость и независимость геометрических векторов:

Линейной комбинацией геометрических векторов называется вектор

Системой из N векторов называется линейно независимой, если ни один из них не является и не может быть представлен в виде линейной комбинации других векторов этой системы.

Если линейная комбинация всех этих векторов является нулевым вектором, то в случае равенства нулю всех «С»: , иначе если “C_i” не равно нулю, то система векторов называется линейно зависимой.

Теорема №1:

Два колиниарных вектора всегда линейно зависимы.

Теорема №2:

Три комплонарных вектора всегда линейно зависимы.

Теорема №3:

Любые четыре геометрических вектора линейно зависимы.

Базис:

Базисом на плоскости, или в пространстве называется максимальная система из линейно независимых векторов.

1. Базис на прямой является единственным вектором, параллельным данной прямой.

2. Базис на плоскости – это любая пара из не коллинеарных векторов, параллельных этой плоскости.

3. Базис в пространстве – это любые три не комплонарных вектора.

Разложение вектора по базису называется представление его в виде линейной комбинации векторов базиса.

Теорема:

Для заданного вектора а и выбранного базиса разложение, по базису является единственным.

Координаты вектора в базисе:

Координатами любого вектора в пространстве (в базисе) называются коэффициенты его разложения базису.

Свойства:

При сложении векторов одного и того же базиса, складываются соответствующие координаты.

При умножении вектора на число, умножаются все координаты этого вектора число.

Системы координат на плоскости и в пространстве:

Аффинная система координат:

Аффинной системой координат называется совокупность из точки – начала координат, и базиса.

Не аффинная система координат:

Не аффинной системой координат является полярная (цилиндрическая, сферическая) система координат.

Декартова система координат:

Частным случаем аффинной системы координат является прямоугольная Декартова система координат.

Вопрос № 18: Скалярное произведение векторов:

1. Скалярное произведение векторов.