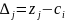МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ РОССИИ
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ РОССИИ
Федеральное государственное
бюджетное образовательное учреждение
высшего профессионального образования
«Комсомольский - на- Амуре государственный
технический университет»
Институт КП МТО
Кафедра « Технология сварочного производства»
Расчетно-графические задание
по дисциплине «Специальные методы восстановления деталей машин»
Вариант № 1
Студент группы 7ОС-1 В.С. Пицык
подпись дата
Преподаватель С.В. Ланкина
подпись дата
2011
 Исходные
данные
Исходные
данные
Задание 1
Предприятие производит четыре вида деталей с использованием 4 видов ресурсов. Прибыль от продажи первого вида детали составляет 4 ден.ед., второго вида – 5 ден.ед., третьего – 7 ден.ед., четвертого – 9 ден.ед. Исходные данные необходимые для решения задачи приведены в таблице 1. По приведенным данным необходимо найти:
Построить математическую модель задачи, при условии максимальной прибыли;
Записать стандартную (каноническую) форму задачи;
Решить задачу симплекс-методом.
Таблица 1 – Исходные данные для задания 1
Ресурс |
Деталь |
Запас ресурсов |
|||
I |
II |
III |
IV |
||
I |
1 |
7 |
5 |
2 |
550 |
II |
3 |
1 |
0 |
4 |
350 |
III |
0 |
3 |
6 |
2 |
650 |
IV |
4 |
2 |
5 |
2 |
650 |
Задание 2
В
результате экспериментов были получены
данные, которые представлены в таблице
2. Способом наименьших квадратов подобрать
для заданных значений x
и y
квадратичную функцию
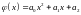 .
Построить на одной координатной плоскости
экспериментальные данные и аппроксимирующую
функцию.
.
Построить на одной координатной плоскости
экспериментальные данные и аппроксимирующую
функцию.
 Таблица
2 – Исходные данные для задания 2
Таблица
2 – Исходные данные для задания 2
х |
87,5 |
84,0 |
77,8 |
63,7 |
46,7 |
36,9 |
у |
292 |
283 |
270 |
235 |
197 |
181 |
Задание 3
Пусть
заданы значение xi0
каждого фактора на нулевом уровне,
интервал варьирования i
– го фактора, а также результаты опытов.
Параметр, подлежащий оптимизации
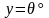 – некоторый угол. Обрабатываемый
материал сталь 10Х15Н27Т3МР. Переменные
факторы: x10
= 80 м/мин; Δ
x1
= 10 м/мин; x20
= 0,3 мм/об; Δ
x2
= 0,09 мм/об; x30
= 4,5 мм; Δ
x3
= 0,5 мм. Проводятся
по две серии параллельных опытов (m
=
2). Результаты эксперимента приведены
в таблице 3. Необходимо:
– некоторый угол. Обрабатываемый
материал сталь 10Х15Н27Т3МР. Переменные
факторы: x10
= 80 м/мин; Δ
x1
= 10 м/мин; x20
= 0,3 мм/об; Δ
x2
= 0,09 мм/об; x30
= 4,5 мм; Δ
x3
= 0,5 мм. Проводятся
по две серии параллельных опытов (m
=
2). Результаты эксперимента приведены
в таблице 3. Необходимо:
Определить значения коэффициентов
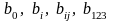 ;
;Провести проверку воспроизводимости эксперимента;
Рассчитать оценки коэффициентов регрессии, определить дисперсии оценок коэффициентов, проверить их значимость;
Проверить адекватность полученного математического описания.
Таблица 3 – Результаты эксперимента (исходные данные для задания 3)
Параметр |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
y1 |
981,7 |
930,0 |
673,3 |
876,0 |
826,7 |
842,7 |
775,0 |
1005 |
y2 |
986,0 |
912,0 |
654,2 |
878,7 |
881,8 |
891,2 |
757,8 |
1006,7 |
 Решение
к заданию 1
Решение
к заданию 1
1.
Производится 4 вида продукции с
использование 4 видов ресурсов. Обозначим
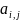 – расход i-го
ресурса на производство единицы j-й
продукции. Тогда матрица расходов
ресурсов будет иметь вид:
– расход i-го
ресурса на производство единицы j-й
продукции. Тогда матрица расходов
ресурсов будет иметь вид:
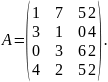
2.
Обозначим через
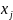 – объем j-й
продукции. Тогда целевая функция бед
иметь вид:
– объем j-й
продукции. Тогда целевая функция бед
иметь вид:
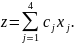
Составим
ограничение для каждого из ресурсов.
Расход первого ресурса на производство
продукции всех 4-х видов (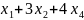 )
не должен превышать имеющегося запаса
– 550 единиц, т.е.
)
не должен превышать имеющегося запаса
– 550 единиц, т.е.
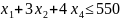 .
.
Аналогично, записывая ограничения для 2-го, 3-го и 4-го ресурсов, а также принимая во внимание то, что объем выпуска каждого вида продукции не может быть отрицательным, получим систему ограничений:
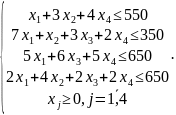
3. Добавляя в систему ограничений балансовые переменные, мы получим стандартную форму задачи оптимизации производства:
Найти
значения переменных
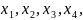 при которых:
при которых:
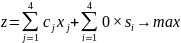
 при
условиях
при
условиях
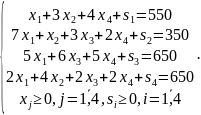
4.
В начальном плане считаем, что базисными
переменными являются балансовые
переменные:
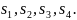 Пологая, что
Пологая, что
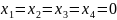 ,
тогда из системы ограничений получим
,
тогда из системы ограничений получим
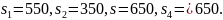 При этом значение целевой функции z
= 0. На основании вышесказанного постоим
симплекс-таблицу 1.1.
При этом значение целевой функции z
= 0. На основании вышесказанного постоим
симплекс-таблицу 1.1.
Таблица 1.1 – Исходная симплекс-таблица
|
|
|
4 |
5 |
7 |
9 |
0 |
0 |
0 |
0 |
|
i |
|
Базис |
|
|
|
|
|
|
|
|
Решение
|
1 |
0 |
|
1 |
3 |
0 |
4 |
1 |
0 |
0 |
0 |
550 |
2 |
0 |
|
7 |
1 |
3 |
2 |
0 |
1 |
0 |
0 |
350 |
3 |
0 |
|
5 |
0 |
6 |
5 |
0 |
0 |
1 |
0 |
650 |
4 |
0 |
|
2 |
4 |
2 |
2 |
0 |
0 |
0 |
1 |
650 |
|
-4 |
-5 |
-7 |
-9 |
0 |
0 |
0 |
0 |
0 |
||

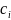
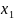
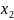
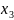
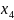
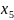 (
(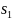 )
)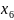 (
(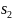 )
)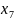 (
(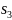 )
)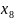 (
( )
)