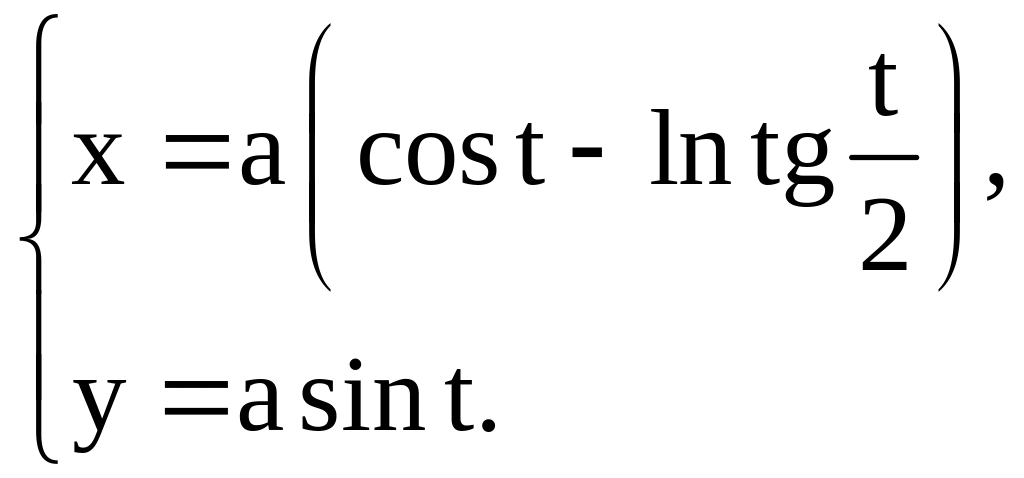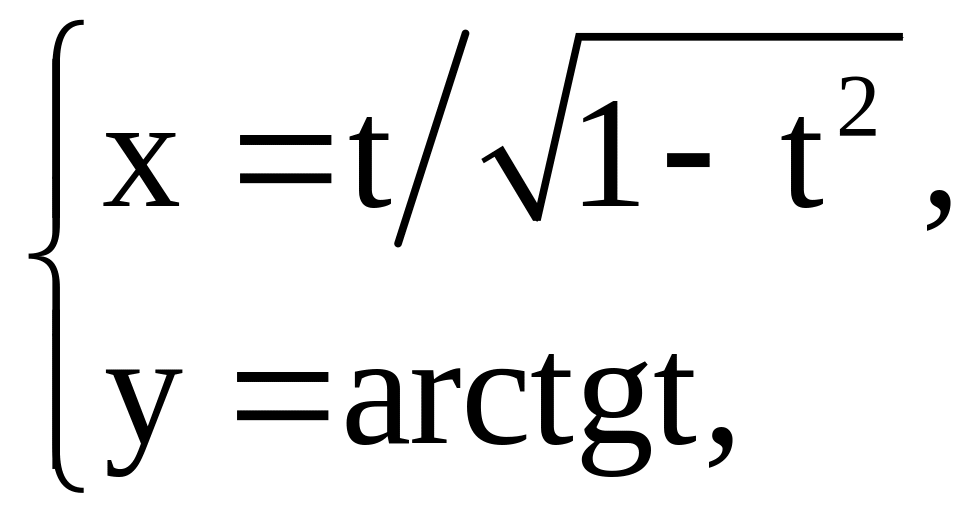Задание 5.14
Найдите производные 1-го и 2-го порядков от функций, заданных параметрически.
1) |
10) |
19) |
2) |
11) |
20) |
3) |
12) |
21) |
4) |
13) |
22) |
5) |
14) |
23) |
6) |
15) |
24) |
7) |
16) |
25) |
8) |
17) |
26) |
9) |
18) |
27) |
28) |
29) |
30) |
Задание 5.15
Используя дифференциал первого порядка, найдите приближённо (ln2 0,693, ln3 1,099, ln5 1,609, 3,1416).
1)
![]() ;
7)
;
7)
![]() ;
13) arctg 1,05; 19)
;
13) arctg 1,05; 19)
![]() ;
25) arcsin 0,05;
;
25) arcsin 0,05;
2)
![]() ;
8) 32,1; 14)
;
8) 32,1; 14)
![]() ; 20)
arctg 0,9; 26)
; 20)
arctg 0,9; 26)
![]() ;
;
3)
cos 1; 9) 51,9;
15)
![]() ; 21)
; 21)
![]() ;
27) tg 1;
;
27) tg 1;
4)
41,8;
10)
![]() ;
16) sin 320; 22)
;
16) sin 320; 22)
![]() ;
28) tg 440;
;
28) tg 440;
5)
23,1;
11) cos 310;
17)
![]() ;
23) 31,8;
29) ctg 470;
;
23) 31,8;
29) ctg 470;
6)
arctg 1,2; 12) sin 880;
18) 23,8; 24)
cos 930;
30)
![]() .
.
Задание 5.16
С помощью формулы Тейлора найдите приближённое значение числа с точностью до 0,001.
1) e2; |
7) cos3/2; |
13) ln4; |
19) sin2; |
25) arctg2; |
2)
|
8) sin3/2; |
14) ln5; |
20) cos2; |
26) arctg3; |
3) e3/2; |
9) cos1; |
15) ln6; |
21) sin3; |
27) arctg3/2; |
4) e5/2; |
10) sin4; |
16)
|
22) cos3; |
28) arctg 5/2; |
5)
|
11) sin5/2; |
17) cos4; |
23) arctg 7/2; |
29) e3; |
6) sin 7/2; |
12)
|
18) cos 9/2; |
24) arctg 4; |
30) sin5. |
Задание 5.17
Найдите площадь треугольника, образованного прямой
![]() ,
касательной и нормалью, проведёнными
к графику заданной функции в точке с
заданной абсциссой x0
или в точке, соответствующей значению
параметра t0.
,
касательной и нормалью, проведёнными
к графику заданной функции в точке с
заданной абсциссой x0
или в точке, соответствующей значению
параметра t0.
1)
![]() ; 3)
; 3)
![]() ;
;
2)
 4)
4)
![]() ;
;
5)
![]() ; 18)
; 18)

6)
![]() ; 19)
; 19)
![]() ;
;
7)
 20)
20)
![]() ;
;
8)
![]() ;
21)
;
21)

9)
![]() ; 22)
; 22)
![]() ;
;
10)
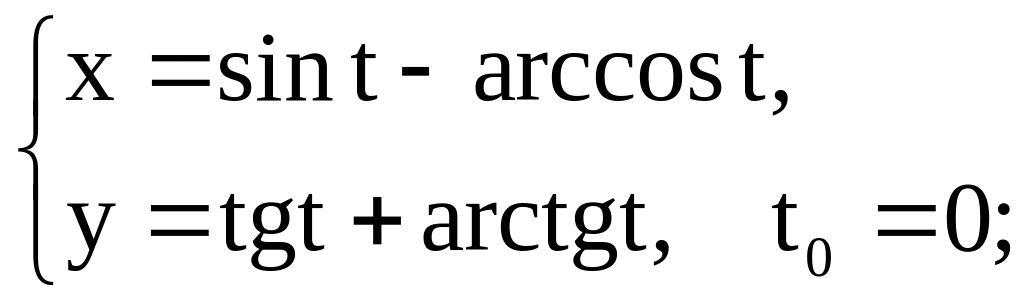 23)
23) ![]() ;
;
11)
![]() ; 24)
; 24)
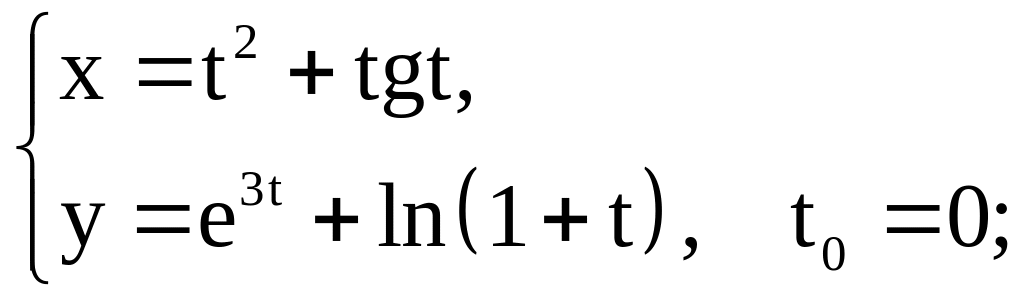
12)
![]() ; 25)
; 25)
![]() ;
;
13)
 26)
26)
![]() ;
;
14)
![]() ; 27)
; 27)
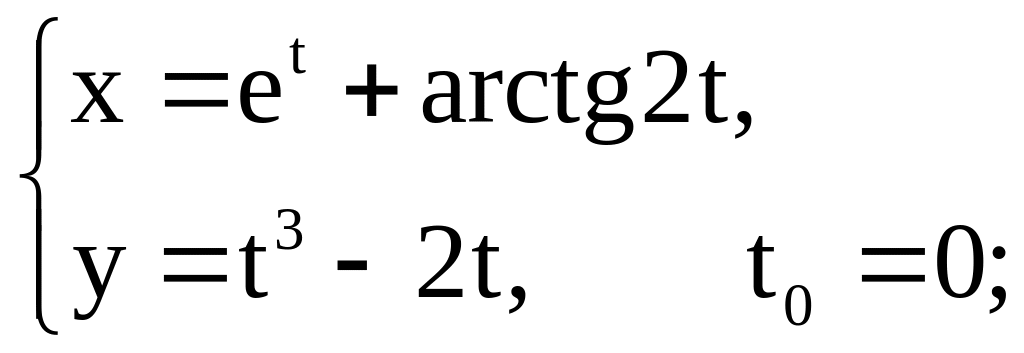
15)
![]() ; 28)
; 28)
![]() ;
;
16)
 29)
29)
![]() ;
;
17)
![]() ; 30)
; 30)

Задание 5.18
Пользуясь правилом Лопиталя, найдите пределы.
1.
a)
 , б)
, б)
 ;
;
2.
a)
![]() , б)
, б)
 ;
;
3.
a)
![]() , б)
, б)
 ;
;
4.
a)
 , б)
, б)
![]() ;
;
5.
a)
 , б)
, б)
 ;
;
6.
a)
![]() , б)
, б)
 ;
;
7.
a)
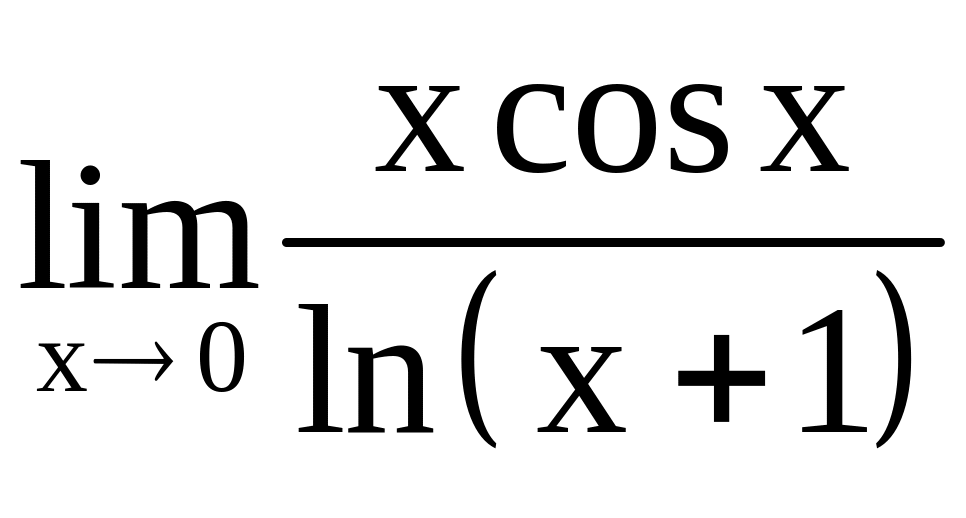 , б)
, б)
 ;
;
8.
a)
 , б)
, б)
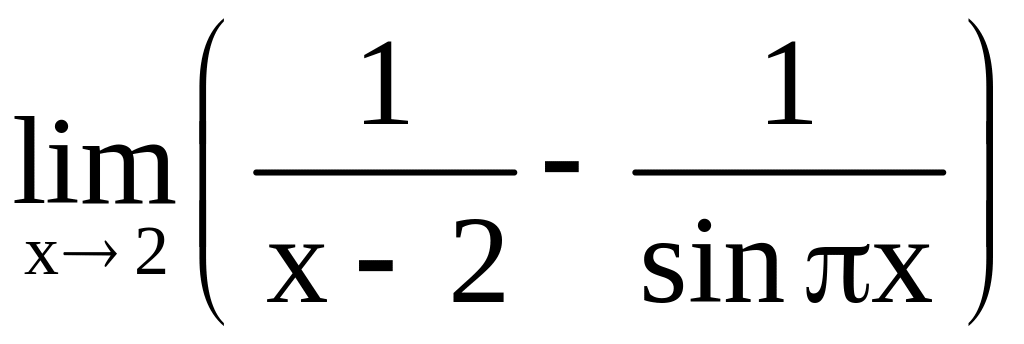 ;
;
9.
a)
![]() , б)
, б)
 ;
;
10.
a)
 , б)
, б)
 ;
;
11.
a)
![]() , б)
, б)
 ;
;
12.
a)
 , б)
, б)
 ;
;
13.
a)
 , б)
, б)
 ;
;
14.
a)
![]() , б)
, б)
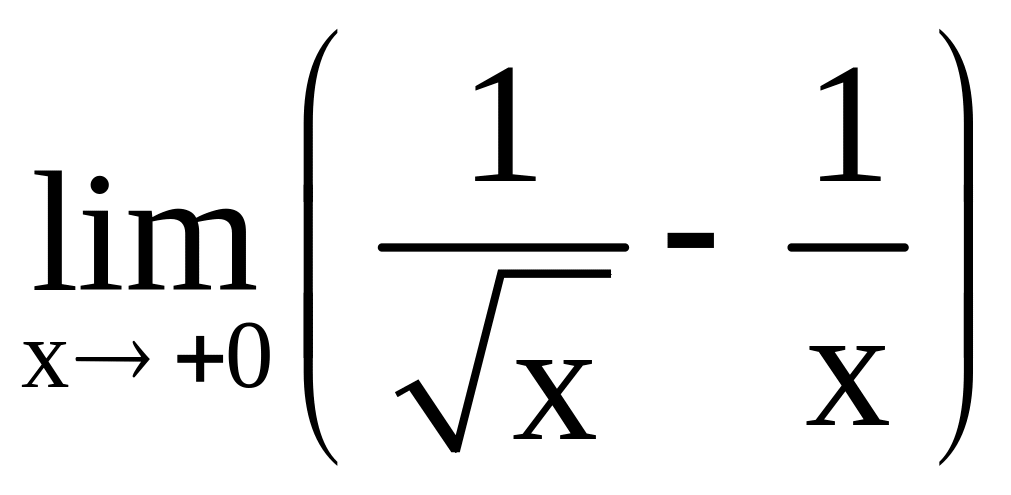 ;
;
15.
a)
![]() , б)
, б)
 ;
;
16.
a)
 , б)
, б)
 ;
;
17.
a)
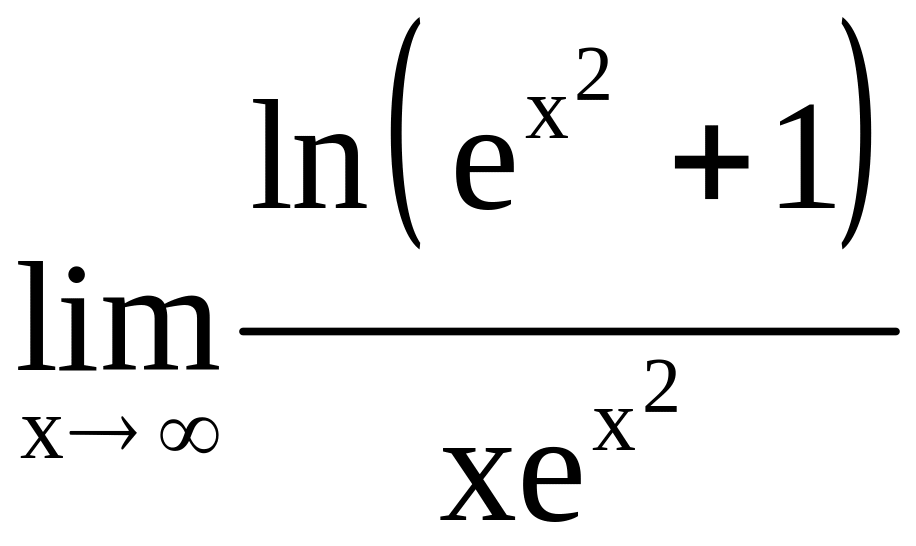 , б)
, б)
 ;
;
18.
a)
 , б)
, б)
 ;
;
19.
a)
 , б)
, б)
 ;
;
20.
a)
 , б)
, б)
 ;
;
21.
a)
 , б)
, б)
 ;
;
22.
a)
 , б)
, б)
 ;
;
23.
a)
 , б)
, б)
 ;
;
24.
a)
![]() , б)
, б)
 ;
;
25.
a)
 , б)
, б)
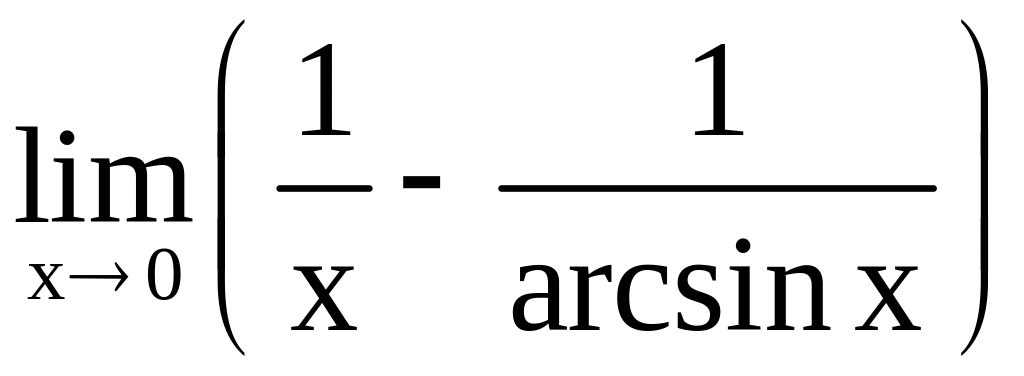 ;
;
26.
a)
 , б)
, б)
 ;
;
27.
a)
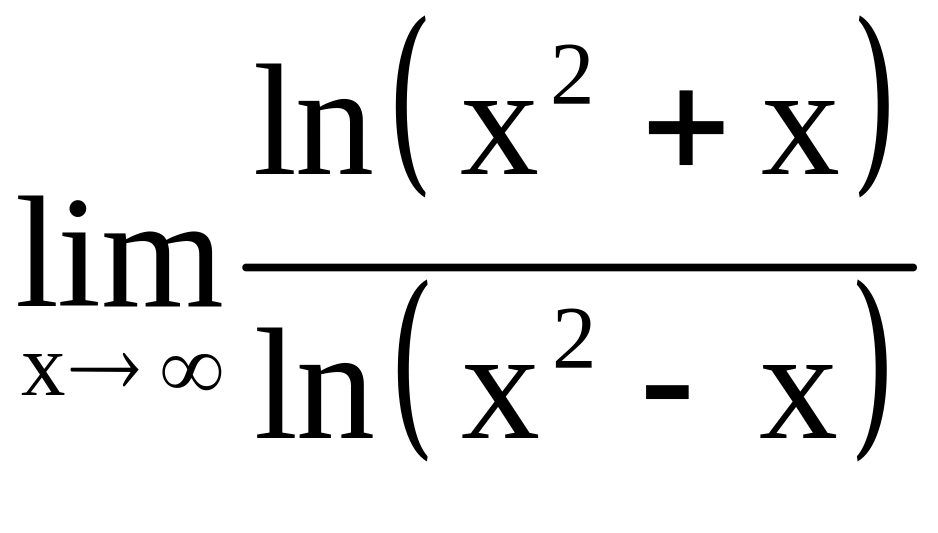 , б)
, б)
 ;
;
28.
a)
 , б)
, б)
 ;
;
29.
a)
![]() , б)
, б)
 ;
;
30.
a)
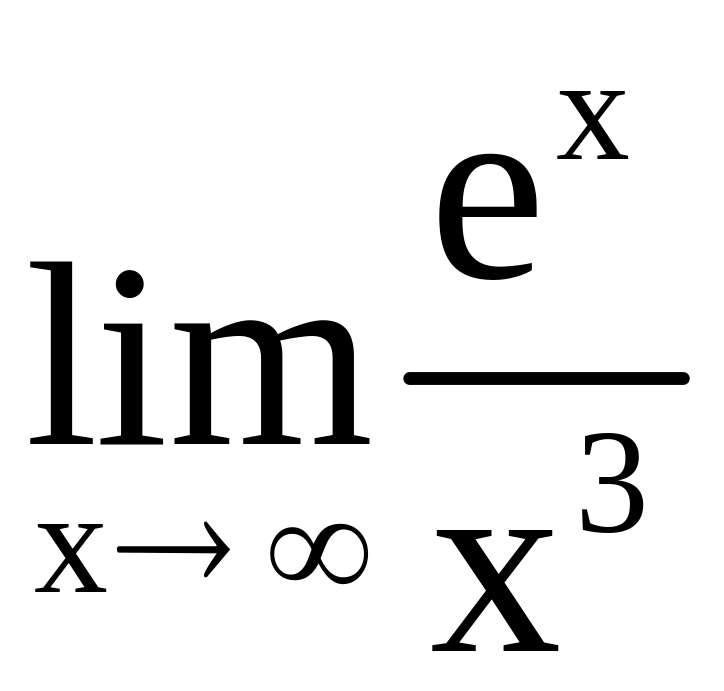 , б)
, б)
 .
.
VI. Исследование функции. Построение графика функции
1. Возрастание и убывание функции. Точки экстремума
Говорят,
что функция
![]() возрастает (убывает) на интервале
возрастает (убывает) на интервале
![]() ,
если для любых различных точек
,
если для любых различных точек
![]() ,
,![]() из
справедливо
неравенство
из
справедливо
неравенство
![]()
![]() ,
т.е. если большему значению аргумента
соответствует большее (меньшее) значение
функции.
,
т.е. если большему значению аргумента
соответствует большее (меньшее) значение
функции.
Теорема 1.
Если функция f(x) дифференцируема на
(a; b) и
![]() (
(![]() )
для любого
)
для любого
![]() ,
то f(x) возрастает (убывает) на (a, b).
,
то f(x) возрастает (убывает) на (a, b).
Точка x0 называется точкой максимума (минимума) функции f(x), определённой в некоторой окрестности x0, если существует некоторая окрестность (x0 – ; x0 + ) этой точки, такая, что для любого x(x0 – ; x0 + ), x x0 справедливо неравенство f(x) < f(x0) (f(x) > f(x0)); при этом f(x0) называют максимумом (минимумом) функции. Точки максимума и точки минимума называют точками экстремума.
Теорема 2
(необходимое
условие экстремума).
Если функция f(x) дифференцируема в
промежутке (a,b) и x0(a,
b) является точкой экстремума f(x), то
![]() .
.
Точки, в которых , называются стационарными точками f(x). Не всякая стационарная точка является точкой экстремума.
Теорема 3
(достаточное
условие экстремума).
Пусть функция f(x) дифференцируема в
окрестности стационарной точки x0.
Если при переходе через точку x0
![]() меняет свой знак, то x0
является точкой экстремума. А именно,
если при переходе через точку x0
:
меняет свой знак, то x0
является точкой экстремума. А именно,
если при переходе через точку x0
:
а) меняет свой знак
с минуса на плюс (т.е.
![]() при достаточно малых значениях
при достаточно малых значениях
![]() ),
то x0
является точкой минимума;
),
то x0
является точкой минимума;
б) меняет свой знак
с плюса на минус (т.е.
![]() при достаточно малых значениях
),
то x0
является точкой максимума функции;
при достаточно малых значениях
),
то x0
является точкой максимума функции;
в) не меняет своего знака, то x0 не является точкой экстремума.
Иногда удобно пользоваться другим достаточным условием экстремума.
Теорема 4
(достаточное условие экстремума).
Пусть x0
– стационарная точка функции f(x), дважды
дифференцируемой в точке x0.
Если
![]() ,
то x0
является точкой экстремума. Точнее
говоря, если: а)
,
то x0
является точкой экстремума. Точнее
говоря, если: а)
![]() ,
то x0
– точка минимума; б)
,
то x0
– точка минимума; б)
![]() ,
то x0
– точка максимума.
,
то x0
– точка максимума.
Точкой экстремума f(x) может оказаться и точка, в которой не определена. Стационарные точки и точки, в которых не определена, называют критическими точками функции.
Пример 1.
Найти точки экстремума функции
 .
.
Р ешение.
Наша функция дифференцируема на всей
числовой оси. Найдём стационарные точки.
ешение.
Наша функция дифференцируема на всей
числовой оси. Найдём стационарные точки.
![]() .
Стационарными точками являются
.
Стационарными точками являются
![]() .
При переходе через точку
.
При переходе через точку
![]() не меняет своего знака, поэтому эта
точка не является точкой экстремума.
При переходе через точку
не меняет своего знака, поэтому эта
точка не является точкой экстремума.
При переходе через точку
![]() меняет свой знак с «–» на «+», следовательно,
– точка минимума (на рисунке получается
«впадина»).
меняет свой знак с «–» на «+», следовательно,
– точка минимума (на рисунке получается
«впадина»).
Для нахождения
наибольшего и наименьшего значений
функции на отрезке
![]() находят значения функции в критических
точках, принадлежащих этому отрезку, и
на концах отрезка, после чего сравнивают
эти значения и выбирают наибольшее и
наименьшее.
находят значения функции в критических
точках, принадлежащих этому отрезку, и
на концах отрезка, после чего сравнивают
эти значения и выбирают наибольшее и
наименьшее.
Пример
2. Найти
наибольшее и наименьшее значения функции
![]() на отрезке [–1; 3].
на отрезке [–1; 3].
Решение. Функция дифференцируема на всей числовой оси. Найдём стационарные точки
![]() .
.
Стационарными точками являются x1 = –2, x2 = 0, x3 = 2; из них лишь x2 = 0 и x3 = 2 принадлежат промежутку [–1; 3] . Найдём значения функции в точках x = 0, x = 2, а также на концах отрезка: f(0) = 0,
f(2) =16 – 32 = –16, f(–1) = 1 – 8 = –7, f(3) = 81 – 72 = 9. Сравнив полученные значения, находим:
![]() ,
,
![]() .
.