Найдём
:
.
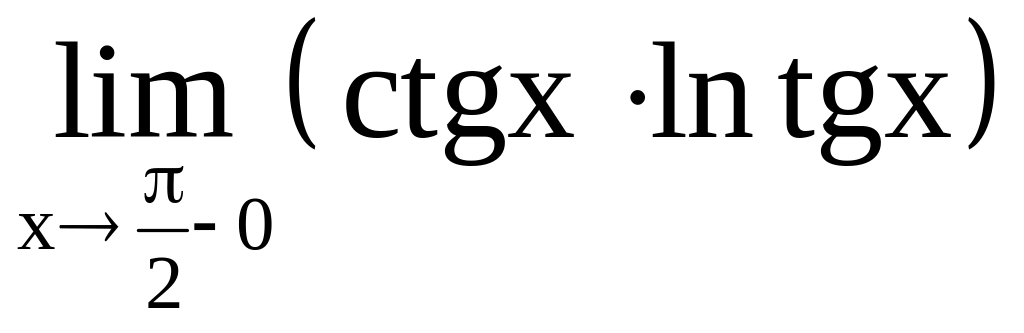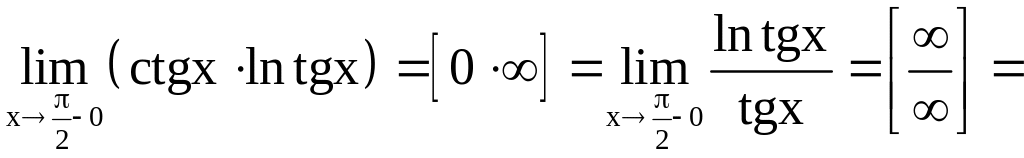
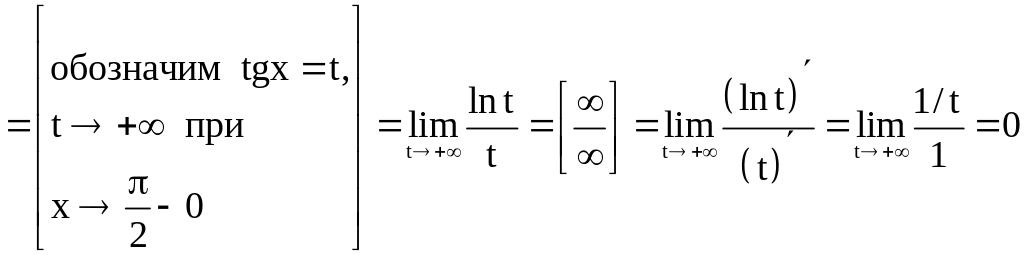Итак,
.
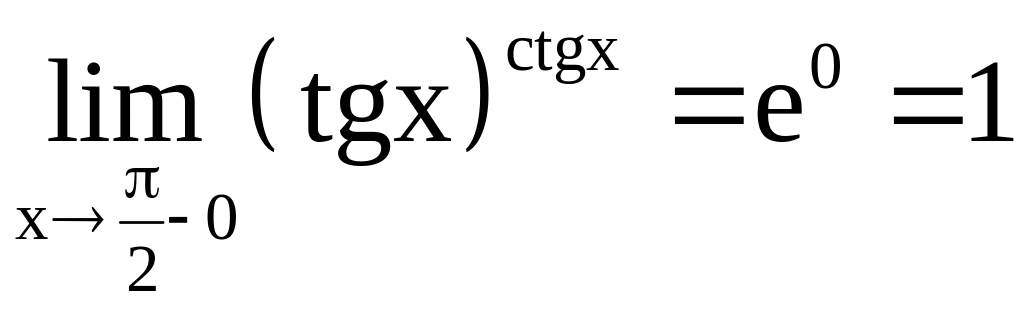д) Имеем
неопределённость вида
.
Переведём эту неопределённость в
неопределённость вида
и затем воспользуемся правилом Лопиталя:
.
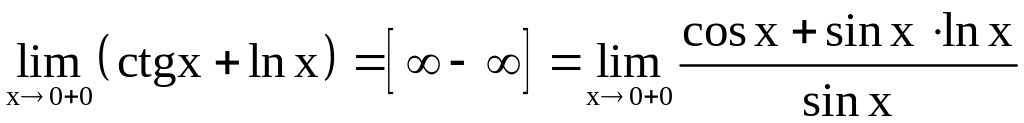А так как
,
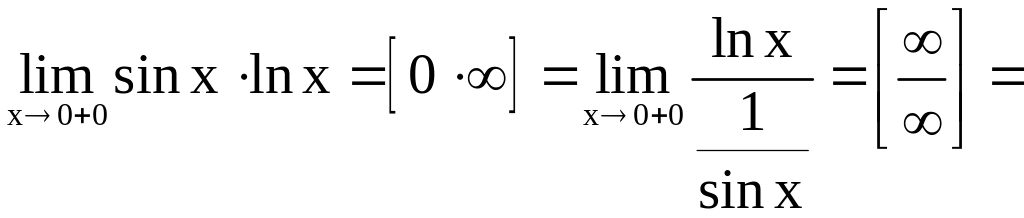
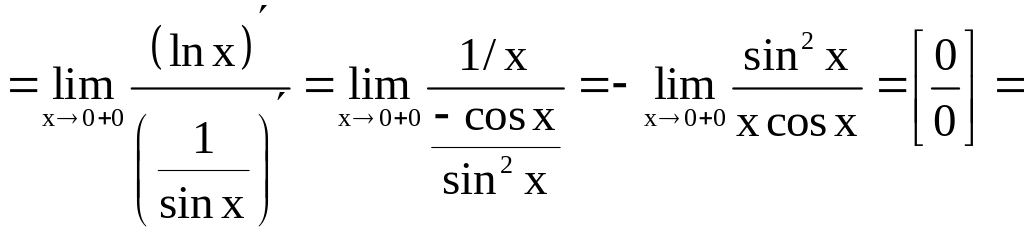
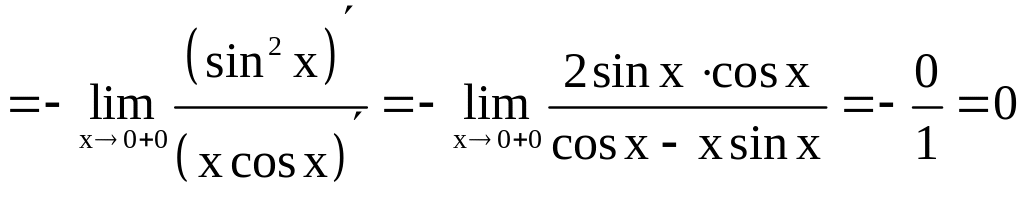то
.
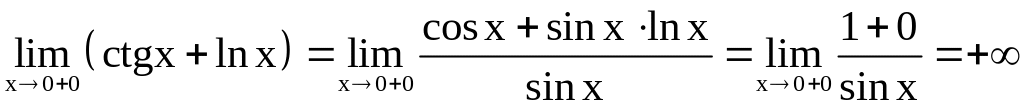Задание 5.1
Используя определение производной, найдите производную функции.
1) y = x sin (2x + 3); |
16) y = (x + 3) lnx; |
2) y = (4x – 1) ln (2x); |
17)
|
3) y = cos (2x2 + x +1); |
18) y = 4x e3x; |
4)
|
19) y = e4x sin 2x; |
5) y = x e4x ; |
20)
|
6) y = ex sin3x; |
21) y = (2x2 – x +2) sinx; |
7)
|
22) y = x cos (3x – 1); |
8) y = (x2 + 3x +1) sinx; |
23)
|
9) y = cos (x2 – x +2); |
24) y = e3x cosx; |
10) y = 3x cos (x + 4); |
25) y = (3x2 + x +1) cosx; |
11)
|
26) y = (x2 – 2x +3); |
12) y = e2x cos4x; |
27) y = x sin (4x + 3); |
13) y = (x2 – x + 2) cosx; |
28) y = (3x – 1) ln 2x; |
14) y = sin (x2 + 3x +2); |
29)
|
15) y = 4x sin (x – 2); |
30) y = 2x e4x . |
;
;
;
;
;
;
;
Задание 5.2
Найдите производную первого порядка от функции.
1)
|
14)
|
2)
|
15)
|
3)
|
16)
|
4)
|
17)
|
5)
|
18)
|
6)
|
19)
|
7)
|
20)
|
8)
|
21)
|
9)
|
22)
|
10)
|
23)
|
11)
|
24)
|
12)
|
25)
|
13)
|
26)
|
27)
|
29)
|
28) |
30)
|
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
.Задание 5.3
Найдите производную первого порядка от функции.
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
.
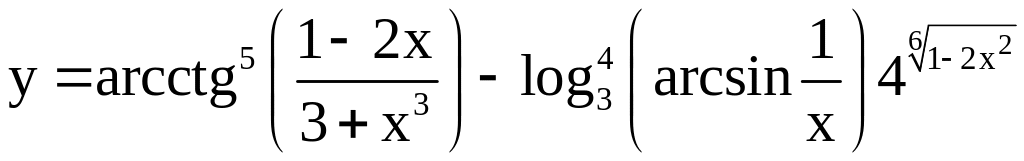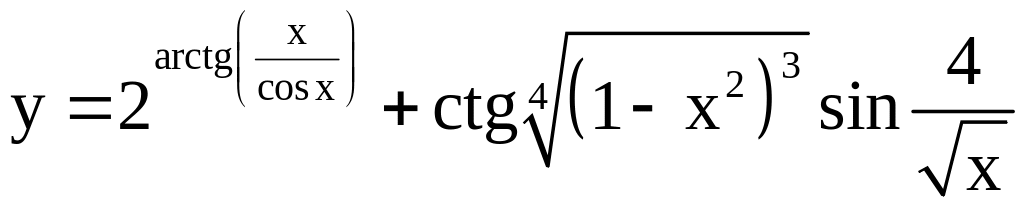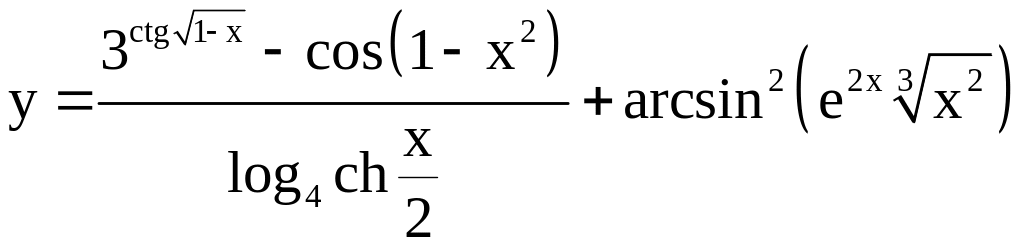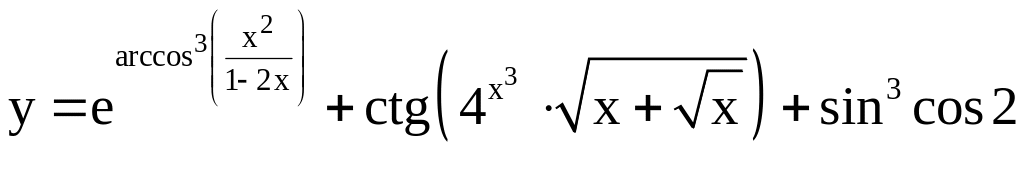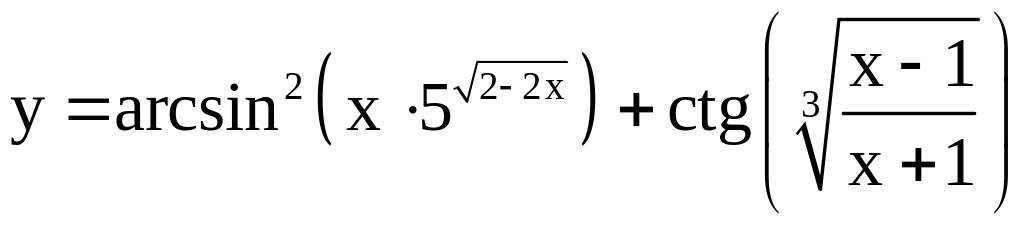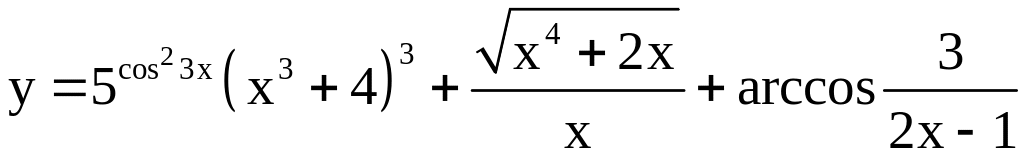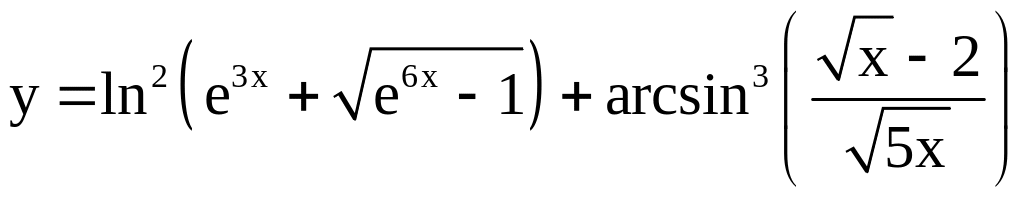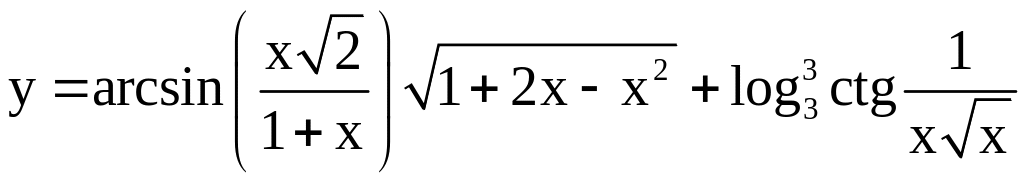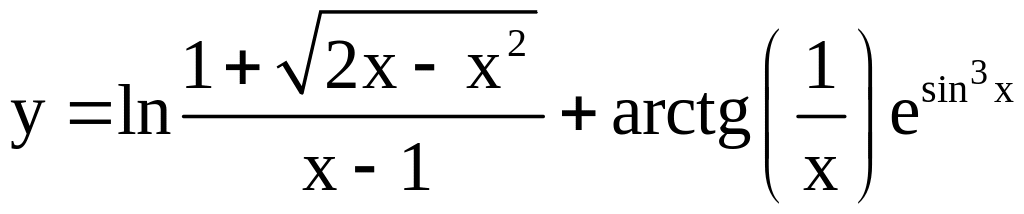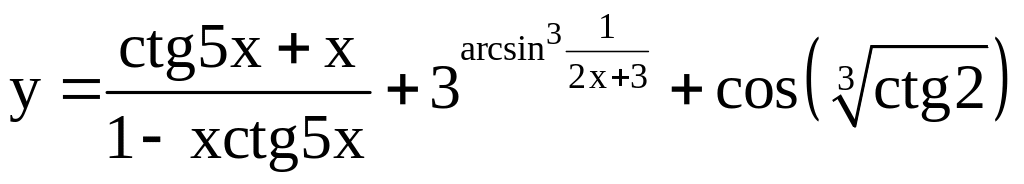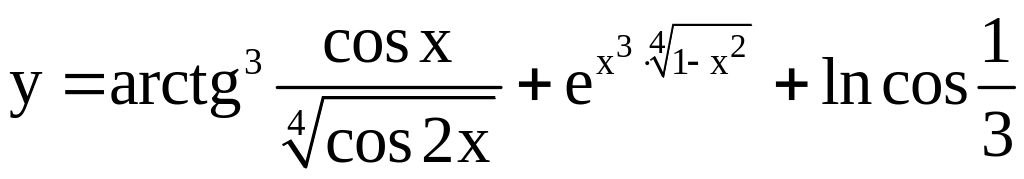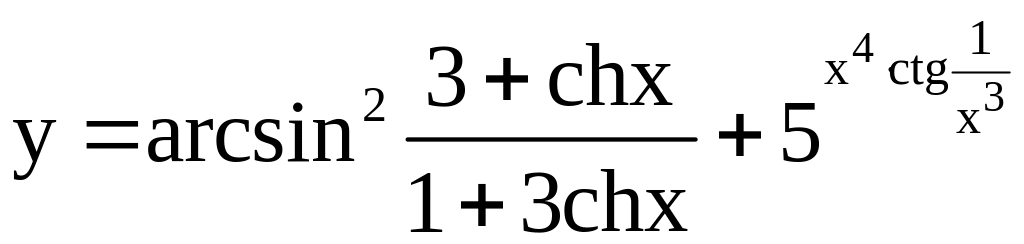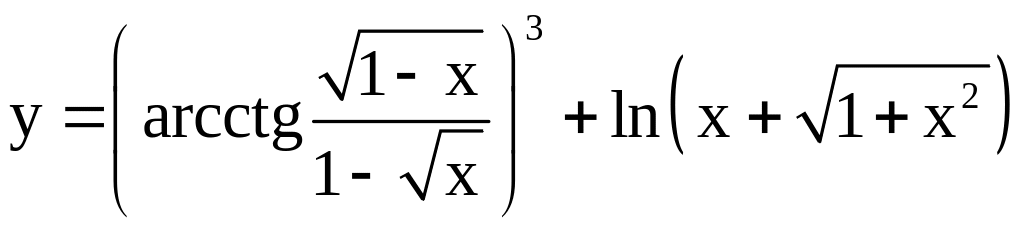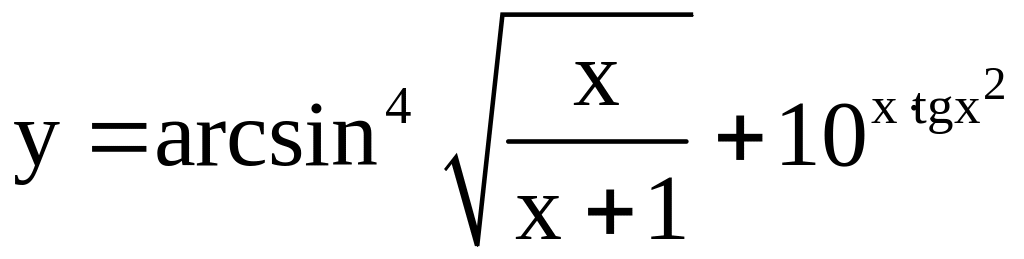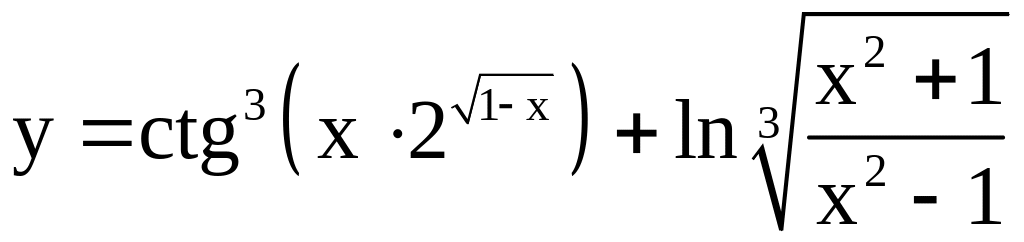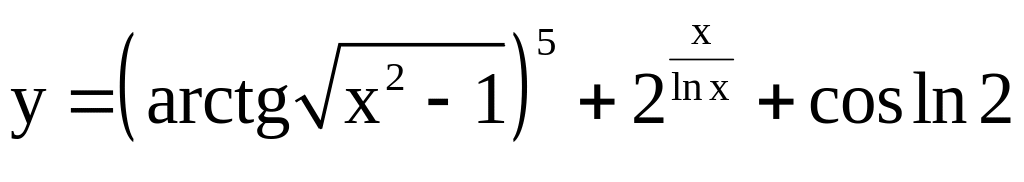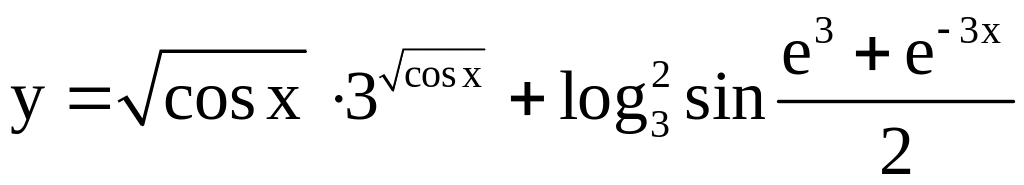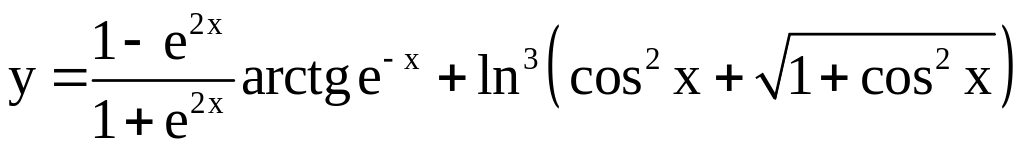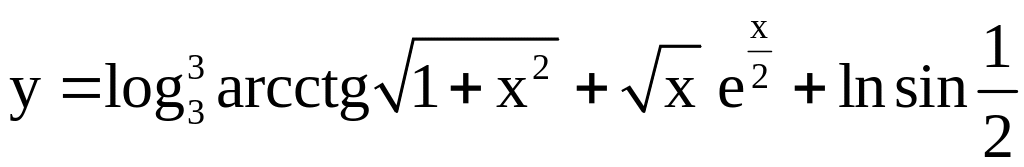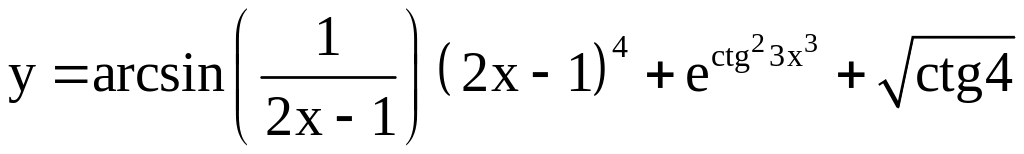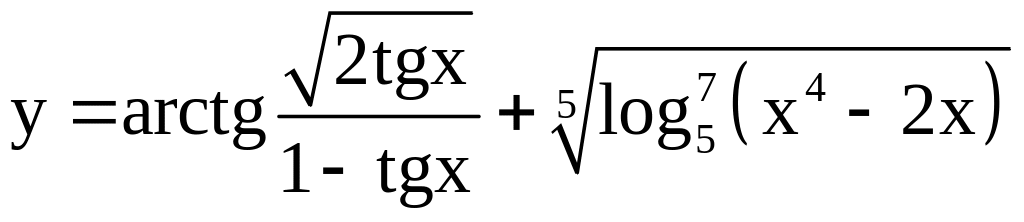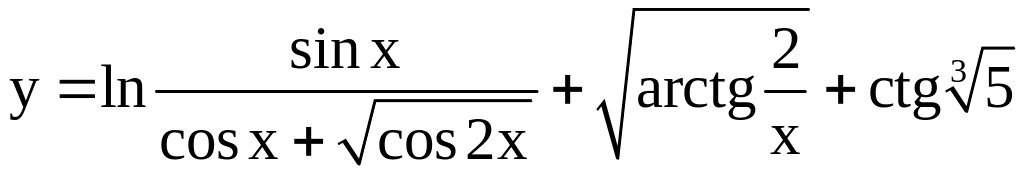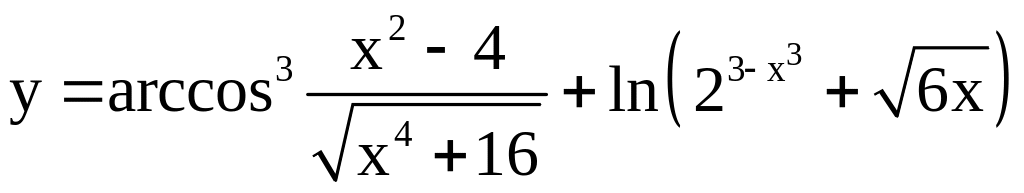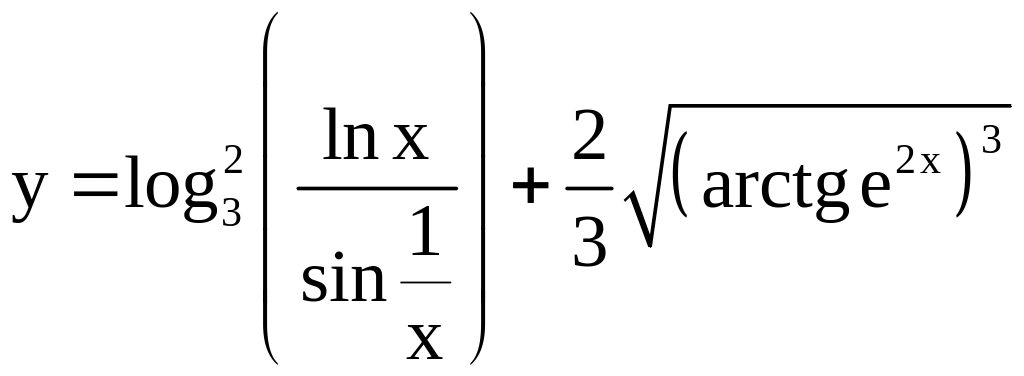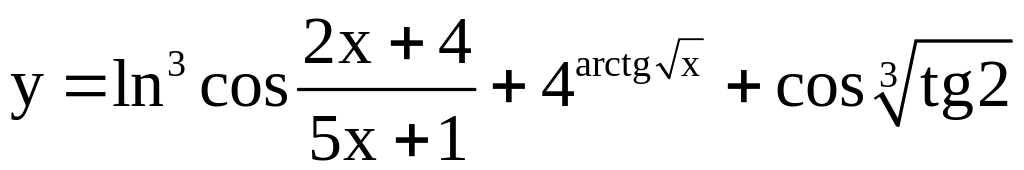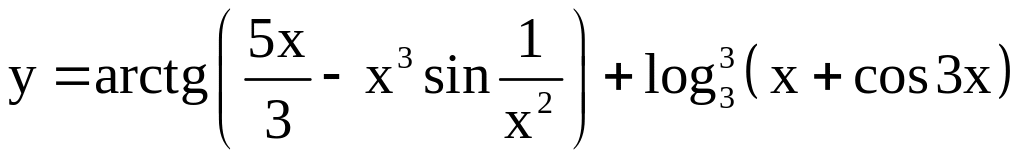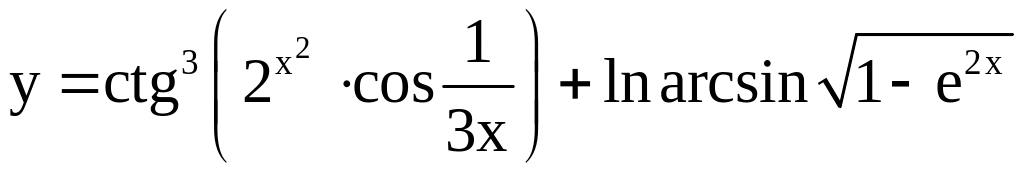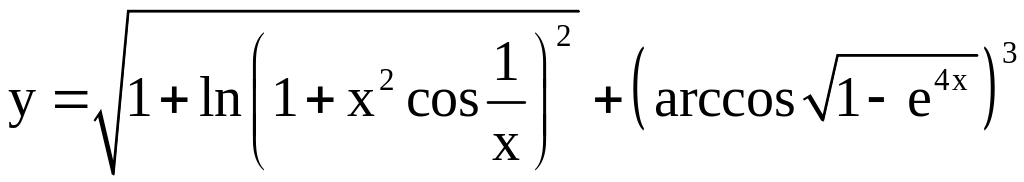Задание 5.4
Найдите дифференциал
.
1)
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
;
10)
;
11)
;
12)
;
13)
;
14)
;
15)
;
16)
;
17)
;
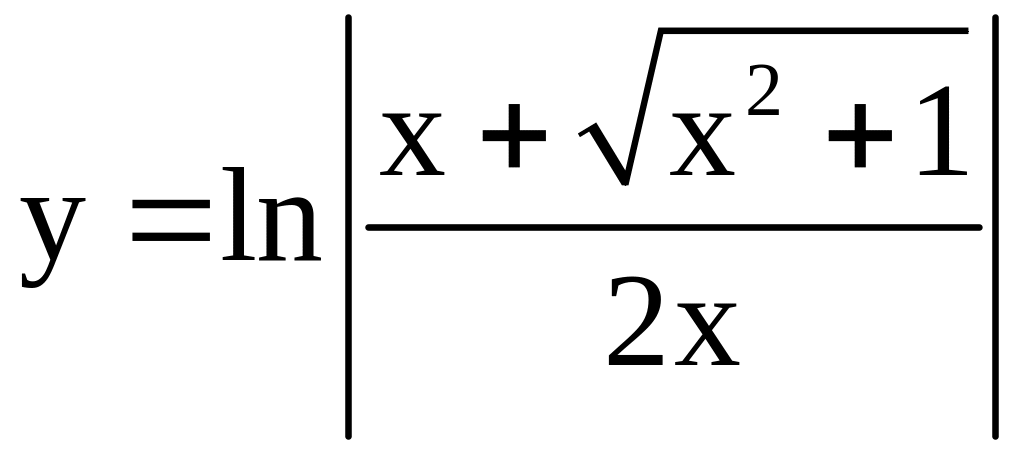18)
;
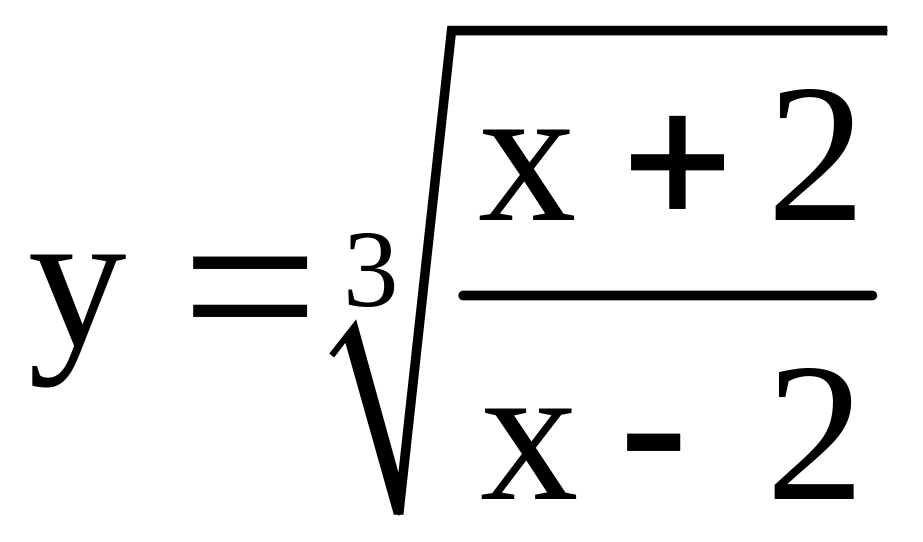19)
;
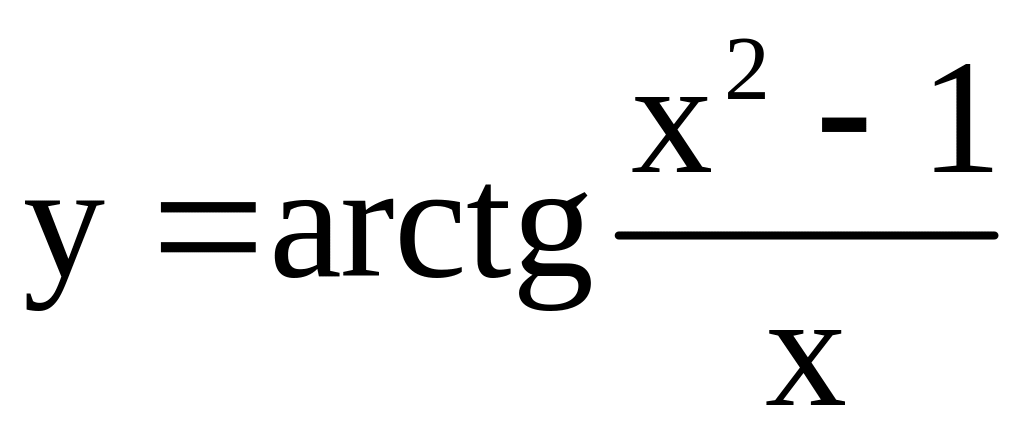20)
;
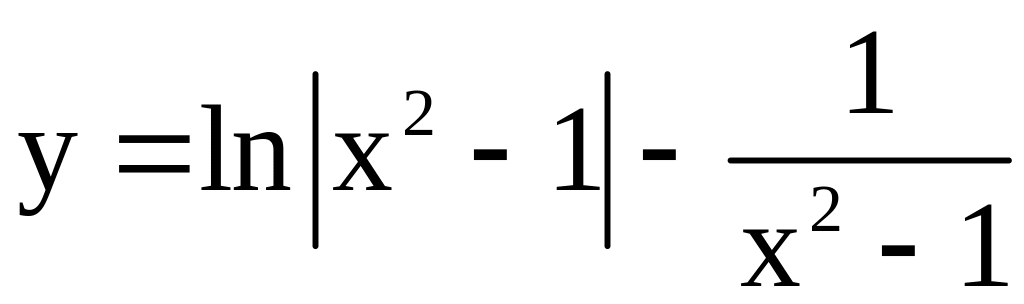21)
;
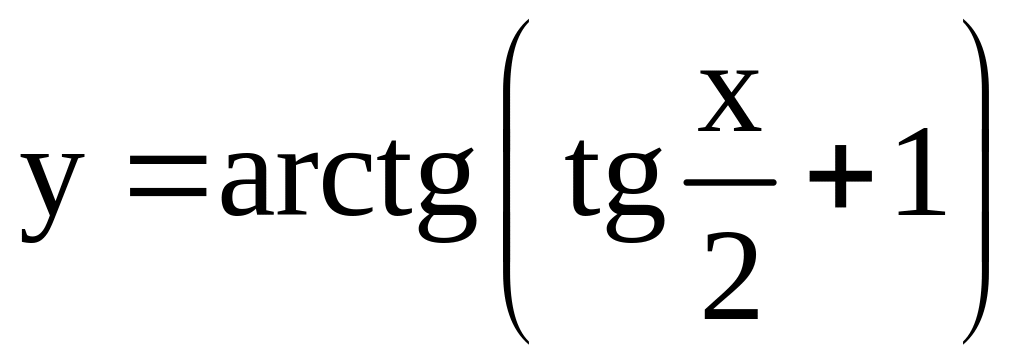22)
;
23)
;
24)
;
25)
;
26)
;
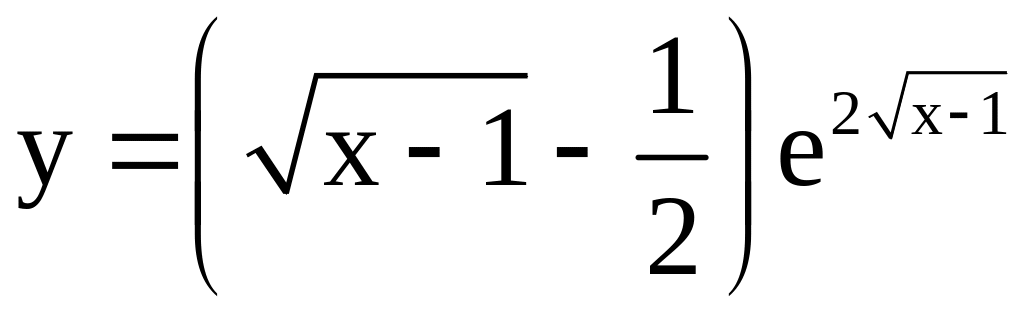27)
;
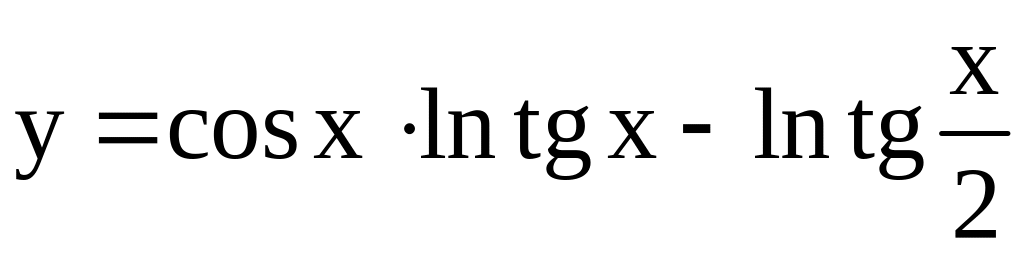28)
;
29)
;
30)
.
Задание 5.5
Найдите производную
1)
|
3)
|
2)
|
4)
|
5)
|
18)
|
6)
|
19)
|
7)
|
20)
|
8)
|
21)
|
9)
|
22)
|
10)
|
23)
|
11)
|
24)
|
12)
|
25)
|
13)
|
26)
|
14)
|
27)
|
15)
|
28)
|
16)
|
29)
|
17)
|
30)
|
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
.Задание 5.6
Найдите производную
1)
;
2)
;
3)
;
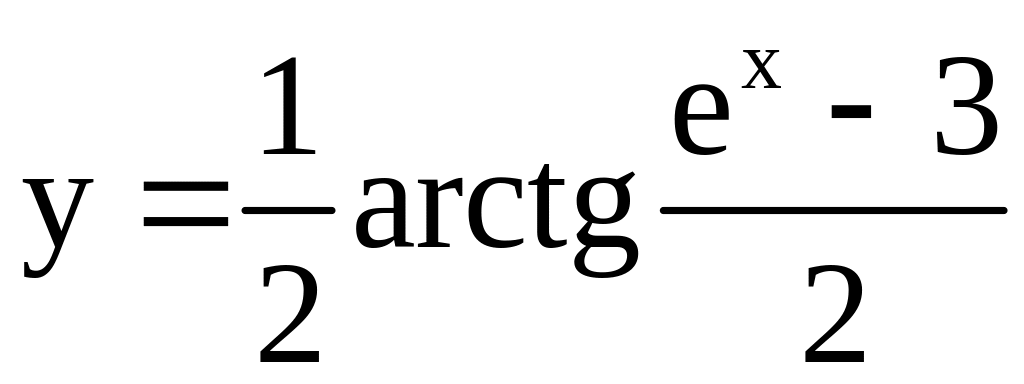4)
;
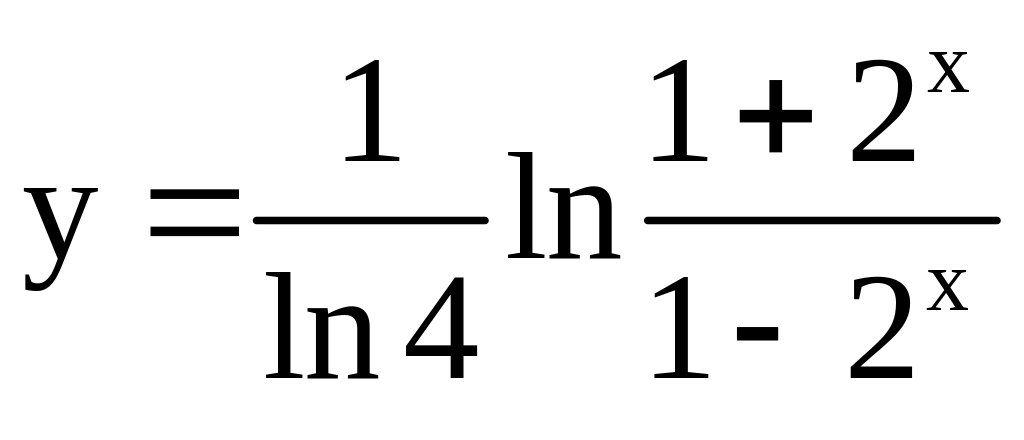5)
;
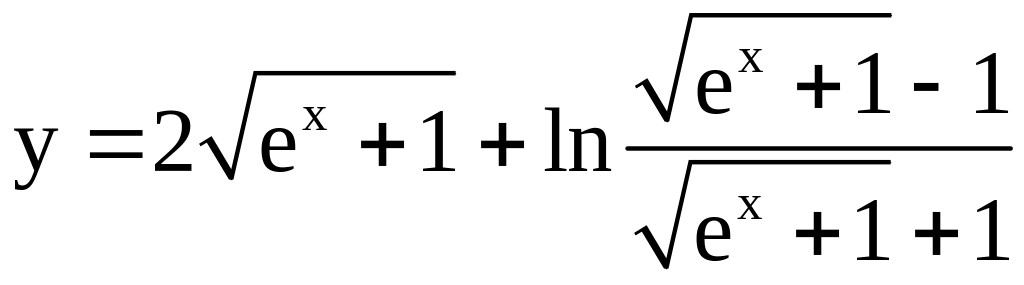6)
;
7)
;
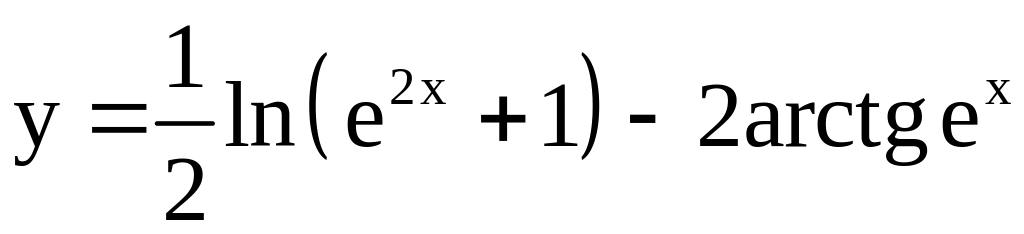8)
;
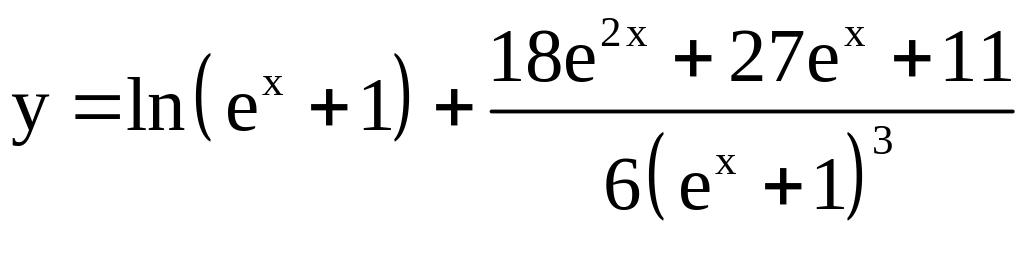9)
;
10)
;
11)
;
12)
;
13)
;
14)
;
15)
;
16)
;
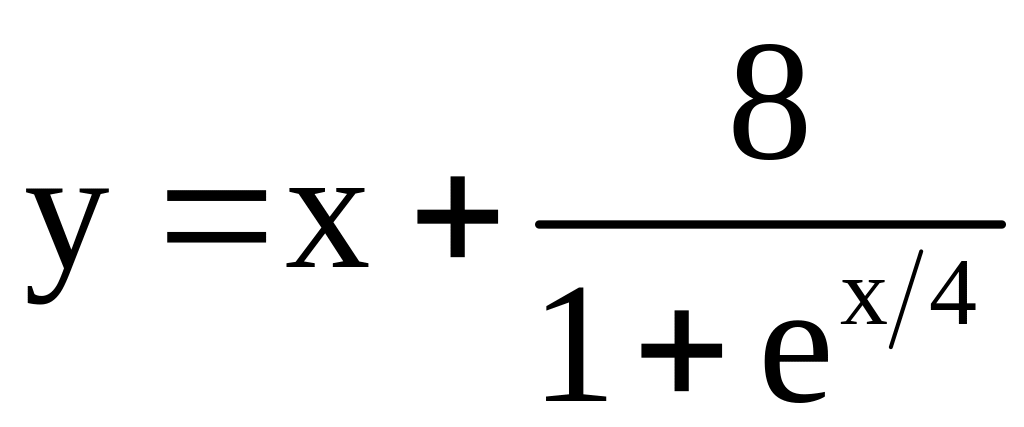17) ;
18)
;
19)
;
20)
;
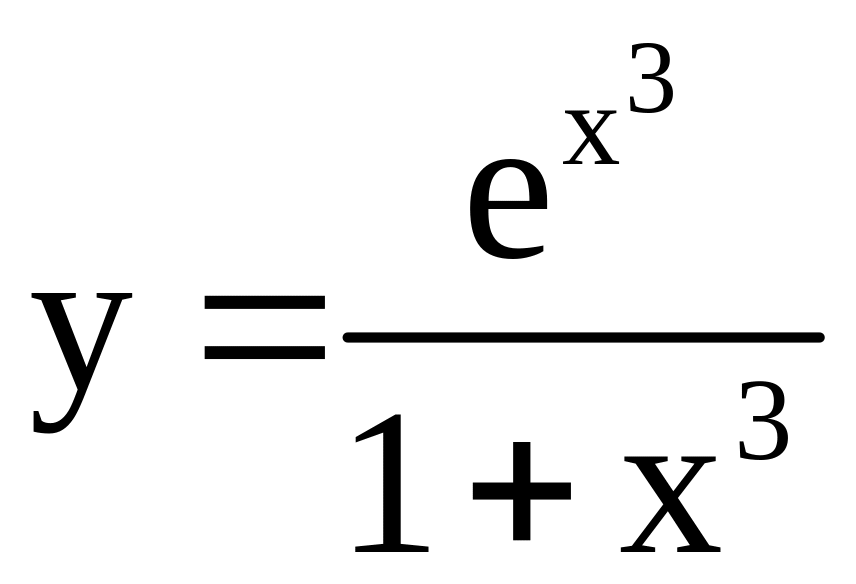21)
;
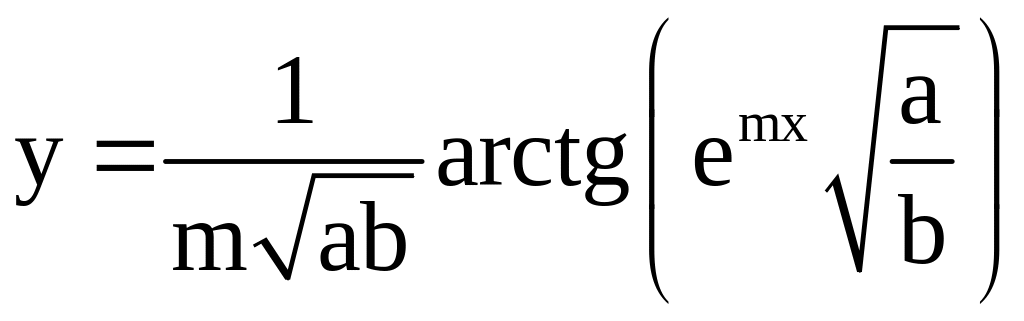22)
;
23)
;
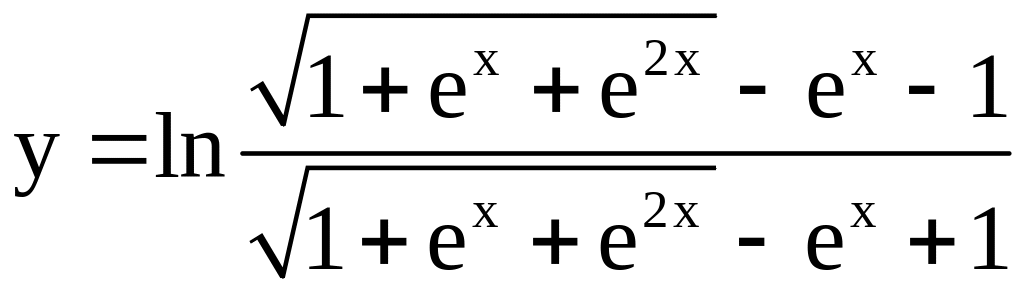24)
;
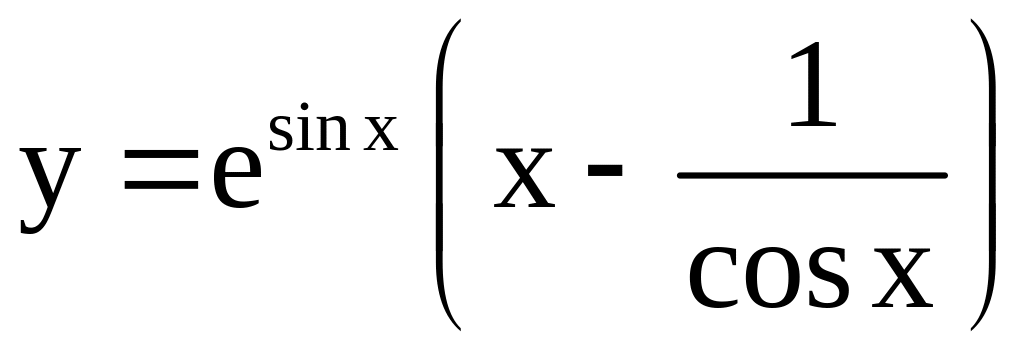25)
;
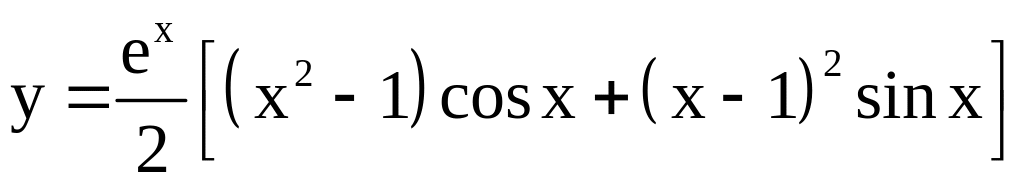26)
;
27)
;
28)
;
29)
;
30)
.
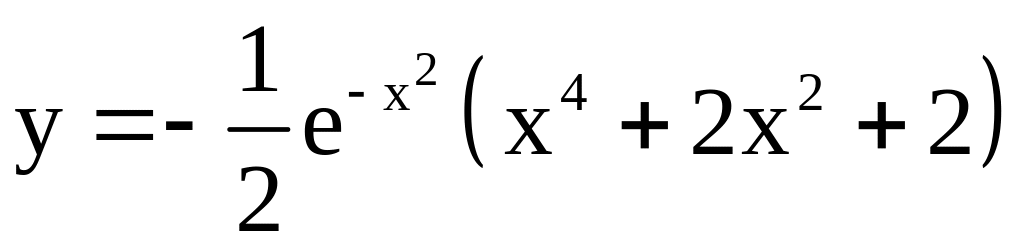
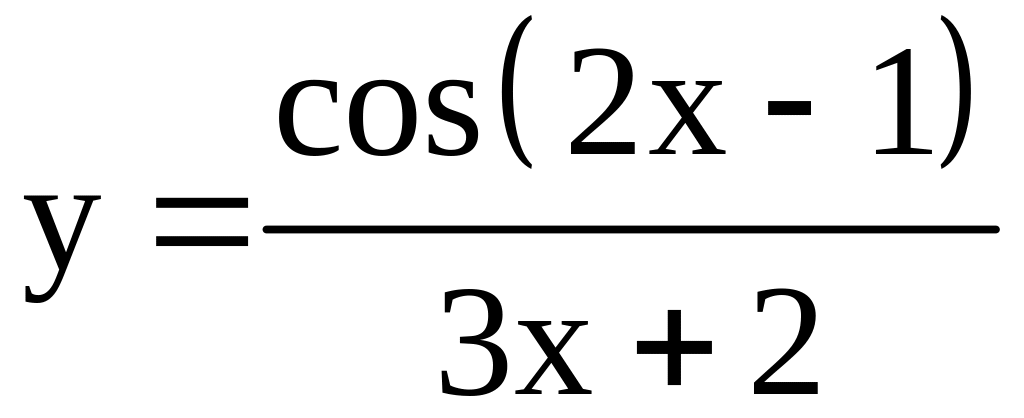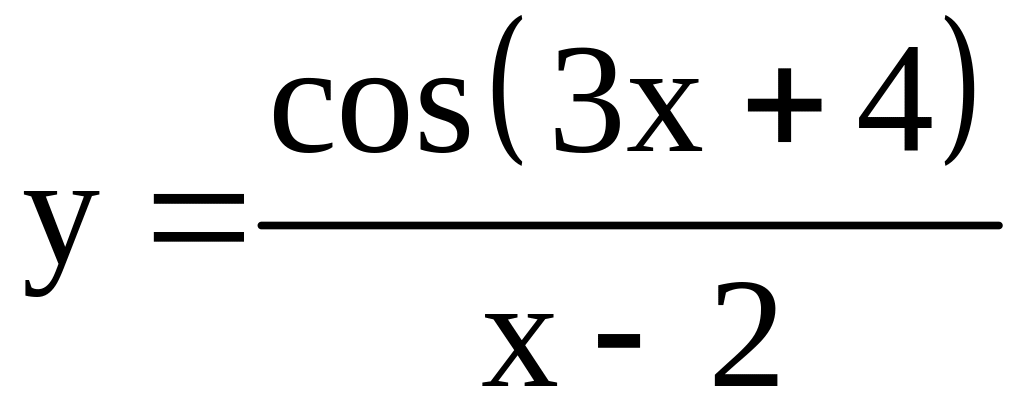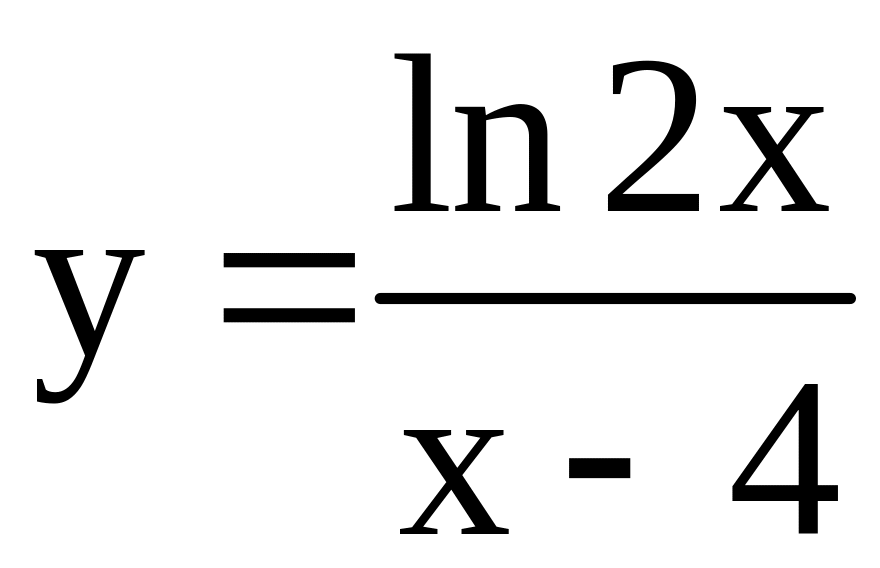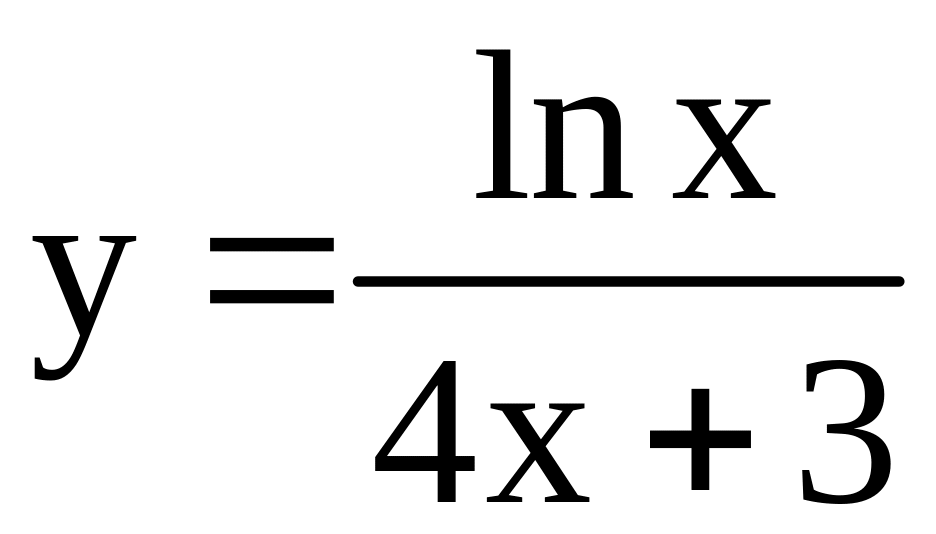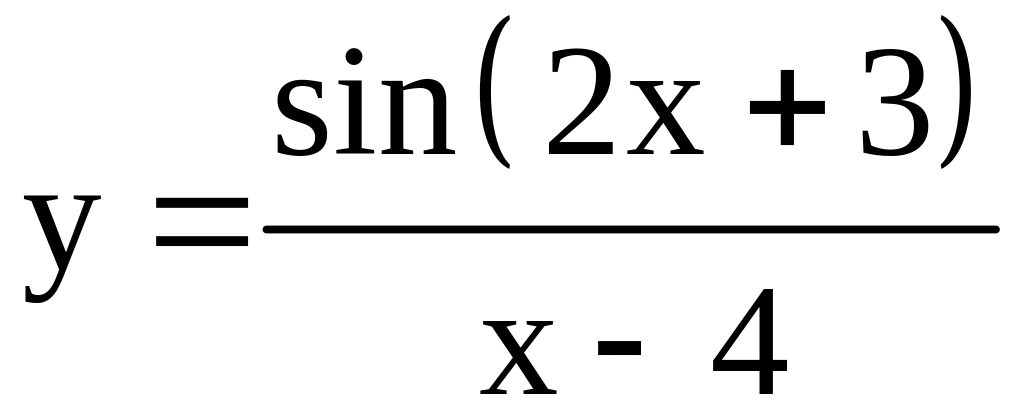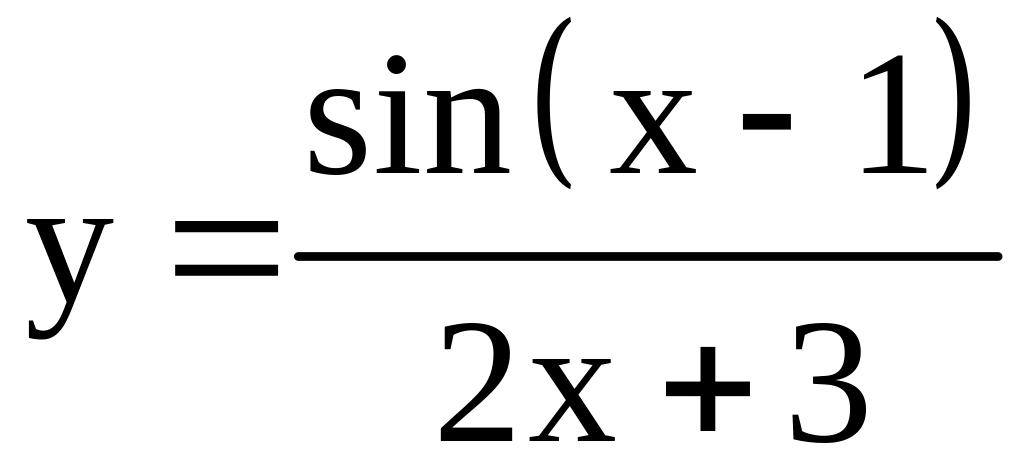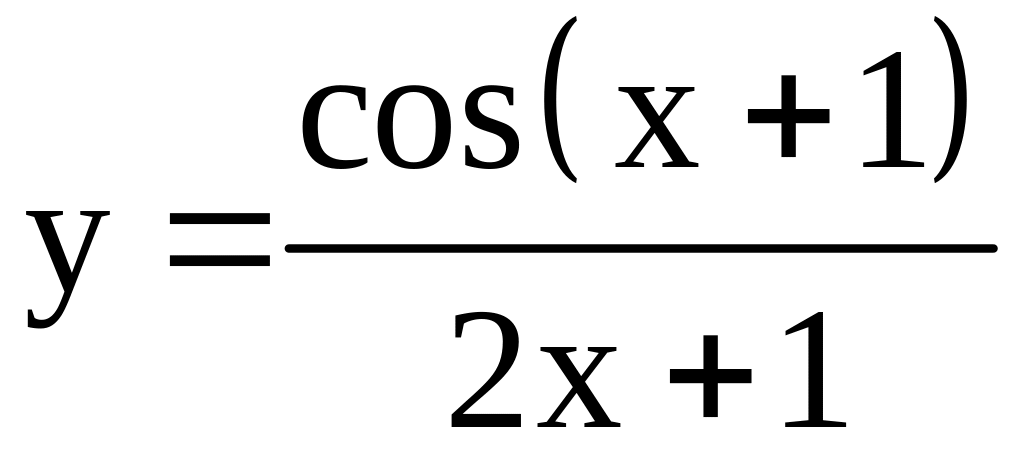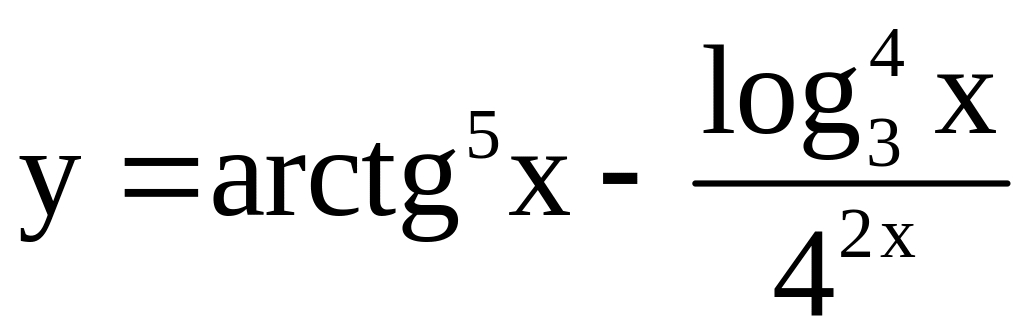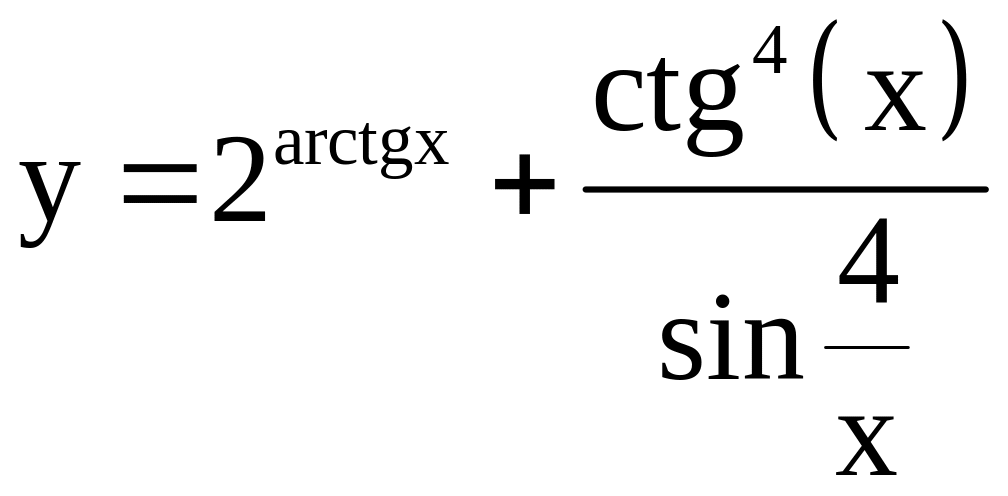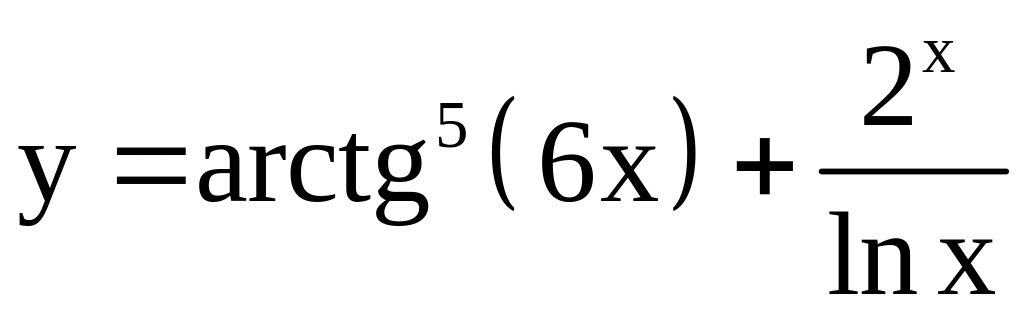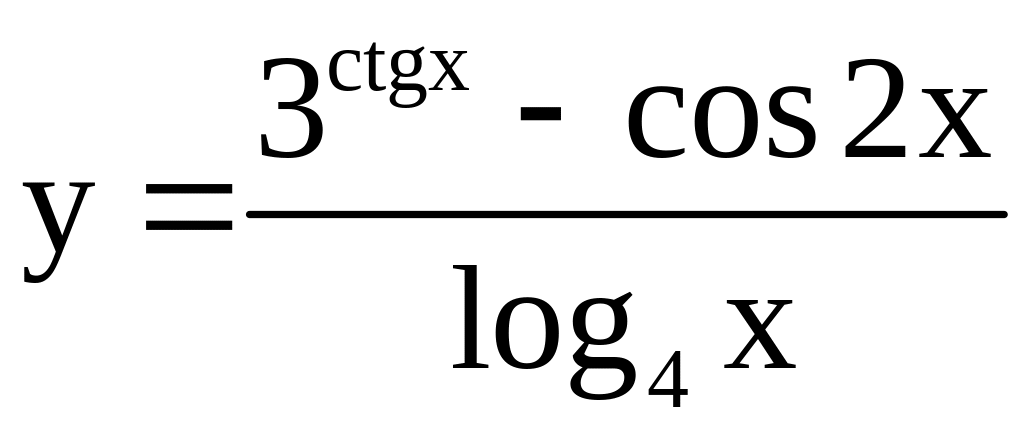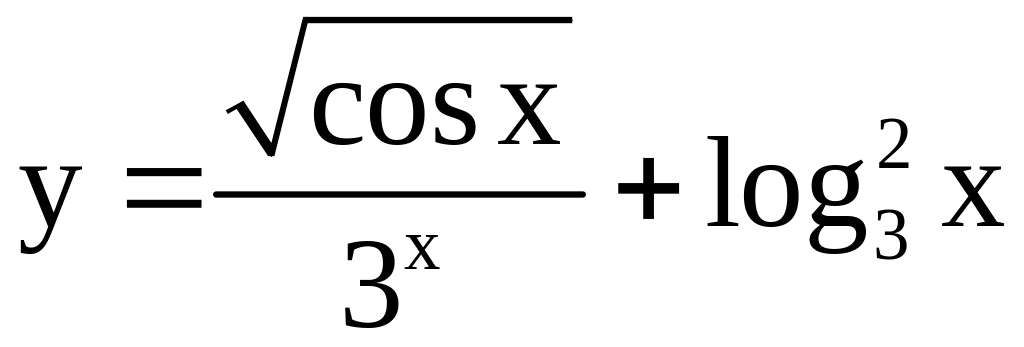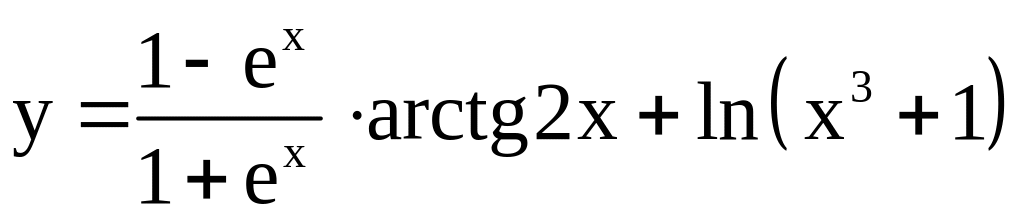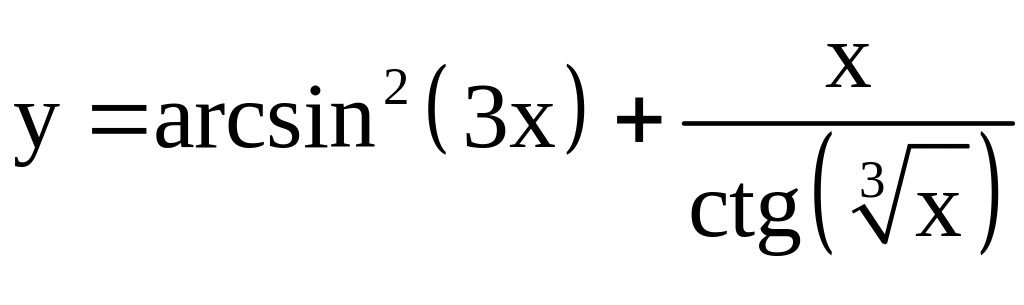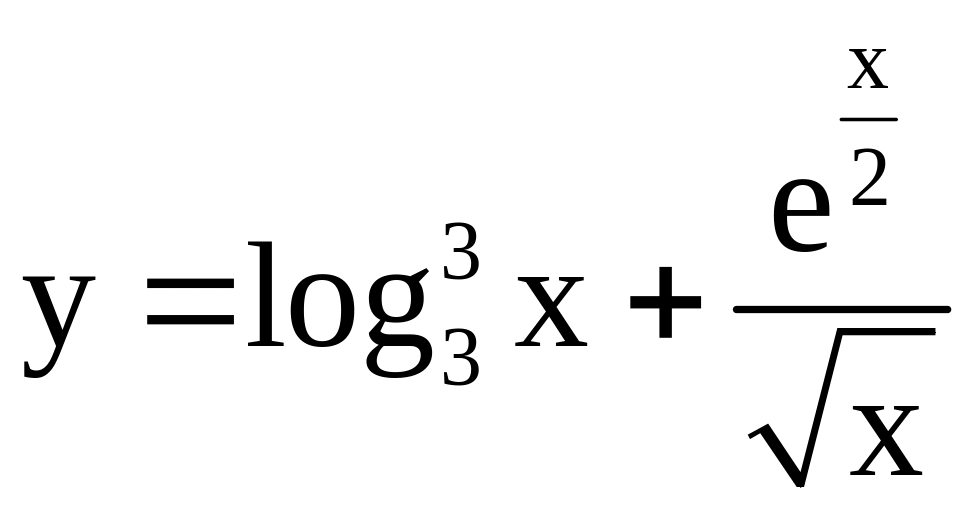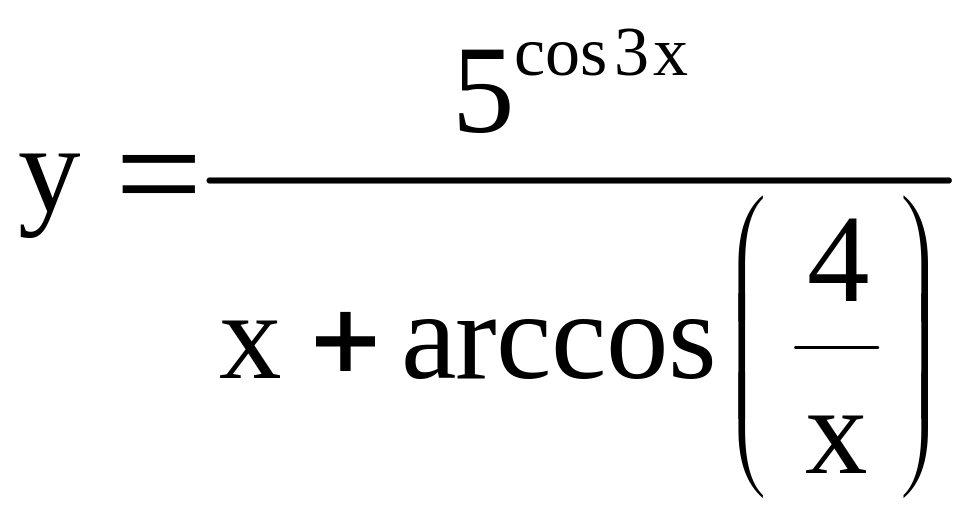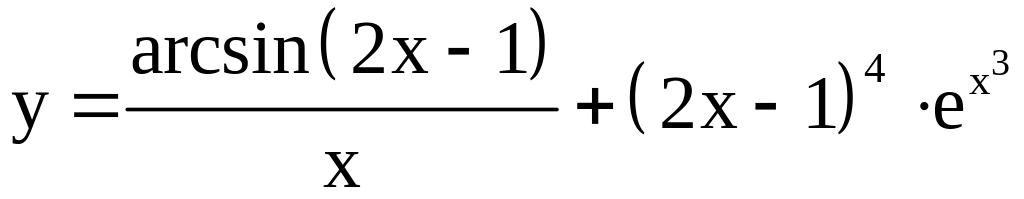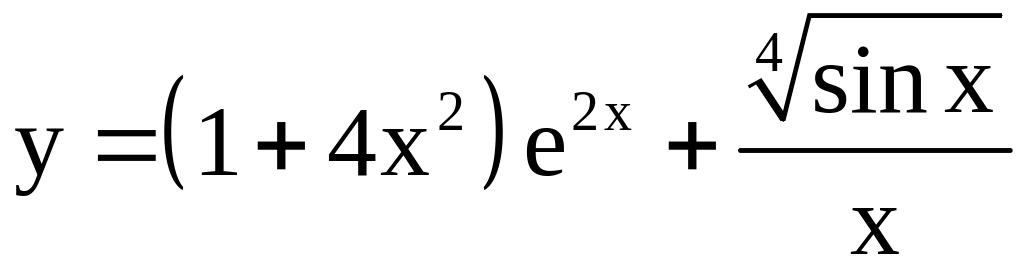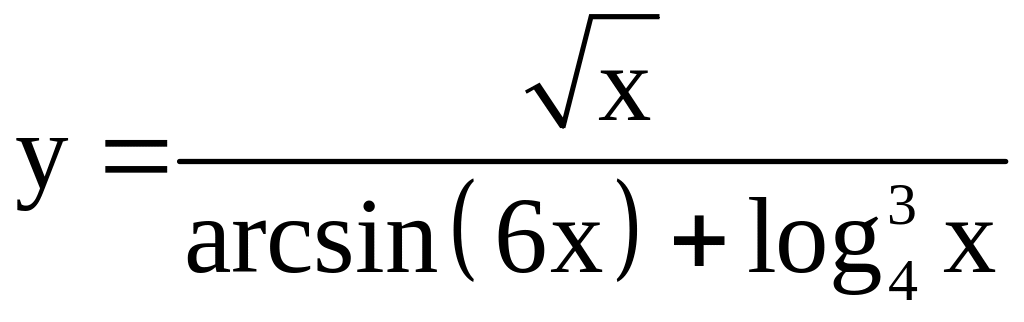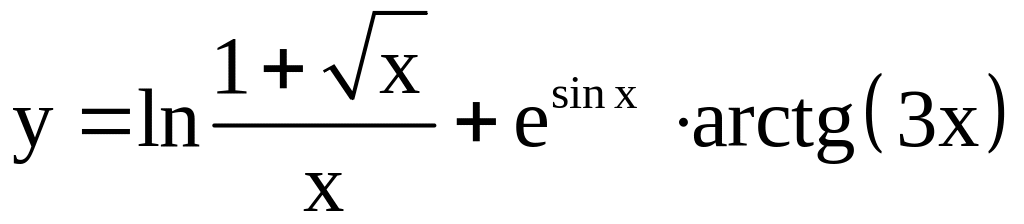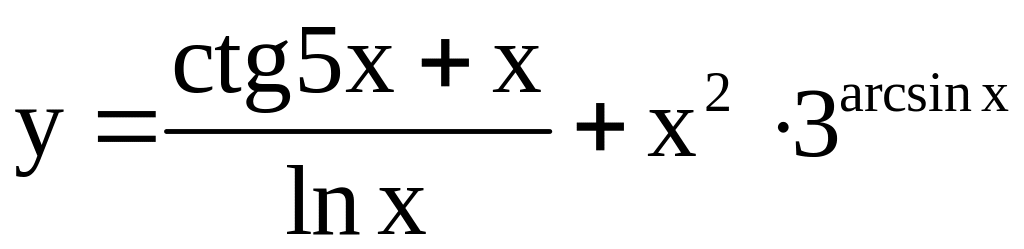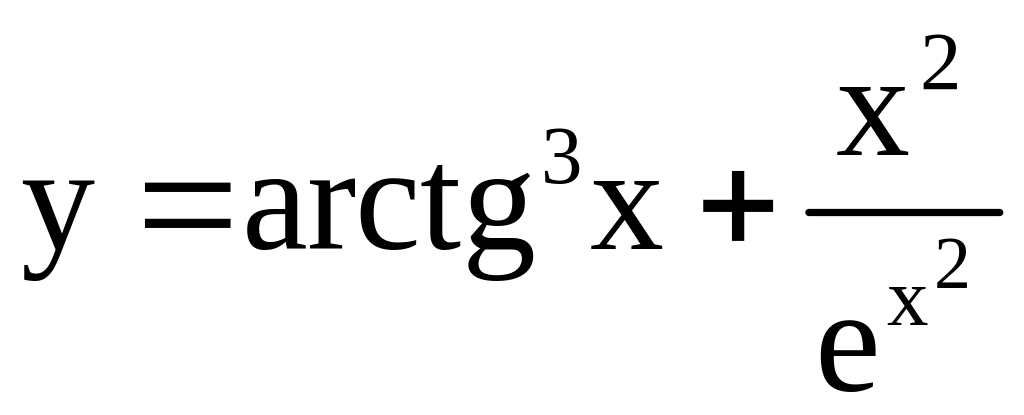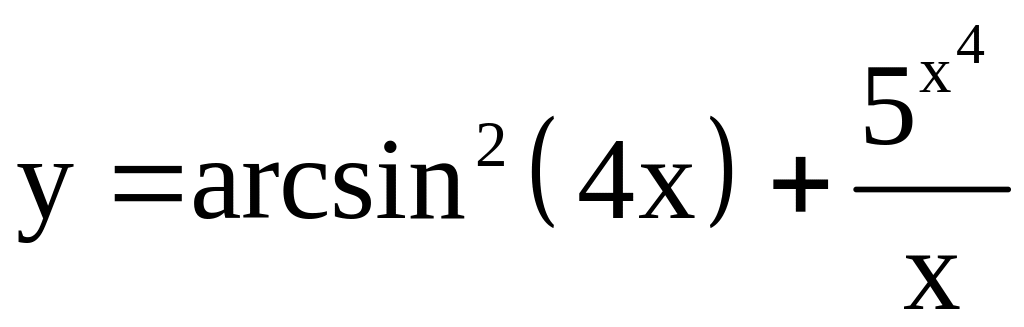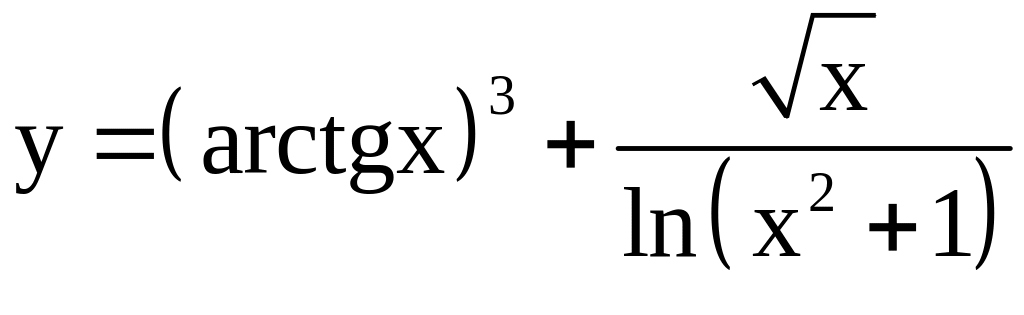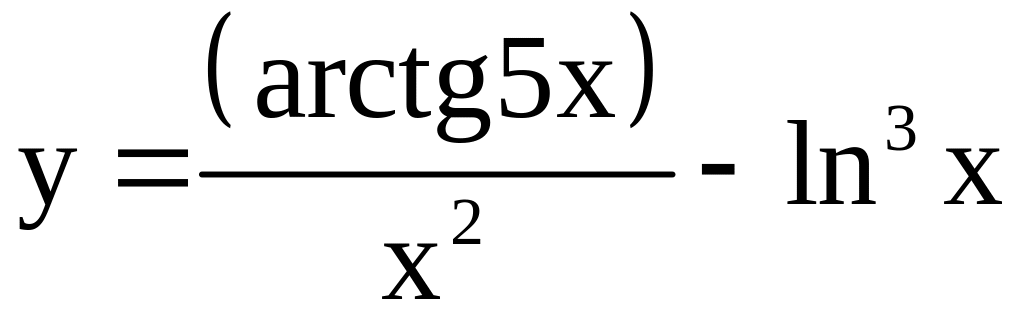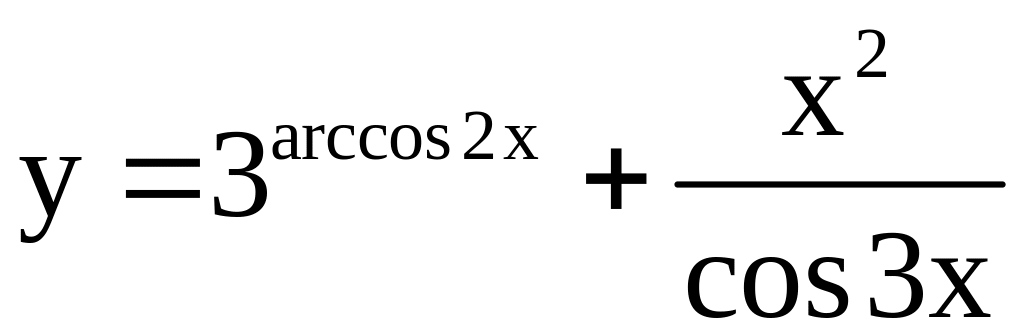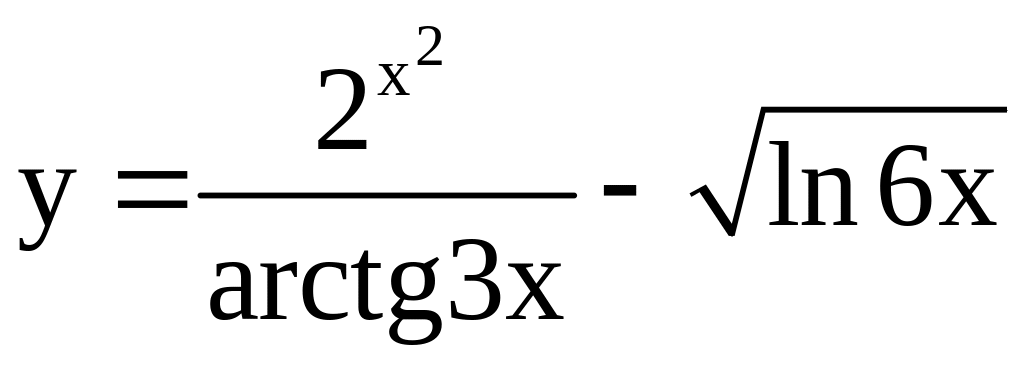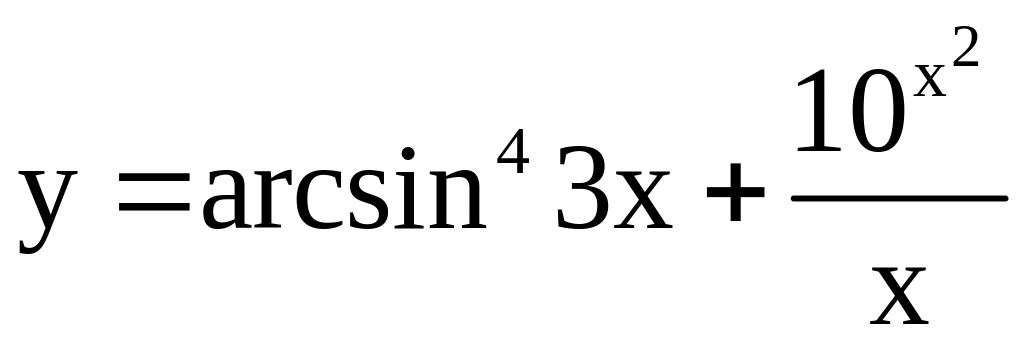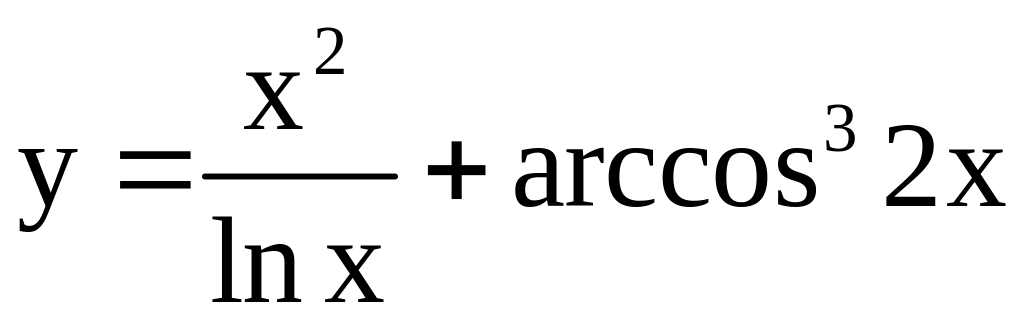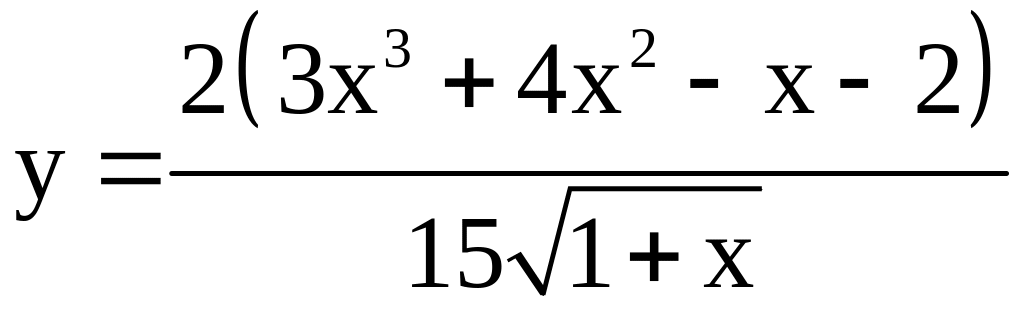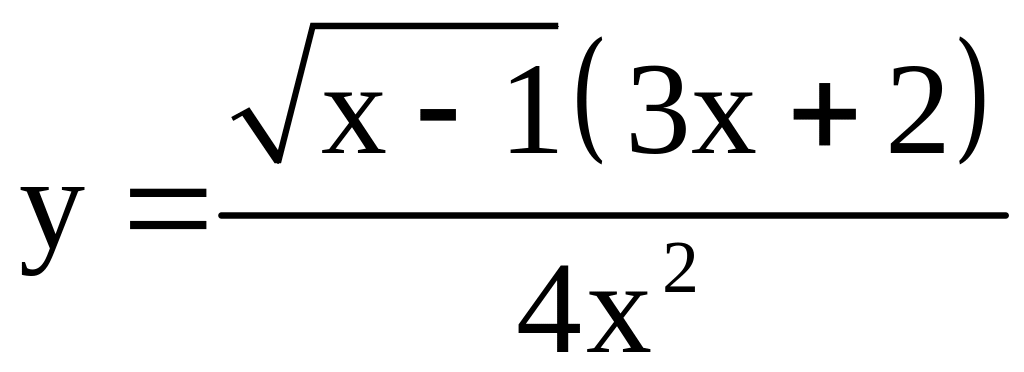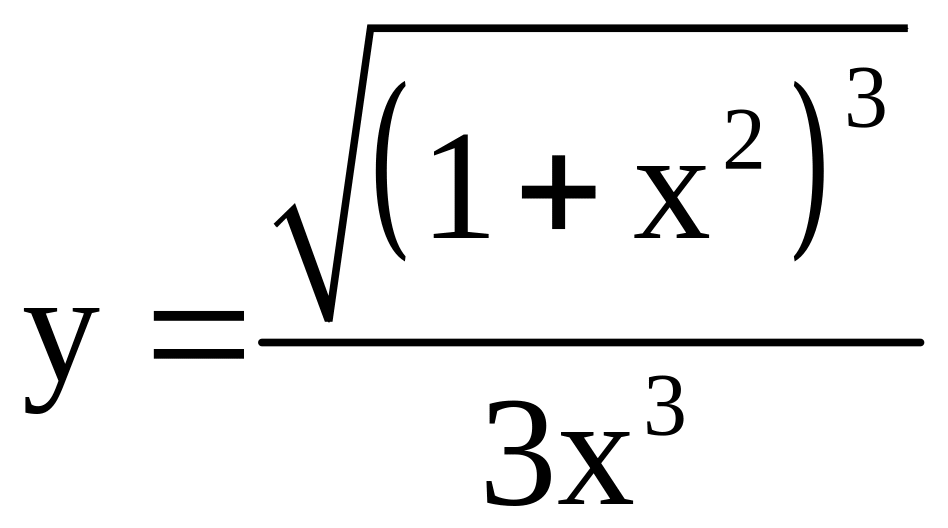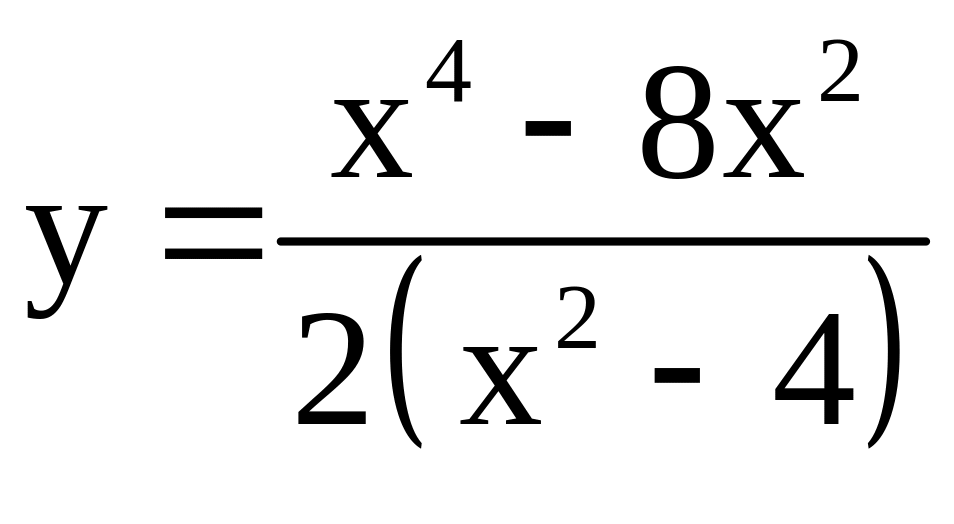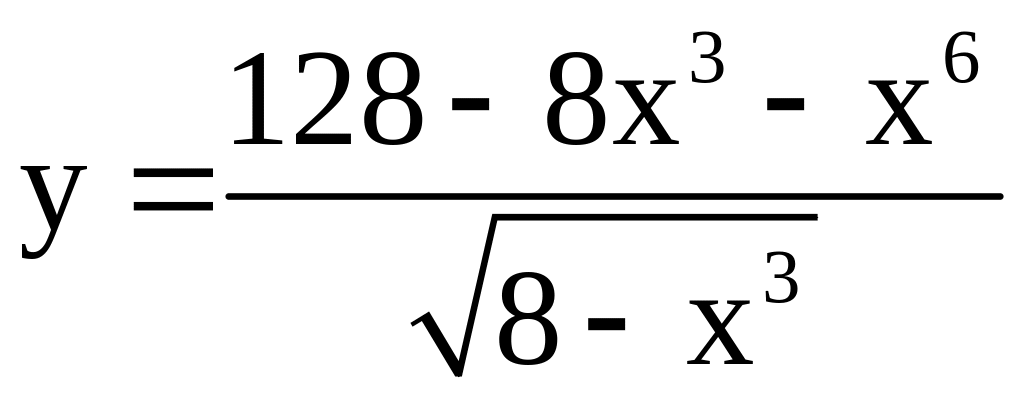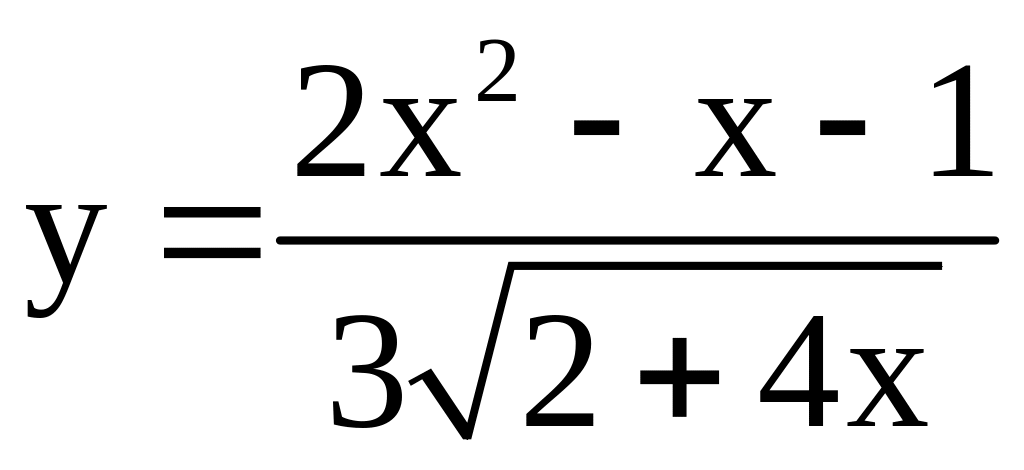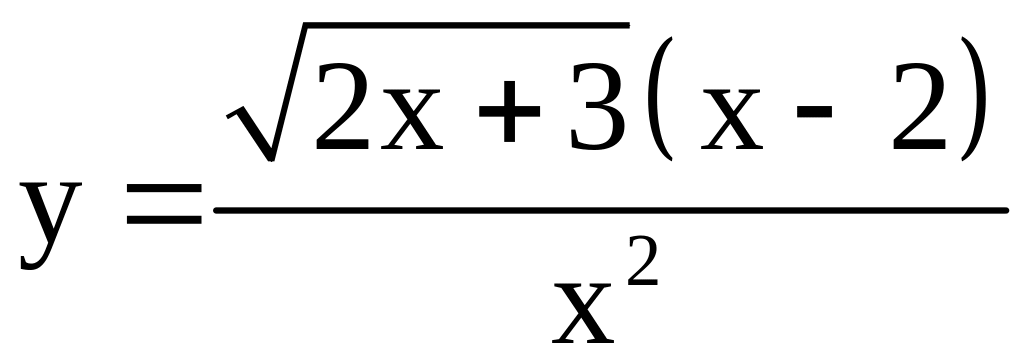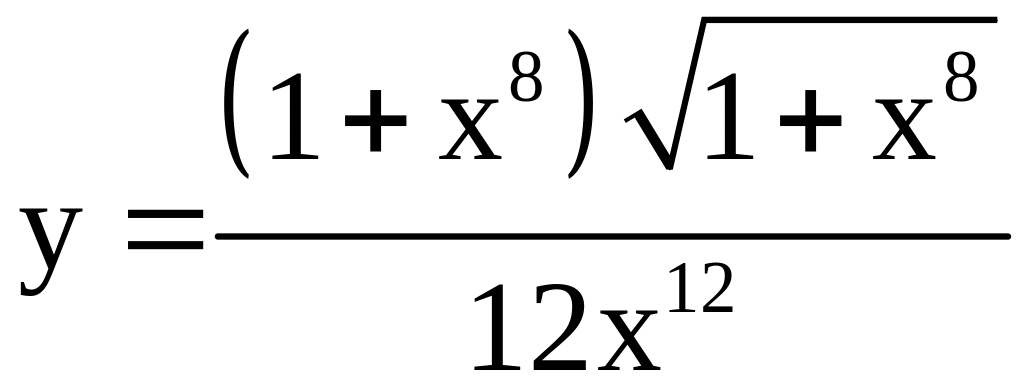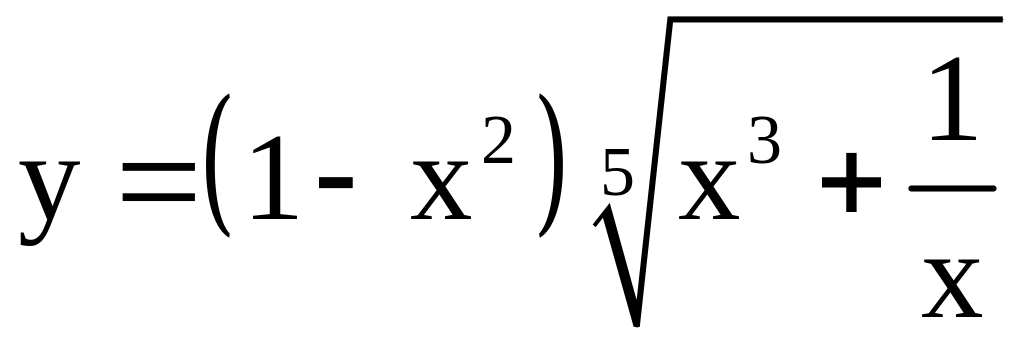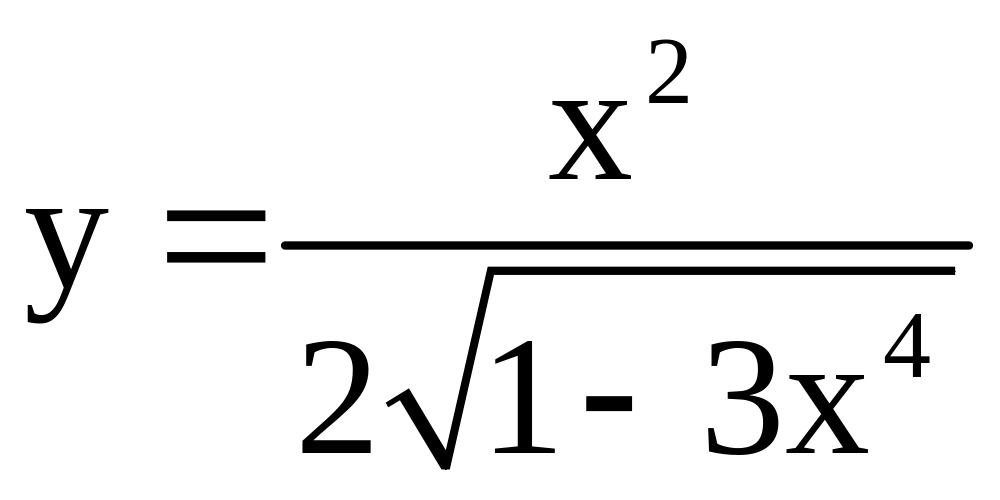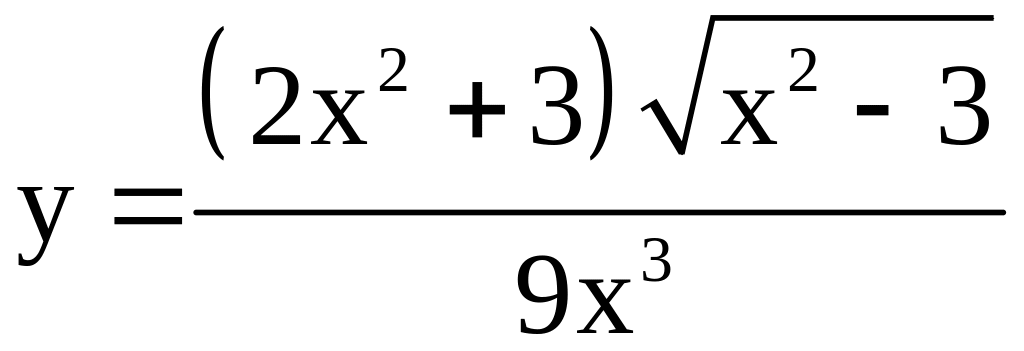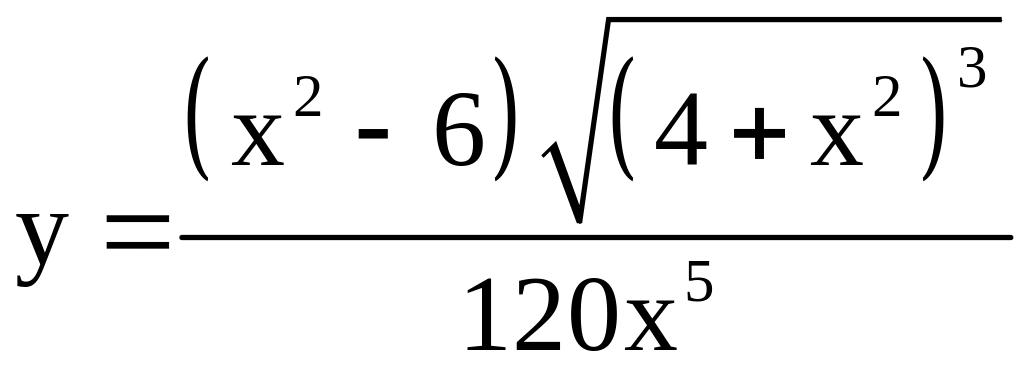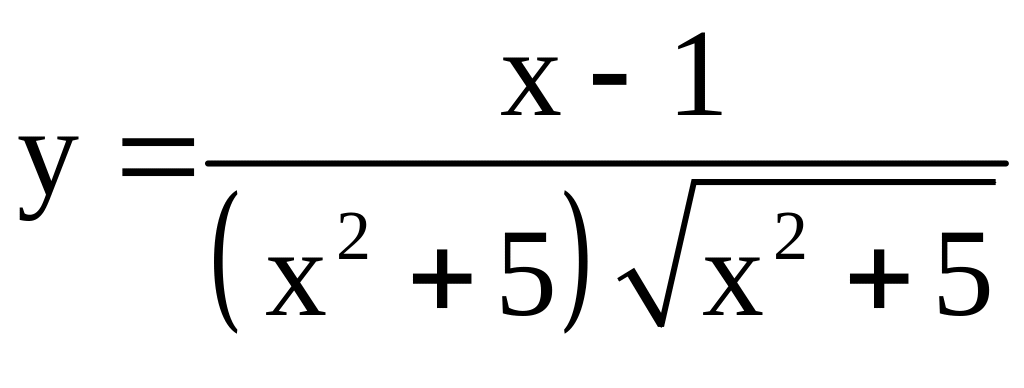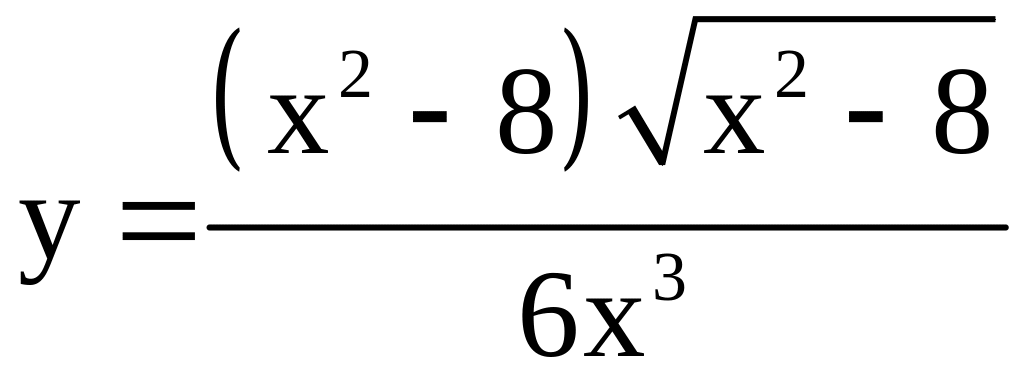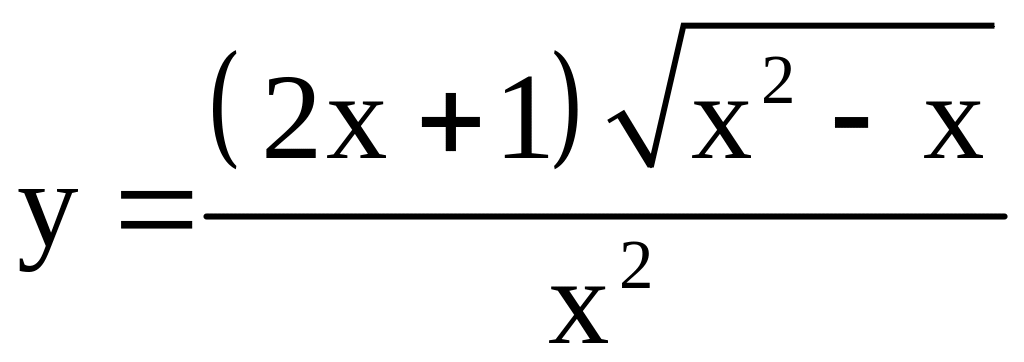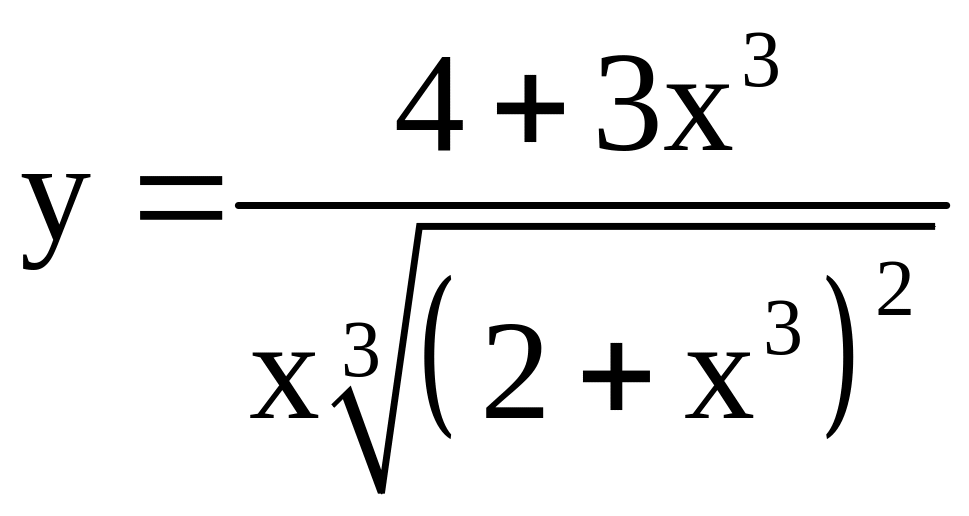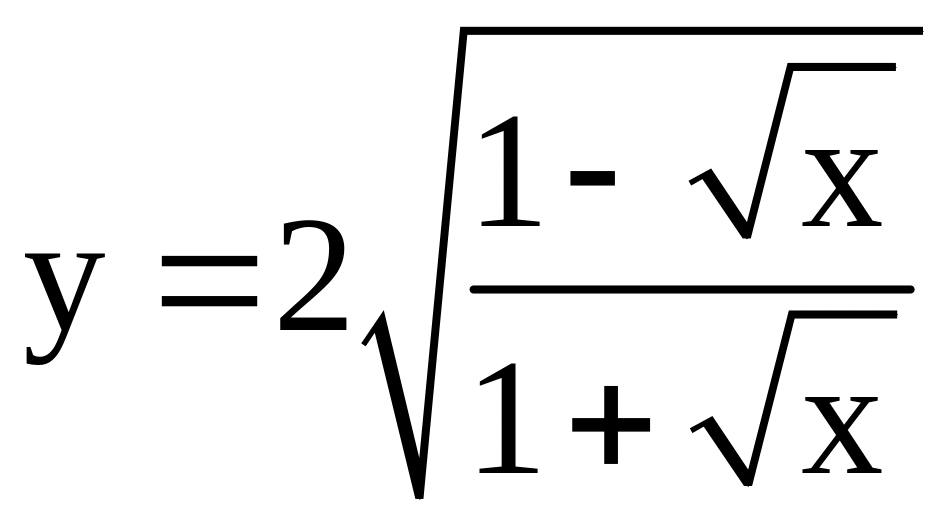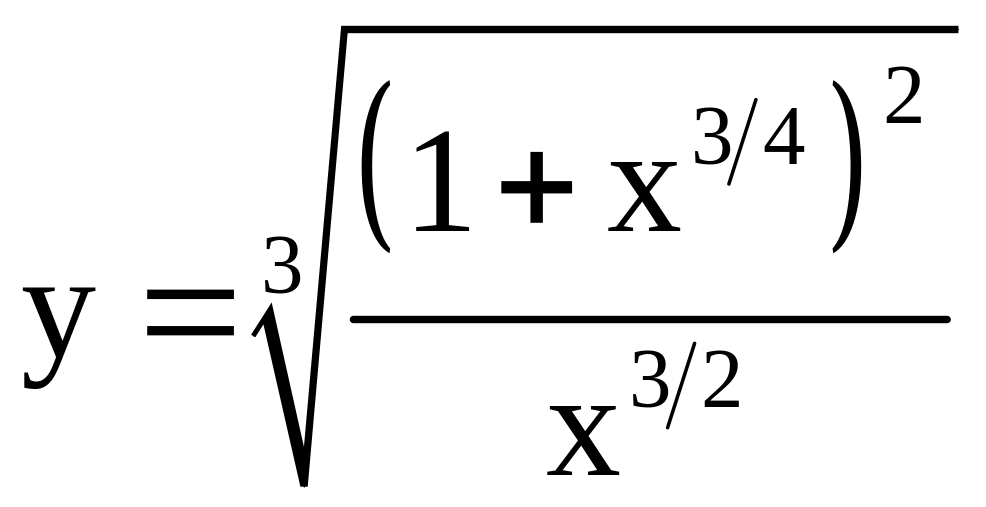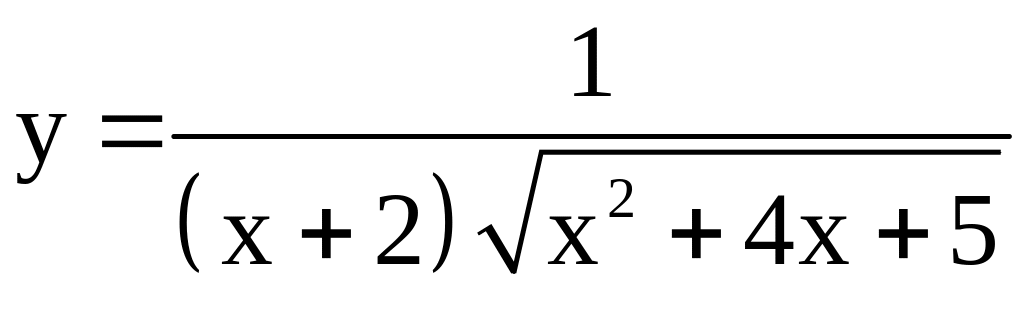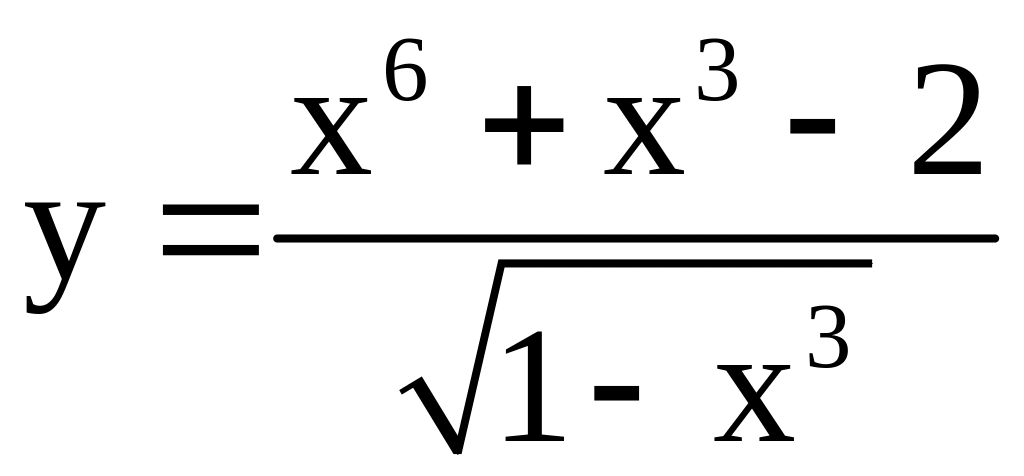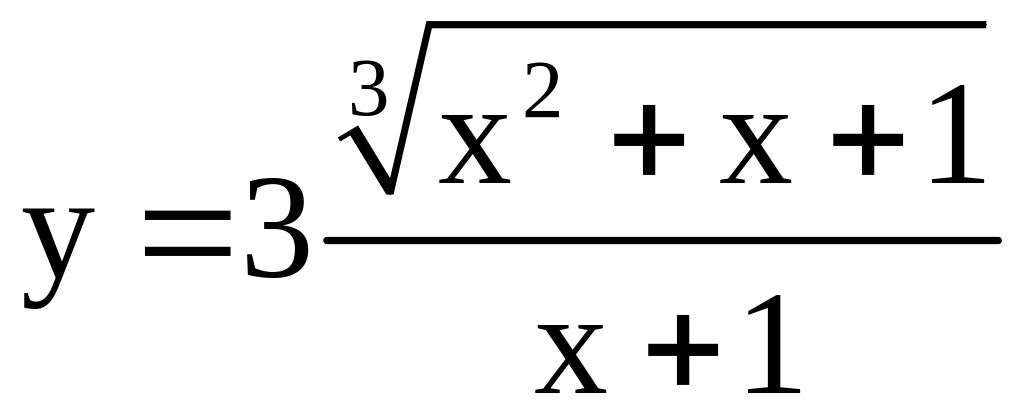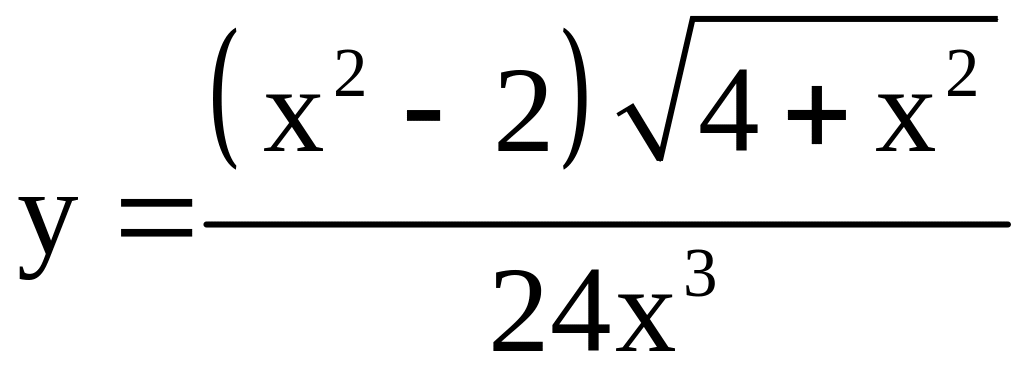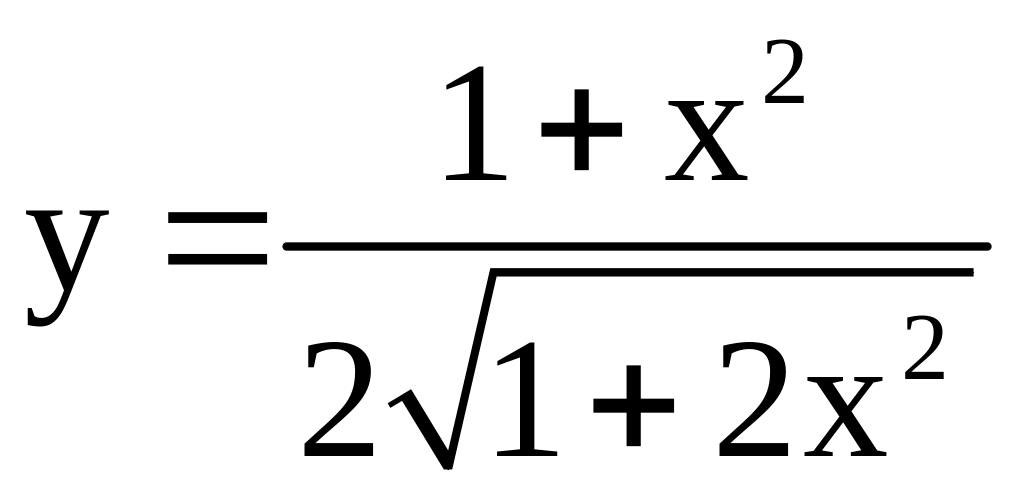