2.1.2. Расчет ящичных калибров

Коэффициент трения [2]

(2.22)

где средняя температура прокатки.

Средняя температура прокатки находится по формуле [2]

(2.23)

где t_H – температура начала прокатки, t_H=1200 ;

t_K – температура конца прокатки, t_K= .

Определим катающий диаметр по формуле [2]

(2.24)

где

Определим максимальное обжатие в 1 проходе [2]

(2.25)

где - катающий радиус

Катающий радиус мм находится по формуле [2]

(2.26)

Определим количество проходов по формуле [2]

(2.27)

где - высота заготовки, H= мм;

- ширина заготовки, B= мм;

- высота готового профиля, h = мм;

– ширина готового профиля, b = мм.

Полученное значение n округляем до большего целого числа.

Определим среднее обжатие [2]

(2.28)

Составляем предварительную схему обжатий.

Таблица 2.3 – Предварительная схема обжатий

Номер калибра	Ввр/Вд	Проход	Сечение HxB, мм	Абсолютн. обжатие Δh, мм	Относит. Обжатие ε,%	Уширение, мм
1		0к		-	-	-
		1
		2к
		3
		4к
2		5
		6к
3		7
		8к
4		9

Определим уширение по формуле [2]:

(2.29)

где - радиус валка, мм;

- обжатие, мм;

с – сторона квадрата, мм.

Пример:

, принимаем 10

, принимаем 10

, принимаем 15

Рассчитываем размеры калибров ( , , , S, ), мм [2]. Определяющими факторами являются минимальная высота и максимальные ширины раската в каждом калибре [2].

, мм (2.30)

, мм (2.31)

, мм (2.32)

, мм (2.33)

tgφ = (2.34)

Для 1 калибра:

Для 2 калибра:

Для 3 калибра:

Для 4 калибра:

И т д.

Найдем площадь , сечения в каждом проходе [2]

(2.35)

F₁ F₂ F₃ и т.д. в зависимости от числа проходов.

Определяем коэффициент вытяжки в каждом проходе [2]

(2.36)

- и т.д. в зависимости от количества проходов.

Найдем длину раската в каждом проходе [2]

(2.37)

- и т.д. в зависимости от количества проходов.

Составим таблицу калибровки для стали диаметром мм:

Таблица 2 – Калибровка круглой стали ø мм

№ кали-бра	Глубина вреза , мм	Про-ход	Сечение		Площадь F, мм2	Вытяжка λ	Обжатие ∆h, мм	Ушире-ние ∆b, мм	Длина L, мм
			H	B
		0к				-	-	-
1		1
		2к
		3
		4к
2		5
		6к
3		7
		8к
4		9к
5		10к
6		11

2. Квадратная сталь

2.1.1 Расчет калибровки квадратной стали

Размер стороны чистового квадратного калибра определяется с учетом использования минусового допуска = мм для компенсации износа валков, а также с учетом коэффициент линейного расширения металла.

При выборе коэффициента вытяжки в чистовом калибре λ_кв1 воспользуемся формулой [2]

, (2.38)

где c_кв1 – сторона чистового квадрата, с_кв1= мм.

Уширение в чистовом квадрате ∆b_кв1,мм, определяется по формуле [2]

, (2.39)

где D₁ – диаметр валков, мм, D₁= 850.

Высота предчистового ромба h₂, мм, находится по формуле [2]

(2.40)

Площадь сечения предчистового ромба будет находится по формуле [2]

, (2.41)

где F₁ – площадь чистового квадрата, которая находится по формуле:

_(2.42)

Ширину предчистового ромба b₂, мм, находится по формуле [2]

(2.43)

Обжатие в чистовом калибре по вершине калибра ∆h₁, мм, составит [2]

(2.44)

Угол захвата в чистовом калибре α₁ находится по формуле [2]

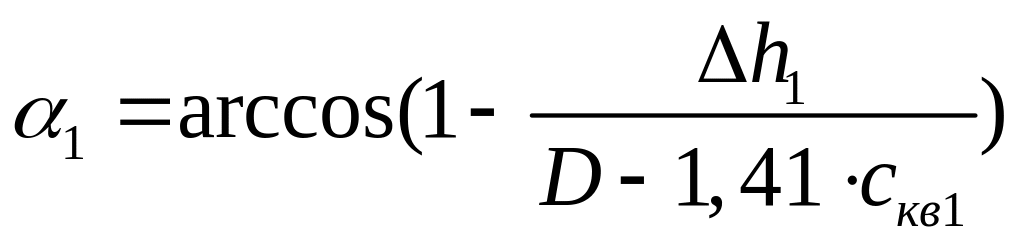(2.45)

Допускаемый угол захвата α_3max находится по формуле [2]

, (2.46)

где t – температура металла в чистовом калибре, ˚С, t= ;

ν – скорость прокатки в чистовом калибре, м/с , ν= .

_{Коэффициент вытяжки в предчистовом калибре λр2 составит} [2]

(2.47)

Площадь сечения предчистового квадрата F₃, мм², находится по формуле [2]

(2.48)

Сторону предчистового квадрата с₃, мм, находится по формуле [2]

(2.49)

Проверяем заполнение предчистового ромба 2, рассчитывая уширение ∆b_р2, мм, по следующей формуле [2]

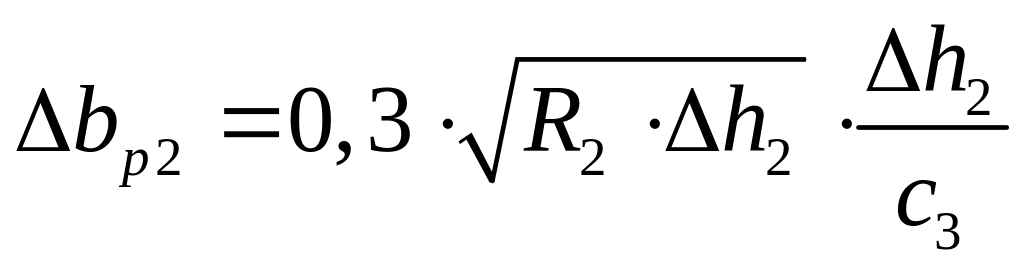, (2.50)

где R₂ – радиус валка по вершине калибра 2,мм;

∆h₂ - обжатие по вершине, мм.

Радиус валка R₂, мм, находится по формуле [2]

(2.51)

Обжатие по вершине ∆h₂ , мм, находится по формуле [2]

(2.52)

Ширина предчистового ромба b₂^’, мм, находится по формуле [2]

(2.53)

Производим корректировку размера предчистового квадрата, мм [2]

, (2.54)

где k₂ – поправочный коэффициент.

Поправочный коэффициент k₂ находится по формуле [2]

k₂= (2.55)

Пересчитываем величину уширения ∆b_р2, мм, и обжатия ∆h₂, мм, используя следующие формулы [2]

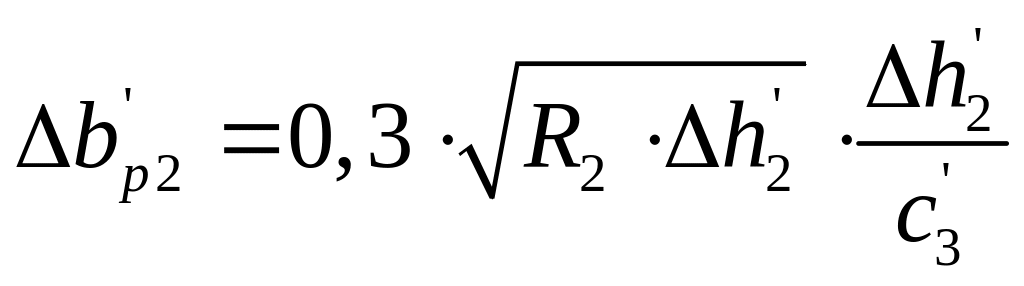(2.56)

(2.57)

Теперь ширина ромба b₂^’, мм, будет равна [2]

(2.58)

Угол захвата в предчистовом калибре α₂ составит [2]

(2.59)

Допускаемый угол захвата в калибре 2 [2]

(2.60)

, м/с (2.61)

Уточняем площадь сечения предчистового квадрата 3 и коэффициента вытяжки в предчистовом ромбе2 [2]

(2.62)

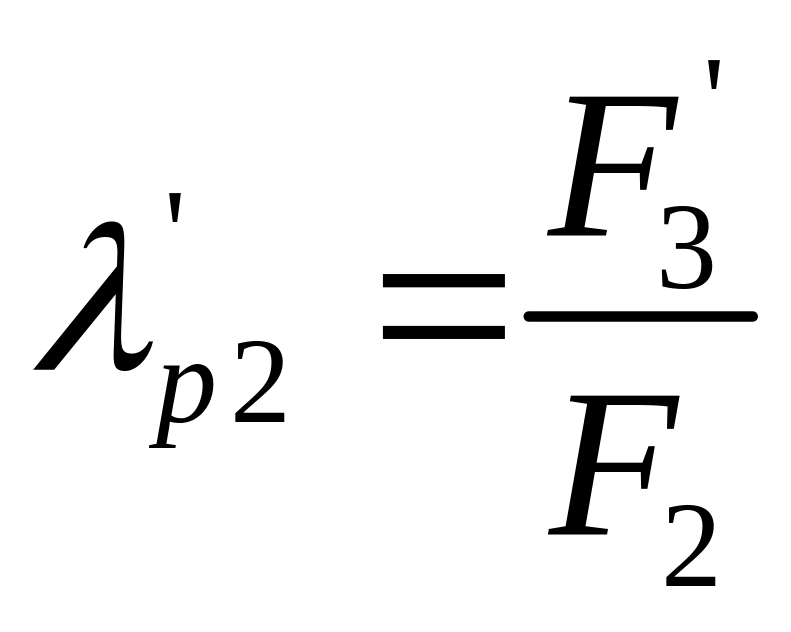(2.63)

2.1.2. Расчет ящичных калибров

Расчет ящичных калибров производится по тем же формулам, что и для круглой стали.

2.2 Расчет усилия прокатки

Рассчитываем усилие прокатки в первом проходе P,кН, по формуле [3]

(2.64)

где р_ср - среднее контактное давление, МПа;

B_cр - средняя ширина очага деформации, мм;

l_d - длина очага деформации.

Средняя ширина очага деформации , мм, находится по формуле [3]

(2.65 )

где В₀ – начальная ширина заготовки, В₀ = мм;

В₁ – конечная ширина заготовки в первом проходе, В₁ = мм.

Определяем длину очага деформации , мм [3]

( 2.66)

где R_k – рабочий радиус, мм;

- величина обжатия в первом проходе,мм, = .

Определяем катающий радиус R_k , мм, по формуле [3]

(2.67)

где D_k – катающий диаметр, мм.

Определяем катающий диаметр D_k , мм, по формуле [3]

(2.68)

где D_б – диаметр бочки, мм;

h_вр. – высота вреза в первом калибре, мм;

– зазор между буртами валков, = мм.

Определяем среднее контактное давление р_ср, МПа [3]:

( 2.69)

где - коэффициент, учитывающий ширину раската, , принимаю = 1;

- коэффициент, зависящий от очага деформации,

- коэффициент, учитывающий влияние внешних зон по отношению к геометрическому очагу деформации;

- сопротивление деформации, зависящее от марки стали, температуры прокатки и скорости деформации, Мпа.

При следует [3]:

(2.70)

Определяем среднюю высоту , мм [3]

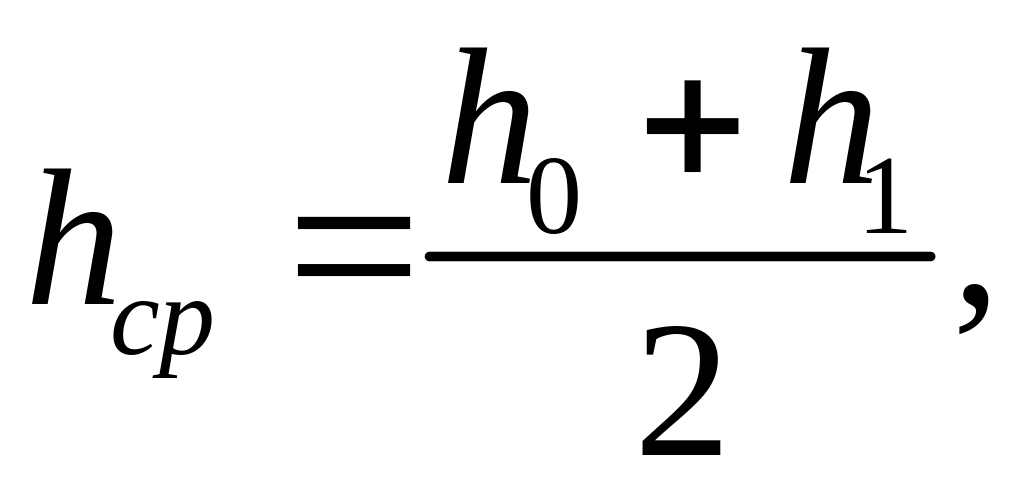(2.71)

где - начальная высота в первом проходе, мм, = ;

- конечная высота в первом проходе, мм, = .

Коэффициент определяем по формуле [3]:

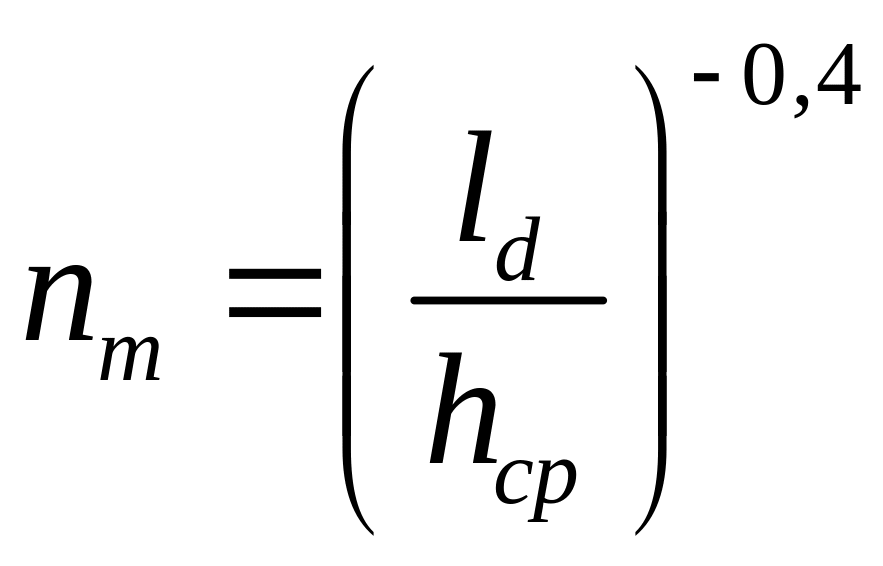(2.72)

Сопротивление деформации определяем по формуле [3]

(2.73)

где - базисное сопротивление деформации, = МПа;

- температурный коэффициент;

и - коэффициенты, учитывающие степень и скорость деформации соответственно.

Определяем температурный коэффициент [3]:

(2.74)

где - температура прокатки в первом проходе, = .

Для определения необходимо знать значение относительной деформации , %, которое определяется по формуле [3]:

(2.75)

Если , то (2.76)

Если , то (2.77)

Коэффициент определяем по формуле [3]:

( 2.78)

где – скоростной коэффициент.

Скоростной коэффициент определяем по формуле [3]

( 2.79)

где V – скорость прокатки, V= м/с.

Определяем среднее контактное давление , МПа:

Определяем усилие прокатки P, кН:

2.3 Расчет прокатного валка на прочность

2.3.1 Расчет бочки валка

Рассчитываем бочку валка. При расчете необходимо просчитать изгибающий момент , кН·м, действующий при прокатке. Он вычисляется по формуле [4]

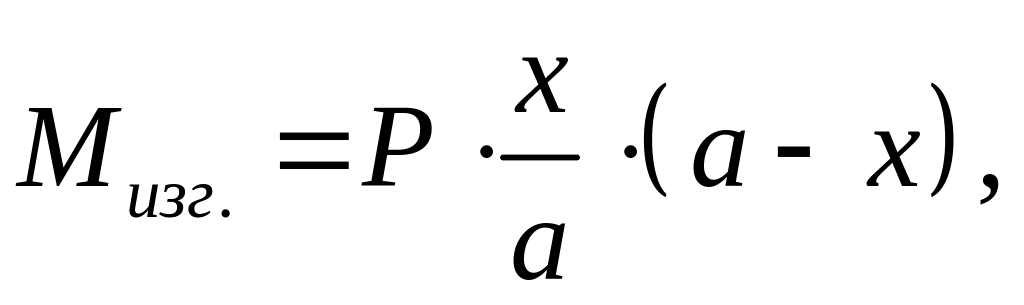(2.80)

где Р – максимальное усилие прокатки;

х – расстояние от середины шейки валка до места приложения усилия, х= мм;

а – расстояние между центрами двух шеек валка а= 3072,5 мм.

После этого напряжение изгиба бочки валка , МПа рассчитывается по формуле [4]

(2.81)

где D_к – катающий диаметр бочки валка, мм.

Строем эпюру изгибающих моментов валка:

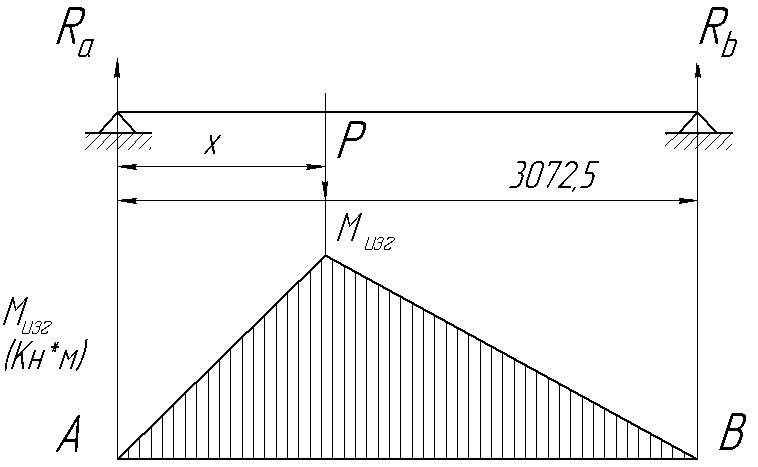
Рисунок 1 – Эпюра изгибающих моментов валка