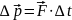Угловой путь и угловое ускорение.
Угловое ускорение – это физическая величина равная отношению изменения угловой скорости к интервалу времени, за который оно произошло.
– угловое
ускорение 
в
этом движении – величина постоянная,
так как 
=
const:
ср = мгн = const.
; 
.
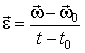
(45)
Единица измерения углового ускорения:
[e]
= 
.
Если
вращение около закрепленной оси (рис.
36), то направления векторов углового
ускорения и угловой скорости совпадают 
при
равноускоренном вращении (w
> w0)
и противоположны 
при
равнозамедленном вращении (w
< w0).
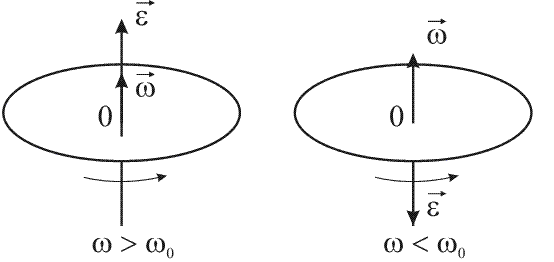
Рис. 36
Таким
образом, направления векторов
и 
аналогичны
направлениям векторов 
и 
.
Соотношения между
и
(46)
аналогичны соотношениям между
и
(21;
22; 23).
Формула мгновенной угловой скорости, как следует из формулы (45), равна:
.
– формула модуля угловой скорости:
.
(46)
– формула углового пути при равнопеременном движении точки по окружности (см. формулу (44) равен:
.
(47)
Подставив
в эту формулу значения средней скорости
и мгновенной скорости 
,
получим другую формулу углового пути
для этого движения:
.
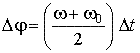
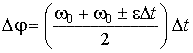
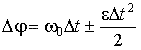(48)
Еще
одну формулу углового пути можно
получить, подставив в формулу (47)
значения
и
интервала времени 
(из
формулы (46)):
.
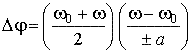
(49)
Итак, угловой путь, угловая скорость и угловое ускорение (47, 48, 49) связаны между собой так же, как и соответствующие им линейные величины S, v и a (24, 26, 29).
– Уравнение равнопеременного движения материальной точки по окружности. Из формулы (48) следует, что
.
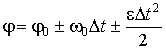(50)
Угловая скорость. Связь с моментом силы.
Углова́я ско́рость — векторная физическая величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:
,
а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону.
Единица измерения угловой скорости, принятая в системах СИ и СГС) — радианы в секунду. (Примечание: радиан, как и любые единицы измерения угла, — физически безразмерен, поэтому физическая размерность угловой скорости — просто [1/секунда]).
Момент силы — векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
Момент силы — производная по времени от момента импульса,
,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
,
То есть если I постоянная, то
,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Второй закон Ньютона и его выражение через импульс.
Второй закон Ньютона: ускорение, приобретаемое материальной точкой, пропорционально вызываемой его силе, совпадает с ней по направлению и обратно пропорционально его массе материальной точки:
Импульс тела – векторная величина, численно равна произведению массы тела на его скорость и имеющая направление скорости тела:
,
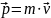где
m
– масса тела,
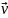- скорость тела.
Второй
закон Ньютона в импульсной форме (при
):
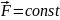