
- •Материальная точка и её поступательное движение.
- •Закон инерции (I закон Ньютона).
- •Инерциальные системы отсчёта.
- •Скорость и ускорение.
- •Кратные и дольные приставки.
- •Вращательное движение материальной точки. Основные параметры.
- •Угловой путь и угловое ускорение.
- •Угловая скорость. Связь с моментом силы.
- •Второй закон Ньютона и его выражение через импульс.
- •Сила и её свойства. Единица силы.
- •Масса и её свойства. Единица массы. Эталон.
- •Закон изменения импульса.
- •Центр масс и закон его движения.
- •II закон Ньютона для вращательного движения.
- •Момент силы и его направление.
Кратные и дольные приставки.
Дольные
Кратные
Название
Обозначение
Множитель
Название
Обозначение
Множитель
деци-
д
10-1
дека-
да
101
санти-
с
10-2
гекто-
г
102
мили-
м
10-3
кило-
к
103
микро-
мк
10-6
мега-
М
106
нано-
н
10-9
гига-
Г
109
пико-
п
10-12
терра-
Т
1012
фенто-
ф
10-15
пета-
П
1015
атто-
а
10-18
экс-
Э
1018
Вращательное движение материальной точки. Основные параметры.
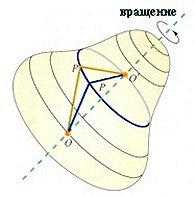
Равномерное движение по окружности
 В
случае равномерного вращения тела
формой траектории его материальных
точек являются окружности радиусов Ri,
где i - порядковый номер выбранной
точки тела. При этом модули их скоростей
остаются постоянными Vi =
const.
В
случае равномерного вращения тела
формой траектории его материальных
точек являются окружности радиусов Ri,
где i - порядковый номер выбранной
точки тела. При этом модули их скоростей
остаются постоянными Vi =
const.
Положение
материальной точки в пространстве
определяется углом ее поворота f относительно
начального значения и радиусом
вектором Ri. За один оборот
радиус-вектор поворачивается на угол
2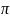 ,
а его конец проходит путь равный 2
·Ri.
,
а его конец проходит путь равный 2
·Ri.
 Для
описания характера вращения используются
следующие характеристики: V -
линейная скорость и
Для
описания характера вращения используются
следующие характеристики: V -
линейная скорость и 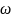 -
угловая скорость. Определение угловой
скорости вводится по аналогии с линейной.
-
угловая скорость. Определение угловой
скорости вводится по аналогии с линейной.
Мгновенная угловая скорость равна скорости изменения угла во времени = df/dt.
Единицей измерения величины является радиан в секунду (рад/c). Направление вектора угловой скорости задается по правилу правого винта (см. рис. 2).
При равномерном вращении
V = 2 R/T, w = f/Dt = 2 /T, где T - время одного полного оборота по окружности (период вращения).
Линейная скорость направлена по касательной в каждой точке траектории.
Угловая и линейная скорости связаны соотношением V = ·R. Для описания вращательного движения вводится понятие частоты вращения n, которая равна числу оборотов тела в единицу времени
n = N/Dt, где N - число оборотов материальной точки за время Dt.
Период обращения связан с частотой вращения соотношением T = 1/n.
Движение по криволинейной траектории Частным случаем такого движения является движение тела по окружности неизменного радиуса с постоянным ускорением. Ускорение вращательного движения тела (угловое ускорение) равно
e = d /dt
Если ускорение с течением времени не изменяется, то
e = D /Dt, где D = - 0 - разность угловых скоростей в произвольный момент времени t и в момент времени t = 0.
Угловое ускорение также как и скорость является векторной величиной. Оно направлено вдоль оси вращения (параллельно вектору угловой скорости, в случае ее возрастания со временем и антипараллельно - в случае ее убывания).
Поскольку ускорение является векторной величиной, то его можно разложить на составляющие. При описании вращательного движения принято использовать понятия касательного и нормального направлений. Соответственно вводятся понятия тангенциального (касательного) и центростремительного (нормального) ускорений.
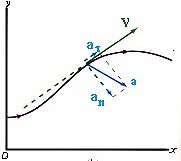 Тангенциальное
ускорение at характеризует
изменение вектора линейной скорости
по величине at =
dV/dt и
направлено по касательной в данной
точке траектории.
Нормальное
ускорение an характеризует
изменение вектора линейной скорости
по направлению an =
V2/R
= w2·R и
сориентировано вдоль нормали (см. рис.
3, на котором показана траектория движения
тела, причем движение происходит с
нарастающей скоростью).
Тангенциальное
ускорение at характеризует
изменение вектора линейной скорости
по величине at =
dV/dt и
направлено по касательной в данной
точке траектории.
Нормальное
ускорение an характеризует
изменение вектора линейной скорости
по направлению an =
V2/R
= w2·R и
сориентировано вдоль нормали (см. рис.
3, на котором показана траектория движения
тела, причем движение происходит с
нарастающей скоростью).
a = an·n + at·t, где n и t - единичные векторы вдоль нормального и тангенциального направлений.
Модуль вектора ускорения равен a = (an2 + at2)1/2. Тангенциальное и угловое ускорения связаны между собой соотношением at = e·R.
