22.1. О движении инерциоидов
Под инерциоидами сегодня понимают транспортные устройства, якобы перемещающиеся под действием только внутренних сил. Покажем, что это не так.
Рассмотрим простую задачу. Ниже представлена простая математическая модель одного из инерциоидов – “движителя Савелькаева” и дано в рамках классической механики объяснение достигаемого эффекта, не требующее привлечения нового для науки понятия. Расчётная схема представлена на Рис 22.2.
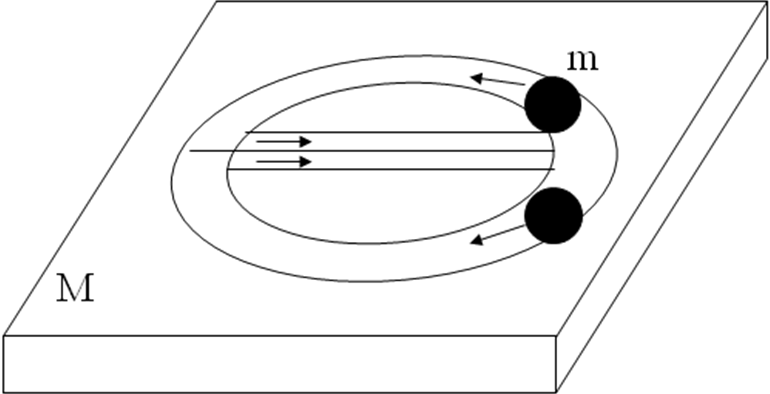
Рис.22.2
Основными
частями движителя Савелькаева, как
механической системы, являются платформа
массы
,
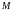движущаяся по какой-то поверхности, и
два массивных
шара
с массами
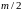каждый, приводимые в движение внутренним
двигателем. Эти шары за один цикл
перемещения платформы совершают два
типа движения: на прямом ходе в первый
промежуток времени
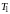центры масс шаров движутся в течение
половины оборота по кругу радиуса
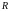допустим
для простоты с
постоянной угловой скоростью
.
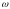На обратном ходе в течение времени
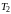шары совершают возвратное равномерное
прямолинейное
движение.
Составим
уравнение движения модели движителя
по оси
с учетом относительного движения шаров,
принимаемых за материальные точки. В
этом случае система как целое имеет
одну
степень свободы по оси
,
так как движение материальных точек
является заданным. Будем
считать, что имеет место вязкое
сопротивление движению.
Запишем уравнение Лагранжа.
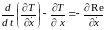
Здесь:
,
,
-
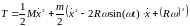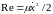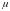- коэффициент
вязкого
трения.
Таким образом, при учете силы вязкого трения, действующей на платформу, уравнение движения системы для прямого хода в ПВТ примет вид:
.
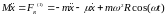Это уравнение решается аналитически. Запишем решение этого уравнения:
,
,
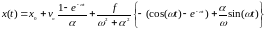где
,
,
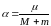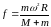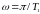
Уравнение движения для обратного хода в ПВТ примет вид:
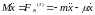
Решение этого уравнения выглядит так:
,
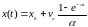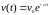
Тогда
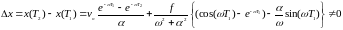
Приведенные решения показывают, что математическая модель адекватно описывает закон движения “гравитационного” движителя Савелькаева.
Важно
отметить, что на прямом и обратном
движениях на платформу действуют разные
силы
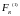и
.
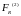А это значит, что и разные
импульсы этих сил
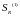и
.
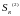Это существенно в связи с тем, что Вам
известна теорема Суднишникова о
влиянии формы импульса силы
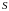на перемещение
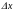массы
.
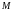В
нашем случае:
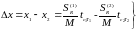
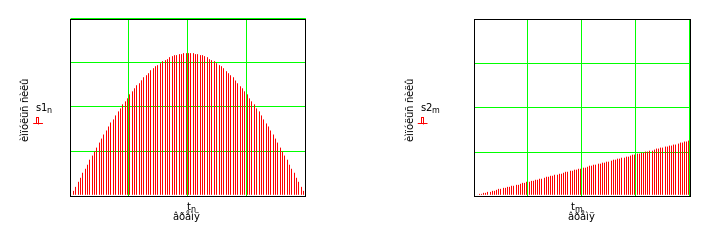
На
Рис.22.3 изображены импульсы сил
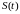шаров в движителе для прямого и обратного
хода.
прямой ход Рис.22.3 обратный ход
Анализ
Рис.16.3 показывает, что
для прямого
и обратного хода и импульсы сил и
различны.
Это означает, что перемещение платформы
как целого происходит и полностью
объясняется как вышеприведенными
решениями, так и теоремой Суднишникова.
При этом отпадает необходимость введения
нового понятия “динамическое
гравитационное поле”
по Савелькаеву.
Лекция №23
МАЛЫЕ КОЛЕБАНИЯ МЕХАНИЧЕСКИХ СИСТЕМ ОКОЛО ПОЛОЖЕНИЯ УСТОЙЧИВОГО РАВНОВЕСИЯ
23.1 Введение
Теория колебаний, начав свое развитие с исследования движения математического маятника, превратилась в самостоятельную дисциплину с весьма сложным математическим аппаратом. На протяжении20-века и сегодня она быстро развивается, что объясняется её значением для современной техники: авиа – ракетостроения, машиностроения, приборостроения, автомобилестроения, медицины и т. д. Создание новейших вибротехнологий, систем виброзащиты, вибродиагностики и многого другого – актуальнейшая задача современной прикладной механики.
В этой лекции остановимся только на ряде принципиально важных и простейших моментов теории колебаний механической системы с одной степенью свободы около положения устойчивого равновесия, необходимых для дальнейшего изучения теории колебаний в спецкурсах. Учтём, что основы физики колебаний Вы уже изучили в курсе физики. Причём, приличный по объёму в часах и количеству лабораторных работ раздел курса физики. Для краткого напоминания этот материал приведён на плакатах в Приложении П.3.2.