
- •21.2 Вычисление обобщенных сил инерции по Лагранжу, Аппелю и Нильсену
- •21.3 Уравнения Лагранжа, Аппеля, Нильсена
- •21.4 Алгоритм составления уравнений лагранжа (нильсена) и решения задач динамики
- •Лекция №22
- •22.1. Формы записи уравнения движения и их решение.
- •22.1. О движении инерциоидов
- •Лекция №23
- •23.1 Введение
- •23.2 Определение положения равновесия
- •23.3 Устойчивость положения равновесия
- •Лекция №24
- •23.1 Пример на малые колебания механической системы с одной степенью свободы около положения
- •Необходимо, прежде всего, найти уравнение и закон движения груза 1.
- •23.2 О вибромеханике в нгту
- •Лекция № 25
- •25.1 Введение
- •25.2 Постулат максвелла
- •25.3. Первая электромеханическая аналогия
- •25.4. Использование уравнений лагранжа для расчёта чисто электрических систем
- •25.5. Пример использования уравнений лагранжа –
- •Лекция № 26
- •26.1 О динамике уПравЛяЕмых систем. Введение
- •26.1. МеханиКа программных жвижений
- •26.2 Системы с дифференциальными связями
- •27.1. Итоги курса
- •27.2. Неразрушающий удар твёрдых тел как процесс
- •27.3. О достижениях нгту в области изучения ударных процессов и создания ударной испытательной техники
Лекция №22
22.1. Формы записи уравнения движения и их решение.
В обычной общепринятой классической форме (ПОКФ).
В Представлении Взаимодействия Движений (ПВД).
В Представление Взаимодействия Тел (ПВТ).
В Представление “форма Коши” (ПФК).
Когда и для чего применяются эти формы записи уравнений движения?
Разберём этот очень важный для практики вопрос на примере решения конкретной задачи. Рассмотрим систему с двумя степенями свободы, представленную на Рис. 22.1.

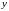
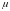

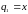
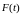


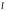
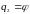
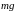
Рис. 22.1
Уравнения движения такой системы запишем по Нильсену:
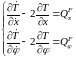 .
.
По завершению всех вычислений и преобразований получим уравнения движения системы в обычной классической форме: в обобщённых ускорениях, скоростях, координатах:
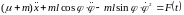
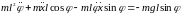
В такой форме записи все компоненты “собраны в кучу”, далеко не для всех сразу просматривается их физический смысл, не прозрачен алгоритм их дальнейшего решения.
б) Представление Взаимодействия Движений
Это Представление даёт возможность понять, как происходит в системе взаимодействие её движений, их “перекачка” друг в друга. Например, в случае сферического движения твёрдого тела это даёт понимание Механики процесса движения.
Это Представление получаем из ПОКФ так. В левой части уравнений оставляем компоненты, описывающие чистые - парциальные движения, а в правую сторону переносим всё остальное. На примере этой задачи видим, что не только задаваемые силы и моменты возбуждают движения системы, но и компоненты сил инерции делают это и обеспечивают взаимодействие разных движений системы. Причём, эти компоненты сил инерции являются Сторонними по отношению к парциальному движению и выступают в качестве реакций внутренних Инерционных Связей. В нашей задаче система уравнений в ПВД выглядит так:
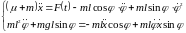 .
.
В
данной механической системе происходит
два динамически
связанных движения по
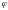 и по
и по
 .
Здесь в роли реакций внутренних
инерционных связей
выступают эйлеровы
силы и моменты сил инерции.
.
Здесь в роли реакций внутренних
инерционных связей
выступают эйлеровы
силы и моменты сил инерции.
в) Представление Взаимодействия Тел
Это Представление подобно 2-му закону Ньютона для каждого тела с учётом всех задаваемых и сторонних сил, действующих на тело. Это даёт возможность понимать и исследовать причины движения каждого тела. Оно получается из предыдущего так. В левой части остаются силы инерции или их моменты “собственного движения” – парциальные силы (моменты) инерции. В правую часть переносится всё остальное, включая и сторонние для данного движения силы инерции. Таким образом, становится понятным, какие силы и моменты приводят в движение это тело.
В нашей задаче уравнения движения системы в ПВТ будут выглядеть так:
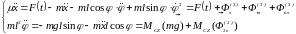 .
.
г) Представление “форма Коши”
Заметим, что с точки зрения математики динамика механической системы, рассматриваемой в нашей задаче, описывается системой двух связанных неоднородных, нелинейных дифференциальных уравнений второго порядка. Аналитическое решение её затруднительно. Возникает вопрос о её численном решении на ПК. Как известно, это делается с использованием ПФК.
Оставляя в левой части “чистые” высшие производные, приведём систему уравнениё к первому порядку. В результате с начала получим:
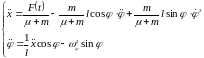 .
И далее
.
И далее
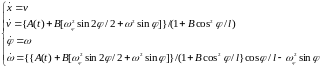
Здесь:
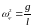 ,
,
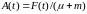 ,
,
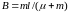 .
.
Это и есть Представление уравнений движения в форме Коши. Далее решаем эту систему уравнений на ПК.
Следует заметить, что научная и учебная практики показывают, что не всякую систему уравнений можно привести к форме Коши. Тогда приходится искать другие способы решения задачи.
Введение этих Представлений позволяет многое понять при решении не только учебных, но, прежде всего реальных научных и технических задач. Например, применение ПВТ совместно с теоремой Суднишникова позволяет дать простое классическое объяснение движения инерциоидов. В науке до сих пор нет единой точки зрения на объяснение их перемещений. У нас с вами есть - классическое!
