
- •21.2 Вычисление обобщенных сил инерции по Лагранжу, Аппелю и Нильсену
- •21.3 Уравнения Лагранжа, Аппеля, Нильсена
- •21.4 Алгоритм составления уравнений лагранжа (нильсена) и решения задач динамики
- •Лекция №22
- •22.1. Формы записи уравнения движения и их решение.
- •22.1. О движении инерциоидов
- •Лекция №23
- •23.1 Введение
- •23.2 Определение положения равновесия
- •23.3 Устойчивость положения равновесия
- •Лекция №24
- •23.1 Пример на малые колебания механической системы с одной степенью свободы около положения
- •Необходимо, прежде всего, найти уравнение и закон движения груза 1.
- •23.2 О вибромеханике в нгту
- •Лекция № 25
- •25.1 Введение
- •25.2 Постулат максвелла
- •25.3. Первая электромеханическая аналогия
- •25.4. Использование уравнений лагранжа для расчёта чисто электрических систем
- •25.5. Пример использования уравнений лагранжа –
- •Лекция № 26
- •26.1 О динамике уПравЛяЕмых систем. Введение
- •26.1. МеханиКа программных жвижений
- •26.2 Системы с дифференциальными связями
- •27.1. Итоги курса
- •27.2. Неразрушающий удар твёрдых тел как процесс
- •27.3. О достижениях нгту в области изучения ударных процессов и создания ударной испытательной техники
Возможные
перемещения
 ,
называют со времён Л.Эйлера – изохронными
вариациями
(одномоментные,
в данный момент времени вариации
координат). Они кинематически
и линейно независимымы.
Тогда исходную систему общих уравнений
динамики можно будет переписать так:
,
называют со времён Л.Эйлера – изохронными
вариациями
(одномоментные,
в данный момент времени вариации
координат). Они кинематически
и линейно независимымы.
Тогда исходную систему общих уравнений
динамики можно будет переписать так:

В
результате получим систему
уравнений движения в обобщенных силах:
 ,
как наиболее
общую
из ковариантных форм.
,
как наиболее
общую
из ковариантных форм.
21.2 Вычисление обобщенных сил инерции по Лагранжу, Аппелю и Нильсену
“По Лагранжу”. Наиболее привычная на сегодня и употребляемая в инженерной практике для описания динамики голономных систем и неголономных систем с линейными по скоростям уравнениями связей, – форма вычисления обобщенных сил инерции – “по Лагранжу”. Она исторически связана с уравнениями Лагранжа второго рода (конец 18-го века), которые рассмотрим далее. Тогда

Здесь
 .
.
“По
Аппелю”. Ковариантные
уравнения Аппеля
(начало 20 века) хотя и имеют наипростейший
вид, однако
на практике
составляются
гораздо более громоздко и применяются
в основном при решении задач динамики
неголономных и управляемых систем с
уравнениями связей – программами
движений, до линейных по ускорениям.
Здесь
 вычисляются так:
вычисляются так:
 и
и
 ,
,
 - энергия
ускорений
(функция
Аппеля).
- энергия
ускорений
(функция
Аппеля).
“По Нильсену”. Уравнения Нильсена (середина 20-го века) – эта форма уравнений применятся в основном для решения чисто механических задач голономных и неголономных систем вплоть до нелинейных по скоростям связей. Здесь определяются так:
 .
.
21.3 Уравнения Лагранжа, Аппеля, Нильсена
Эти три хорошо известные ковариантные формы уравнений движения получаются подстановкой в уравнения движения в обобщённых силах

соответствующих выражений для обобщённых сил инерции . Тогда
 -
система
уравнений Лагранжа 2-го рода.
-
система
уравнений Лагранжа 2-го рода.
Здесь уместно отметить, что для потенциальных систем (и обощеннопотенциальных систем) удобно ввести функцию Лагранжа – Кинетический потенциал (аналог Свободной энергии в термодинамике), как одну из энергетических мер, так:
 (Дж)
(Дж)
Тогда, для таких систем, уравнения Лагранжа примут вид:
 .
.
В
общем случае, при наличии
 разной природы: потенциальных,
диссипативных, зависящих от времени…,
уравнения Лагранжа примут вид:
разной природы: потенциальных,
диссипативных, зависящих от времени…,
уравнения Лагранжа примут вид:

Аналогично получим и системы уравнений Аппеля и Нильсена:
 -
система
уравнений Аппеля.
-
система
уравнений Аппеля.
 -
система
уравнений Нильсена.
-
система
уравнений Нильсена.
Сегодня известен ещё ряд ковариантных форм уравнений движения, однако в нашем курсе мы их не рассматриваем.
21.4
Вычисление кинетической энергии как
 .
.
Выразим кинетическую энергию через обобщенные скорости и координаты.
Кинетическая
энергия
 определяется как
определяется как
 .
.
Учтём,
что
 и
и
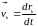 .
Тогда
.
Тогда
 и
и
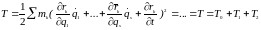 .
.
Здесь
 ,
,
 ,
,

Введем обозначения
 ,
,

Тогда
 ,
,
 и
и

Коэффициенты
 принято называть обобщенными
коэффициентами инерции.
Здесь
принято называть обобщенными
коэффициентами инерции.
Здесь .
Коэффициенты
.
Коэффициенты
 - гиростатические
коэффициенты.
Заметим, что
и
не зависят
от обобщенных скоростей
- гиростатические
коэффициенты.
Заметим, что
и
не зависят
от обобщенных скоростей
 .
.
При
стационарных связях время t
явно не входит
в
 .
Все частные производные
.
Все частные производные
 будут равны нулю, а значит и
будут равны нулю, а значит и
 ,
и
,
и
 .
Поэтому, в этом случае, кинетическая
энергия есть квадратичная
форма
обобщенных скоростей и всегда определенно
положительна.
.
Поэтому, в этом случае, кинетическая
энергия есть квадратичная
форма
обобщенных скоростей и всегда определенно
положительна.

21.4 Алгоритм составления уравнений лагранжа (нильсена) и решения задач динамики
Эти уравнения активно применяются в наше время в механике, электромеханике и мехатронике в силу удобной простоты их составления по алгоритму.
Алгоритм:
Выделяем механическую систему и определяем число её степеней свободы.
Выбираем удобные для решения данной задачи обобщенные координаты, в количестве S, где S – число степеней свободы.
Записываем систему уравнений движения в одной из форм, например в форме Лагранжа (Нильсена).
Записываем кинетическую энергию как сумму кинетических энергий частей и используем, в том числе теорему Кёнига.
Проводим кинематический анализ движения тел системы, то есть выражаем
 через
искомые величины.
через
искомые величины.Компонуем выражение для кинетической энергии системы в виде:
 .
.Вычисляем левые части уравнения.
Проводим силовой анализ задаваемых сил и пар сил, действующих на систему, и изображаем на расчетной схеме.
Вычисляем обобщенные задаваемые силы, каким-нибудь из известных способов.
Компонуем уравнения движения (к левой части приравниваем правую). Анализируем их и классифицируем задачу динамики. В конечном счете получаем уравнения движения в обобщенных координатах, скоростях и ускорениях.
Решаем задачу методами математики.
Проводим содержательный анализ полученного решения, делаем проверку и интерпретируем полученный результат.
