
- •Питання державної атестації с математики для студентів першого курсу всіх спеціальностей.
- •Властивості:
- •Призма. Паралелепіпед. Їх елементи та властивості.
- •Властивості призми:
- •Основні елементи:
- •Властивості:
- •Завдання на розв’язування логарифмічної нерівності.
- •Задача на знаходження об’єму циліндра.
- •Область значень – проміжок [-1;1].
- •Площа поверхні призми
- •Завдання для знаходження первісної функції.
- •Задача на знаходження площі поверхні конуса.
- •Былет № 4.
Основні елементи:
Дві грані паралелепіпеда, які не мають загального ребра, називаються протилежними, а які мають загальне ребро - суміжними.
Дві вершини паралелепіпеда, що не належать одній межі, називаються протилежними.
Відрізок, що сполучає протилежні вершини, називається діагоналлю паралелепіпеда.
Довжини трьох ребер прямокутного паралелепіпеда, що мають загальну вершину, називають його вимірами.
Властивості:
Паралелепіпед симетричний щодо середини його діагоналі.
Будь-який відрізок з кінцями, що належать поверхні паралелепіпеда і що проходить через середину його діагоналі, ділиться нею навпіл; зокрема, всі діагоналі паралелепіпеда перетинаються в одній точці і діляться нею навпіл.
Паралельні межі паралелепіпеда паралельні і рівні.
Квадрат довжини діагоналі прямокутного паралелепіпеда дорівнює сумі квадратів трьох його вимірювань.
Завдання на розв’язування логарифмічної нерівності.

Якщо a>1, то логарифмічна функція зростає, тому більшому логарифму відповідає і більше значення виразу, що стоїть під знаком логарифма.
Якщо a<1, то більшому логарифму відповідає менше значення виразу, що стоїть під знаком логарифма.
Задача на знаходження об’єму циліндра.
Візьмемо пласку фігуру, утворену такими прямими: y = R, x = 0, x = h, y = 0 та будемо обертати її навколо осі Ox. Таким чином ми отримуємо тіло обертання, утворене обертанням прямокутника навколо однієї з його сторін, тобто циліндр.
 кінцева формула:
кінцева формула:
![]() Де d — діаметр основи; R —
радіус основи.
Де d — діаметр основи; R —
радіус основи.
Білет № 2
Функція y=cosx, її графік і властивості.

Властивості функції y=cosх:
Обл. визначення - проміжок (-∞;+∞).
Область значень – проміжок [-1;1].
Функція парна, періодична з періодом Т=2П.
Функція зростає при -П+2Пn<х<2Пn, nє Z.
Функція спадає при 2Пn<х<П+2Пn, nє Z.
Функція має максимум у точках (2Пn;0), мінімум у точках (П+2Пn;0), nєZ.
Площа поверхні призми
Площа
поверхні призми дорівнює
![]() ,
де B — площа основи, h — висота, P —
периметр основи.
,
де B — площа основи, h — висота, P —
периметр основи.
Завдання для знаходження первісної функції.
Приклад
Нехай
потрібно взяти інтеграл
![]()
Вводимо нову змінну t = e^x. Тоді dt = e^(x)dx. Інтеграл переписується
![]()
Задача на знаходження площі поверхні конуса.
Приклади:
Висота конуса дорівнює 6см, радіус основи – 8см. Знайдіть бічну поверхню конуса. (Відповідь. см2)
Твірна конуса дорівнює 5см, висота – 4см. Знайдіть площу його повної поверхні. (Відповідь. см2)
Відповідь:
Через дві твірні конуса, кут між якими дорівнює
 ,
проведено переріз, який утворює з
площиною основи конуса кут
,
проведено переріз, який утворює з
площиною основи конуса кут
 .
Знайдіть площу бічної поверхні конуса,
якщо його висота дорівнює
.
Знайдіть площу бічної поверхні конуса,
якщо його висота дорівнює
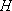 .
(Відповідь.
.
(Відповідь.
 )
)Переріз конуса, який проходить через його вершину, перетинає основу конуса по хорді, яку видно з центра основи під кутом . Знайдіть площу бічної поверхні конуса. (Відповідь.
 )
)
Білет № 3.
Функція y=tgx, її графік і властивості.

Властивості функції y=tgх:
Обл. визначення – всі дійсні числа, крім точок (П/2+2Пn), nєZ.
Область значень – проміжок (-∞;+∞).
Функція непарна, періо-дична з періодом Т= П.
Нулі функції – точки (Пn;0), nєZ.
Функція зростає на всій області визначення.
Функція не має екстремумів.
Об’єм зрізаної піраміди.
![]()
Завдання на розв’язування показникового рівняння.
Найпростіше показникове рівняння a^(x) = b де a і b не залежать від x.
A^(x) = b; За визначенням логарифму x = log(a) b
5^(x) = 11
за визначенням логарифму x = log(5) 11
Задача на знаходження кута між векторами в просторі.
