31. Гармоническими колебаниями называются такие колебания, при которых колеблющаяся величина меняется от времени по закону синуса или косинуса.

Уравнение гармонических колебаний имеет вид:

,

где A - амплитуда колебаний (величина наибольшего отклонения системы от положения равновесия); - круговая (циклическая) частота. Периодически изменяющийся аргумент косинуса - называется фазой колебаний. Фаза колебаний определяет смещение колеблющейся величины от положения равновесия в данный момент времени t. Постоянная φ представляет собой значение фазы в момент времени t = 0 и называется начальной фазой колебания. Значение начальной фазы определяется выбором начала отсчета. Величина x может принимать значения, лежащие в пределах от -A до +A.

Промежуток времени T, через который повторяются определенные состояния колебательной системы, называется периодом колебаний. Косинус - периодическая функция с периодом 2π, поэтому за промежуток времени T, через который фаза колебаний получит приращение равное 2π, состояние системы, совершающей гармонические колебания, будет повторяться. Этот промежуток времени T называется периодом гармонических колебаний.

Период гармонических колебаний равен: T = 2π/ .

Число колебаний в единицу времени называется частотой колебаний ν.

Частота гармонических колебаний равна: ν = 1/T. Единица измерения частоты герц (Гц) - одно колебание в секунду.

Круговая частота = 2π/T = 2πν дает число колебаний за 2π секунд.

33. Гармоническим осциллятором называется система, совершающая колебания, описываемые дифференциальным уравнением

Физический маятник — это твердое тело, которое совершает колебания под действием силы тяжести вокруг неподвижной горизонтальной оси, которая проходит через точку О, не совпадающую с центром масс С тела. Если маятник из положения равновесия отклонили на некоторый угол α, то, используя уравнение динамики вращательного движения твердого тела, момент M возвращающей силы

Из формулы вытекает, что при малых колебаниях физический маятник совершает гармонические колебания с циклической частотой ω₀ и периодом

34. Гармоническим осциллятором называется система, совершающая колебания, описываемые дифференциальным уравнением

Пружинный маятник — это груз массой m, который подвешен на абсолютно упругой пружине и совершает гармонические колебания под действием упругой силы F = –kx, где k — жесткость пружины. Уравнение движения маятника имеет вид

Из формулы вытекает, что пружинный маятник совершает гармонические колебания по закону х = Асоs(ω0t+φ) с циклической частотой

и периодом

Формула верна для упругих колебаний в границах, в которых выполняется закон Гука, т. е. если масса пружины мала по сравнению с массой тела. Потенциальная энергия пружинного маятника, используя (2) и формулу потенциальной энергии предыдущего раздела, равна

35. Дифференциальное уравнение свободных затухающих колебание линейной системы имеет вид: d²x/dt²+2dx/dt+₀²x=0. Здесь x- изменяющаяся при колебаниях физическая характеристика системы, =const>0 – коэффициент затухания, а ₀- циклическая частота свободных незатухающих колебаний той же системы, т.е. в отсутствие потерь энергии(при =0). Решением этого уравнения затухающих колебаний имеет вид: x=A₀e^-tcos(t+£). Здесь =₀²-²), а постоянные величины А₀ и £ зависят от начальных условий, т.е. от значений x и dx/dt в начальный момент времени (t=0).

Коэффициент затухания - количественная характеристика сопротивления колеблющейся системы колебательному движению.

Логарифмический декремент затухания - безразмерная характеристика затухающих колебаний, измеряемая натуральным логарифмом отношения двух последовательных максимальных отклонений колеблющейся величины в одну и ту же сторону.

ля характеристики интенсивности затухания вводят понятие логарифмического декремента затухания. Пусть Т - условный период затухающего колебания, Аn и An+1 - амплитудные значения функции x(t) для двух ее последовательных экстремумов (см. рис. 10.7). Величина d, равная:

d = ln(Аn /An+1) (10.12)

называется логарифмическим декрементом затухания. Выясним связь между d и d:

d = ln( Аn /An+1) = ln(A0·e - d·t/A0·e - d·(T + t)) = ln(e d·T) = d·T = d. (10.13)

Используя уравнение (10.13), можно преобразовать закон изменения амплитуды:

An = A0·e-d·t = A0·e-d·T·t/T = A0·e-d·n, (10.14)

где n = t/T - число колебаний за время t.

An = A0·e-d·n.

Если n = 1/d, то A0/An = e.

Величина 1/d равна числу колебаний, за которое их амплитуда уменьшается в е раз.

Если значение d невелико (d << 1), то можно показать, что

(An - An+1)/An = d. (10.15)

Логарифмический декремент связан с другой важной характеристикой колебаний - добротностью q следующим соотношением:

q = p/d.

36. Вынужденные колебания осциллятора под действием синусоидальной силы. ; ma = F ; m d2 x / dt (ст.2) = F ; Fупр = - kx ; Fтр = - b dx / dt ; F = F0 sinΩt ; (d2 x / dt (ст.2)) + (2 БЕТА dx / dt) + w 0 (ст.2) = (F0 / m) sinΩt ; Это дифференциальное уравнение описывает вынужденные колебания. В общем случае общее решение этого неоднородного дифференциального уравнения имеет вид: X(t) = X1(t) + X2(t) ; X1(t) является общим решением однородного диф. уравнения, описывающего свободный гармонический затухающий осциллятор. Видно, что после начала действия вынуждающей силы возникает сложный колебательный процесс, состоящий из суммы 2х колебаний – затухающего колебания X1(t) с частотой wt и незатухающего колебания с частотой Ωt. X1(t) за достаточно небольшой промежуток времени затухает и остается только одно колебание с частотой вынужденной силы Ω0. Это время, в течении которого X1(t) затухает, называется временем установки вынужденных колебаний.

37.

38.

39. Бегущая волна – это волна, которая переносит энергию.

Стоячая волна энергии не переносит. Стоячие волны образуюся в результате интерференции (наложения) 2х одинаковых, противоположных по направлению волн. Энергия, переносимая волной количественно характеризуется вектором плотности потока энергии, вектором Умова.

y = A sin (wt + φ0).

40. Фа́зовая ско́рость — скорость перемещения точки, обладающей постоянной фазой колебательного движения, в пространстве вдоль заданного направления. Обычно рассматривают направление, совпадающее с направлением волнового вектора, и фазовой скоростью называют фазовую скорость, измеренную именно в этом направлении, если противное не указано явно (то есть если явно не указано направление, отличное от направления волнового вектора).

X = 2ПИ / λ – ВОЛНОВОЕ ЧИСЛО (волновой вектор) – вектор, направление которого совпадает с направлением движения волны.

y (x, t)= Asin (wt – kx + φ0) – уравнение плоской синусоидальной бегущей волны, распространяющейся в положении направления оси X. Учитывая формулу Эйлера, эту плоскую волну можно записать в виде

y (x, t) = A e (ст. i (wt – kx + φ)) ; sinx(t) = A sin (wt – kx + φ0).

Фазовая скорость волны – это скорость распространения точки с постоянной фазой – Ф = const ; v = dx / dt ; Дифференцируем Ф и получаем:

dФ = d (wt – kx – φ0) = wdt – kdx  dx / dt = w/k – фазовая скорость волны!

41. Пpинцип супеpпозиции волн гласит, что волны от pазличных источников не взаимодействуют дpуг с дpугом и что сложное волновое поле от двух или большего числа источников находится путем геометpического сложения волн от отдельных источников, т.е.

Это очень важный пpинцип. Он позволяет не только складывать волны, но и pаскладывать их, напpимеp, на независимые синусоидальные волны. Это означает, что любую волну, т.е. волну пpоизвольного пpофиля, всегда можно пpедставить как сумму синусоидальных волн с pазличными амплитудами, с pазличными фазовыми скоpостями, с pазличными частотами и с pазличными начальными фазами.

Групповая скорость – это скорость перемещения в пространстве этого волнового пакета.

S1 = Asin (wt - kx) ; S2 = Asin [(w + dw) t – (k + dk) x] ; S = S1+S2;

S=2Asin (wt – kx) cos ((xdk – tdw) / 2) ; xdk – tdw = const ; u = dx/dt ;

d (xdk - tdw) = 0; dx dk – dt dw = 0  dx / dt = dw / dk ; u = dw / dk ;

w = kv ; dw = kdv + vdk ; u = v + k (dv / dk) ; k = 2ПИ / λ ;

dk = (2ПИ/ λ(ст.2)) dλ; u = v – λ (dv / dλ) ; Из этого выражения видно, что в зависимости от свойств среды групповая скорость может быть как больше, так и меньше фазовой скорости. Если среда не дисперсирующая, то dv / dλ = 0 и u = Ф. В теории относительности доказывается, что групповая скорость волны не может быть больше скорости света.

42. Эффект Доплера описывает сдвиг частоты сигнала в зависимости от относительного движения источника и приемника. Так волна, посланная источником, который удаляется от приемника, будет приниматься им на меньшей частоте по сравнению с волной от неподвижного источника или от источника, приближающегося к приемнику. Если же приемник приближается к неподвижному источнику, то частота принимаемой им волны будет больше по сравнению с неподвижным приемником или приемником, удаляющимся от источника. Это явление обнаружил Христиан Доплер в 1842 году.

Источник и приемник покоятся от­носительно среды, т.е. v_ист=v_пр=0. Если v — скорость распространения звуковой волны в рассматриваемой среде, то длина волны =vT=v/v₀. Распространяясь в среде, волна достигнет приемника и вы­зовет колебания его звукочувствительного элемента с частотой

=v/=v/(vT)=₀

Следовательно, частота v звука, которую зарегистрирует приемник, равна частоте ₀, с которой звуковая волна излучается источником.

43. Эффект Доплера описывает сдвиг частоты сигнала в зависимости от относительного движения источника и приемника. Так волна, посланная источником, который удаляется от приемника, будет приниматься им на меньшей частоте по сравнению с волной от неподвижного источника или от источника, приближающегося к приемнику. Если же приемник приближается к неподвижному источнику, то частота принимаемой им волны будет больше по сравнению с неподвижным приемником или приемником, удаляющимся от источника. Это явление обнаружил Христиан Доплер в 1842 году.

Источник приближается к приемни­ку, а приемник покоится, т.е. v_ист>0, v_пр=0. Скорость распространения колеба­ний зависит лишь от свойств среды, поэто­му за время, равное периоду колебаний источника, излученная им волна пройдет в направлении к приемнику расстояние vT (равное длине волны Я) независимо от того, движется ли источник или покоится. За это же время источник пройдет в на­правлении волны расстояние v_истT (рис.224), т.е. длина волны в направле­нии движения сократится и станет равной '=-v_истТ=(v-v_ист)Т, тогда

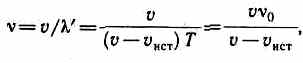
т. е. частота v колебаний, воспринимаемых приемником, увеличится в v/(v-v_ист) раз. В случаях 2 и 3, если v_ист<0 и v_пр<0, знак будет обратным.

44. Эффект Доплера описывает сдвиг частоты сигнала в зависимости от относительного движения источника и приемника. Так волна, посланная источником, который удаляется от приемника, будет приниматься им на меньшей частоте по сравнению с волной от неподвижного источника или от источника, приближающегося к приемнику. Если же приемник приближается к неподвижному источнику, то частота принимаемой им волны будет больше по сравнению с неподвижным приемником или приемником, удаляющимся от источника. Это явление обнаружил Христиан Доплер в 1842 году.

Приемник приближается к источни­ку, а источник покоится, т.е. v_пр>0, v_ист=0. В данном случае скорость распро­странения волны относительно приемника станет равной v+v_пр. Так как длина во­лны при этом не меняется, то

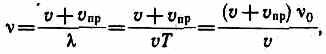
т. е. частота колебании, воспринимаемых приемником, в (v+v_пр)/v раз больше частоты колебаний источника.

45. Эффект Доплера описывает сдвиг частоты сигнала в зависимости от относительного движения источника и приемника. Так волна, посланная источником, который удаляется от приемника, будет приниматься им на меньшей частоте по сравнению с волной от неподвижного источника или от источника, приближающегося к приемнику. Если же приемник приближается к неподвижному источнику, то частота принимаемой им волны будет больше по сравнению с неподвижным приемником или приемником, удаляющимся от источника. Это явление обнаружил Христиан Доплер в 1842 году.

Источник и приемник движутся от­носительно друг друга. Используя резуль­таты, полученные для случаев 2 и 3, можно записать выражение для частоты колеба­ний, воспринимаемых источником:

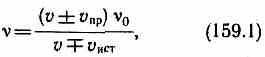
причем верхний знак берется, если при движении источника или приемника про­исходит их сближение, нижний знак — в случае их взаимного удаления. Из приведенных формул следует, что эффект Доплера различен в зависимости от того, движется ли источник или при­емник. Если направления скоростей v_пр и v_ист не совпадают с проходящей через источник и приемник прямой, то вместо этих скоростей в формуле (159.1) надо брать их проекции на направление этой прямой.

46. Макроскопические параметры – параметры значения которых можно определить с помощью приборов, ничего не зная об атомно-молекулярном строении вещества (давление, объем, температура). (Учащиеся записывают определение у себя в тетрадях).

Тепловое движение - беспорядочное движение молекул, атомов и ионов в газах, жидкостях и твердых телах.

Молекулы газов беспорядочно движутся с различными скоростями по всему объему газа.

Молекулы жидкости колеблются около равновесных положений и сравнительно редко перескакивают из одного равновесного положения в другое.

В твердых телах частицы колеблются около положения равновесия.

47. Идеальный газ — математическая модель газа, в которой предполагается, что потенциальной энергией молекул можно пренебречь по сравнению с их кинетической энергией. Между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями.

Модель широко применяется для решения задач термодинамики газов и задач аэрогазодинамики. Например, воздух при атмосферном давлении и комнатной температуре с большой точностью описывается данной моделью. В случае экстремальных температур или давлений требуется применение более точной модели, например модели газа Ван-дер-Ваальса, в котором учитывается притяжение между молекулами.

Изотермический процесс - посмотри в тетради.

48. Идеальный газ — математическая модель газа, в которой предполагается, что потенциальной энергией молекул можно пренебречь по сравнению с их кинетической энергией. Между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями.

Модель широко применяется для решения задач термодинамики газов и задач аэрогазодинамики. Например, воздух при атмосферном давлении и комнатной температуре с большой точностью описывается данной моделью. В случае экстремальных температур или давлений требуется применение более точной модели, например модели газа Ван-дер-Ваальса, в котором учитывается притяжение между молекулами.

Изобарный процесс - посмотри в тетради.

49. Идеальный газ — математическая модель газа, в которой предполагается, что потенциальной энергией молекул можно пренебречь по сравнению с их кинетической энергией. Между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями.

Модель широко применяется для решения задач термодинамики газов и задач аэрогазодинамики. Например, воздух при атмосферном давлении и комнатной температуре с большой точностью описывается данной моделью. В случае экстремальных температур или давлений требуется применение более точной модели, например модели газа Ван-дер-Ваальса, в котором учитывается притяжение между молекулами.

Изохорный процесс - посмотри в тетради.

50. Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Клапейрона — Менделеева) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:

где

P— давление,

V_M— молярный объём,

R— универсальная газовая постоянная

T— абсолютная температура,К

Так как где - количество вещества, а , где m- масса, M- молярная масса, уравнение состояния можно записать: Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона.