
- •Простые ставки процентов, основные понятия и формулы. Точные и обыкновенные проценты. Доходность финансовых операций в условиях инфляции (при использовании простых ставок процентов).
- •Особенности расчетов при операциях с векселями
- •Дисконтирование, его сущность и виды. Расчеты с использованием простых ставок процентов и простых учетных ставок в условиях инфляции.
- •Простые учетные ставки, сложные ставки процентов основные понятия и формулы. Понятие номинальной и эффективной ставки сложных процентов. Точный и смешанный способ расчета сложных процентов.
- •Формулы для учетной ставки
- •Расчеты в условиях инфляции при использовании различных ставок.
- •16. Долгосрочные инвестиционные проекты. Основные параметры, используемые при выборе вариантов инвестиционных проектов. Их сущность, взаимосвязь.
16. Долгосрочные инвестиционные проекты. Основные параметры, используемые при выборе вариантов инвестиционных проектов. Их сущность, взаимосвязь.
Долгосрочные инвестиционные проекты предполагают вложения (инвестиции) разнесенные по времени и поступления (выручку), а также разнесенные во времени. Проекты считаются выгодными или эффективными, если суммарные поступления превышают суммарные затраты. Проблема в том, что все платежи в разных точках временной оси и непосредственно их складывать нельзя. Поэтому их нужно в начале привести в одну точку. Это точка 0 –начало проекта или момент времени, совпадающий с первой инвестицией. Поскольку платежей много ставка сложная. Почти 99% эффективная. Все платежи дисконтируются. Ставка обычно выбирается как некая среднерыночная ставка. Это может быть инфляция или среднерыночные отрасли.
17. Дисконтирование, его сущность и виды. Основные правила и последовательность расчетов с векселями.(Вопрос5).
18. Сравнение вариантов долгосрочных инвестиций по совокупности показателей.
19. Простые учетные ставки, сложные ставки процентов основные понятия и формулы. Понятие номинальной и эффективной ставки сложных процентов. Точный и смешанный способ расчета сложных процентов.(Вопрос8).
20. Расчеты, связанные с изменениями условий контракта. Расчет суммы последнего платежа при нескольких сроках платежей.
Изменение условий ренты по существу означает замену одной ренты другой. Если замена базируется на принципе финансовой эквивалентности, то из этого следует равенство современных величин обеих рент.
В качестве примера приведем случай, когда внесение первого взноса ренты переносится на более поздний срок (t лет, месяцев). При этом общая продолжительность ренты, размеры платежей могут оставаться прежними или измениться.
Пусть первоначально имеется постоянная рента постнумерандо имеет параметры R1 и n1. Необходимо конвертировать ренту, отсрочив выплаты на t лет и заменив параметры на R2 и n2.
В соответствии с принципом финансовой эквивалентности должны быть равны современные величины первоначальной и отсроченной рент.
А1 = А2.
Вычислим их на момент начала первоначальной ренты.
![]()
![]() ,
,
где
![]() ,
,
![]() —
коэффициенты приведения первоначальной
годовой
ренты;
—
коэффициенты приведения первоначальной
годовой
ренты;
![]() — дисконтный
множитель за период t,
на который
отложена рента.
— дисконтный
множитель за период t,
на который
отложена рента.
Рассмотрим один из примеров замены параметров ренты.
Пример 10. Банк предлагает к продаже объект залогового имущества стоимостью 400 тыс. руб. Банк выставил условия продажи: стоимость объекта погашается ежегодными равными платежами, вносимыми в конце года, срок погашения 4 года, сложная процентная ставка 4% годовых, проценты начисляются два раза в год. Покупатель предлагает свои условия: платежи производить 2 раза в год и проценты на них начислять два раза в год, по ставке 6% годовых, со сроком выплаты 6 лет. Определить величину рентного платежа, предложенного продавцом и покупателем.
Имеем: А1 = А2 = 400 тыс. руб. n1 = 4 n2 = 6 J1 = 0,04 j2 = 0,06 m1 = m2 = 2 p1 = 1 p2 = 2 |
Решение: По условию имеются две эквивалентные ренты с известной общей современной стоимостью. Известны все параметры рассматриваемых рент, за исключением размеров платежей. Найдем их с помощью формул таблицы 1. |
R1 - ? R2 - ? |
|
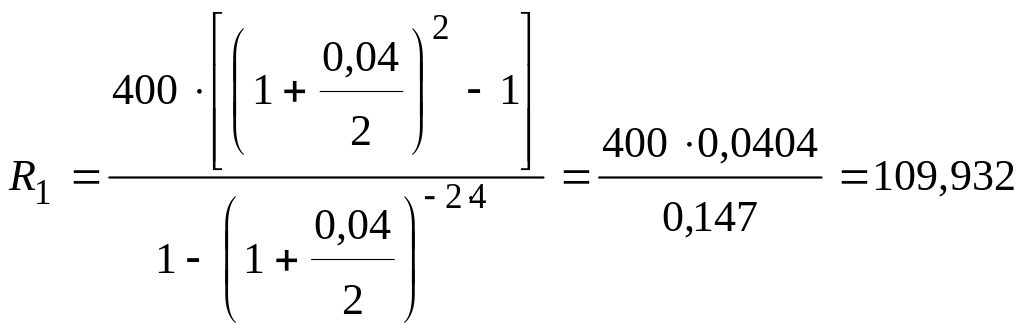 тыс.
руб.
тыс.
руб.
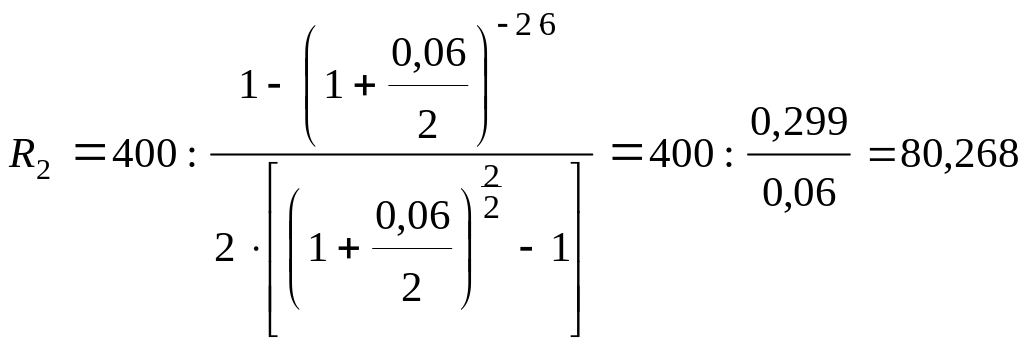 тыс.
руб.
тыс.
руб.
21. Финансовая эквивалентность обязательств. Эквивалентность различных ставок. Вывод формул эквивалентности.(Вопросы 9, 10)
22. Расчет средней доходности однотипных финансовых инструментов. Доходность с учетом налогообложения.(Вопрос 5)
Средняя доходность
1 способ: Через формулу средне - арифметической взвешенной
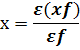
![]() i-вариант
х (то, что нужно найти). f-
то на что умножаем (частота Pn
); I-
W-
объемный признак.
i-вариант
х (то, что нужно найти). f-
то на что умножаем (частота Pn
); I-
W-
объемный признак.
![]()
2
способ:![]() )
)
![]()
![]()
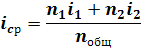
23. Расчеты по сложным и учетным ставкам. Учет инфляции.(Вопрос 8)
Инфляция – это сложное, многофакторное явление. Внешнее проявление инфляции-это рост цен. Рост цен рассчитывается службой государственной статистики Росстат.
Инфляция харак-ся 2 стандартными показателями:
1. Индекс инфляции: Iи- он показывает во сколько раз выросли цены.
2.
Уровень или темп инфляции: ![]() - показывает на сколько процентов выросли
цены.
- показывает на сколько процентов выросли
цены.
![]()
Соответственно индекс- темп роста, а уровень- темп прироста.
На 1 этапе стандартный показатель характеризующий инфляцию перечитывают в показатель за срок конкре тный, при этом используют взаимосвязь между цепными и базисными индексами. Произведение нескольких цепных индексов – базисный индекс.
Непосредственные расчеты в условиях инфляции:
1 тип: есть какой-то показатель, который нужно очистить от инфляции.
2 тип: мы имеем какой-то показатель о реальном выражении и пытаемся узнать, какая инфляция нам достичь этих показателей.
1) В условиях инфляции все показатели бывают неочищенные от инфляции или номинально брутто-показатели.
2)Очищенные от инфляции реальные или нетто-показатели, т.е. в реальном выражении.
24. Принцип временной стоимости денег. Ставки, их виды и условия их применения.(Вопрос )
Деньги обладают свойством увеличивать свою стоимость в течении определенного времени, но они растут не существенно. При не высокой процентной ставке можно считать, что деньги сегодняшние и деньги будущие приблизительно равны. Следовательно деньги, которые находятся в равных точках временной оси непосредственно сравнивать нельзя. Сначала их нужно привести в одну точку и там сравнивать.
Формула для нахождения процентных денег
I- Процентные деньги; Р- инвестиции, сумма вложений; n- срок операций.
Формула наращения по простой процентной ставке
Увеличение суммы долга за счет присоединения начисленных процентов называют наращением первоначальной суммы долга.
– коэффициент наращения.
Отношение наз-ся коэффициентом наращения. Он показывает во сколько раз выросла вложенная сумма.
По FV находим Р-это наз-ся дисконтированием.
Формула дисконтирования по простым процентным ставкам
Коэффициент дисконтирования
25. Вывод формул обобщающих параметров потоков платежей. В качестве примера разобрать вывод современной стоимости ренты для случая когда: платежи выплачиваются раз в год, проценты начисляются несколько раз в году.(Вопрос 3)
Рентные платежи вносятся один раз в году, а проценты на них начисляются m раз в году. В этом случае начисление процентов каждый раз будет производиться по ставке j/m, где j — номинальная (годовая) ставка сложных процентов.
Величина наращенной суммы ренты постнумерандо будет определяться по формуле:
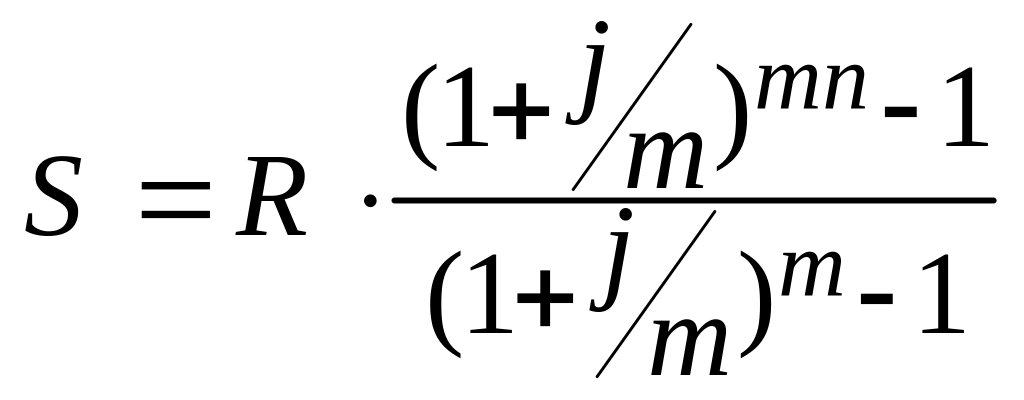 .
(3.4)
.
(3.4)
Величина наращенной суммы ренты пренумерандо в этом случае будет определяться по формуле:
![]() .
(3.5)
.
(3.5)
Пример 2. Несколько изменим условия примера 1. Пусть теперь проценты начисляются два раза в год. Рента постнумерандо.
Имеем: j = 0,12 m = 2 R = 100 тыс. руб. n = 3 |
Решение: Так как рента годовая, постнумерандо, проценты начисляются два раза в год, то наращенная сумма определяется по формуле (1.4.): |
S=? |
|
|
|
26. Долговые ценные бумаги, их основные параметры, порядок расчетов, учет влияния инфляции. Понятие длительности портфеля облигаций.
27. Расчеты с процентными и дисконтными обязательствами. Особенности расчета комиссионных по соответствующим инструментам. Доходность финансовых инструментов и операций с учетом налогообложения. (вопрос )
28. Доходность финансовых инструментов и операций с учетом комиссионных, налогообложения и инфляции.(вопрос )
29. . Сходство и различия между простыми и сложными ставками процентов, область их применения в банковской практике. Длительность финансовых инструментов (дюрация) и ее использование в практической банковской деятельности.
30. Простые ставки процентов, основные понятия и формулы. Точные и обыкновенные проценты. Доходность финансовых операций в условиях инфляции (при использовании простых ставок процентов). Особенности расчетов при операциях с векселями.(Вопрос )
31. Основные подходы к учету инфляции в финансовых рентах. Влияние инфляции на обобщающие параметры рент.
32. Формула сложных процентов. Множитель наращения и способы его определения. Дисконтирование по формуле сложных процентов. Определение срока платежа и ставки процентов. Сравнение интенсивности процессов наращения и дисконтирования по различным видам ставок. (Вопрос )
![]()
![]()
![]()
![]()
![]()
Срок операции в днях
![]()
![]()
Срок операции в годах
![]()
![]() ;
;
![]() ;
;![]()
33. Сущность инфляции. Индекс и темп инфляции. Индексация ставки процентов. Брутто-ставка процентов. Формула Фишера. Индексация первоначальной суммы долгового обязательства.
Уравнение Фишера — уравнение, описывающее связь между темпом инфляции, номинальной и реальной ставками процента:
![]()
где i — номинальная ставка процента;
r — реальная ставка процента;
п — темп инфляции.
Уравнение показывает, что номинальная ставка процента может измениться по двум причинам:
из-за изменений реальной ставки процента;
из-за темпа инфляции.Например, если субъект положил на банковский счёт сумму денег, приносящую 10 % годовых ежегодно, то номинальная ставка составит 10 %. При уровне инфляции 6 % реальная ставка составит только 4 %.

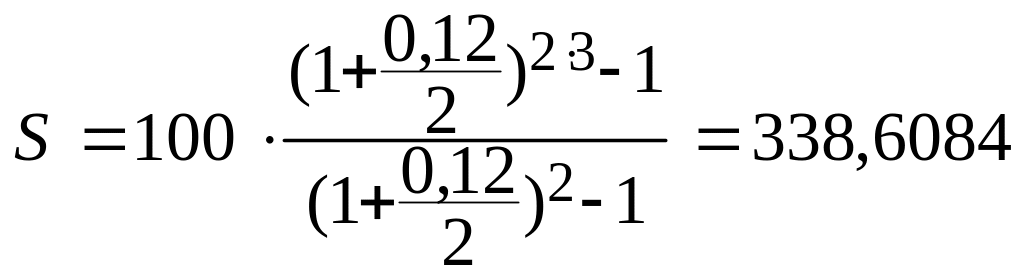 тыс.
руб.
тыс.
руб.