6. Дисконтирование, его сущность и виды. Расчеты с использованием простых ставок процентов и простых учетных ставок в условиях инфляции.

В финансовой практике часто сталкиваются с задачей обратной наращению процентов: по заданной сумме FV, которую следует уплатить через время n;

необходимо определить сумму получаемой ссуды P. Параметры операции: n– длительность финансовой операции (измеряется в годах),i–годовая ставка ссудного процента; d– учетная ставка (ставка дисконта)P-современная стоимость будущей суммы FV;

Виды дисконтирования:

а) по ставке простого процента:

Коэффициент дисконтирования

б) по учетной ставке

=1-dn

в) по ставке сложного процента с начислением один раз в году:

Коэффициент дисконтирования

г) по ставке сложного процента с начислением m раз в году:

Непосредственные расчеты в условиях инфляции:

1 тип: есть какой-то показатель, который нужно очистить от инфляции.

2 тип: мы имеем какой-то показатель о реальном выражении и пытаемся узнать, какая инфляция нам достичь этих показателей.

1) В условиях инфляции все показатели бывают неочищенные от инфляции или номинально брутто-показатели.

2)Очищенные от инфляции реальные или нетто-показатели, т.е. в реальном выражении.

Учет инфляции при начислении простых процентов.

Инфляция - снижение покупательской способности денег. Т.о. для расчета простой ставки процента в условиях инфляции необходимо рассмотреть индекс инфляции и уровень инфляции, а также наращенную сумму в условиях инфляции.

э то уровень инфляцииI_инф - индекс инфляции; S-это наращенная сумма в условиях инфляции

N - число периодов

В условиях инфляции ставка простых процентов также изменяется под влиянием уровня или индекса инфляции. Уровень инфляции за некоторый период времени показывает на сколько процентов вырастут цены. А индекс инфляции - во сколько раз вырастут цены.

Если указан годовой уровень инфляции, то простая ставка процентов, компенсирующая потери от инфляции, будет рассчитываться по следующей формуле:

г де r - ставка простых процентов до инфляции

это ставка простых процентов в условиях инфляции

Если срок будет дробным (в днях), то эту формулу можно записать следующим образом:

Т .о. уровень и индекс инфляции оказывает огромное, значительное влияние на расчеты простой ставки процентов и не погашаемую сумму вклада или ссуды, когда сумма процентных денег определяется исходя из первоначальной суммы и в зависимости от срока и ставки простых процентов.

Различают, как правило, ставки процентов и учетные ставки, как было сказано выше. При использовании простых ставок процентов все расчеты производятся исходя из первоначальной суммы с учетом срока и ставки процента. При использовании сложных ставок процентов сумма процентных денег на определенном этапе или периоде определяется исходя из первоначальной суммы "+" проценты, начисленные за предшествующие периоды (т.е. процент на процент). При использовании учетных ставок процентов процентные деньги издерживаются непосредственно при выдаче ссуды в виде дисконта, например, при учете векселей.

При использовании учетных ставок расчеты производятся исходя из конечной наращенной суммы.

Учет инфляции при использовании учетной ставки.

Рассмотрим производные показатели, исходя из основной формулы дисконтирования по учетной ставке:

1 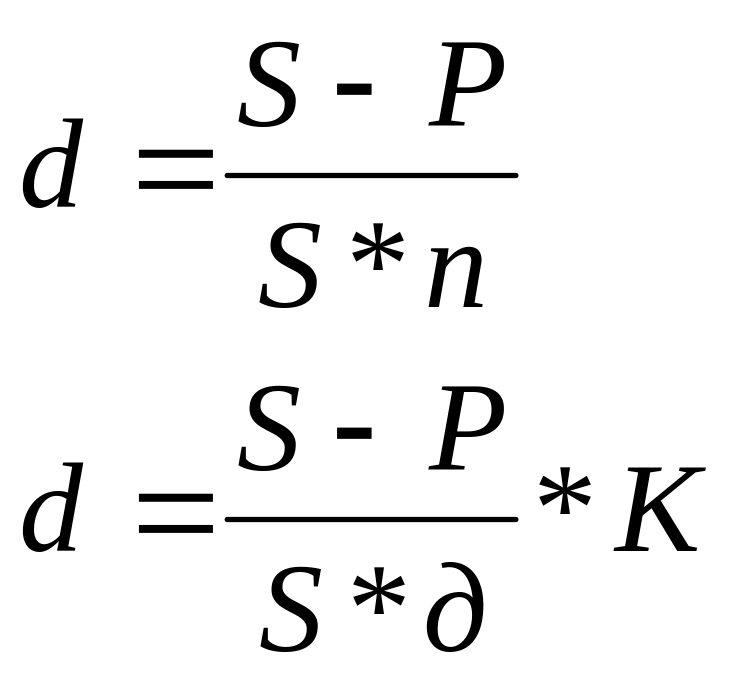). произведем математическое преобразование для определения срока в годах и днях:

2). определим размер учетной ставки в годах и в днях:

В условиях инфляции учетная ставка также может быть подвергнута влиянию индекса или уровня инфляции. Расчеты с использованием индекса инфляции за весь срок ссуды является общим для всех сроков ссуды. Пи этом не требуется знать, как меняется уровень инфляции в течение срока ссуды, т.е. чаще всего рассматривается индекс инфляции.

Е сли же задан годовой уровень инфляции, то учетная ставка, компенсирующая потери от инфляции, будет рассчитываться следующим образом:

7. Изменение условий контракта на основе уравнения эквивалентности платежей. Понятие потока платежей (финансовой ренты).

Современные финансово-банковские операции часто предполагают не отдельные или разовые платежи, а некоторую их последовательность во времени. Например, погашение задолженности в рассрочку, периодическое поступление доходов от инвестиций, накопление пенсионного фонда или выплата пенсий и т.д. Такую последовательность, или ряд платежей называют потоком платежей, а отдельный элемент этого ряда — членом потока.

Члены потока платежей могут быть как положительными (поступления), так и отрицательными величинами (выплаты).

Поток платежей, все члены которого положительные величины, а временные интервалы между платежами одинаковы, называют финансовой рентой или просто рентой, или аннуитетом, независимо от назначения или происхождения платежей. Например, рентой является последовательность получения процентов по облигациям, платежи по потребительскому кредиту, выплата в рассрочку страховых премий и т.п.

Во всех приведенных случаях выплата или получение денег производится через равные промежутки времени.