Лабораторна робота д11 Тема: Дослідження поступального та обертального рухів твердого тіла Завдання на лабораторну роботу д11

Механічна система складається з механізма (колес 1 і 2) і вантажу 3.

До колеса 1 прикладена пара сил з моментом М = М(t) або сила Р = Р(t), що рухає систему.

Час t відлічується від деякого момента (t=0), коли кутова швидкість колеса 1 дорівнює 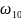. Момент сил опору ведомого колеса 2 дорівнює . Інші сили опору руху системи не враховувати.

Маси колес 1 і 2 дорівнюють m₁ і m₂, а маса вантажа 3 – m₃. Радіуси великих та малих кіл колес R₁, r₁, R₂, r₂.

Схеми механічних систем наведені на рис. 1 – 30, а необхідні для рішення дані – в таблиці Д11.

Знайти рівняння руху тіла системи, що вказане в останній графі таблиці і побудувати графік зміни швидкості (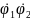 або 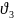) за проміжок часу від t=0 до t=t₁. Визначити також натяг ниток в заданий момент часу, а у варіантах, де має місце стикання коліс 1 і 2, знайти, крім цього, окружне зусилля в точці їх стикання. Колеса 1 і 2, для яких радіуси інерції i_х1 і і_х2 не задані, вважати цілковитими однорідними дисками.

Приклад виконання лабораторної роботи д11.

У даній механічній системі (див. схеми у звіті до лабораторної роботи) колеса 1 і 2 механізму обертаються навколо нерухомих осей, а вантаж 3 здійснює поступальний рух.

Запишемо диференціальні рівняння руху кожного з цих трьох тіл, для чого відділимо одне від одного, розрізавши нитку, що утримує вантаж 3, і роз´єднаємо колеса 1 і 2 у точках стикування зубців (див. розрахункову схему).

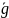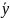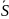До колеса 1 прикладена сила ваги m₁ , рушійний момент М, складові реакції підшипника _А, _А, окружне зусилля ₁ і нормальна реакція 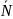₁ колеса 2.

До колеса 2 механізму прикладені сила ваги m₂ , момент сил опору М_с , складові реакції підшипника _b, _b, сила натягнення 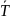нитки, до якої причеплений вантаж 3, окружне зусилля ₂ і нормальна реакція ₂ колеса 1.

До вантажа 3 прикладені сила ваги m₃ і натягнення нитки ₁.

Очевидно, що

₂ = − ₁, ₁ = − ₂, ₁ = − _.

Диференціальне рівняння обертального руху колеса 1 навколо осі х₁ складаємо у вигляді

I_{х1 1} = ,

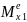де – головний момент зовнішніх сил, прикладених до колеса 1, відносно осі обертання х₁:

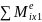= Μ – S₁R₁.

(Момент М приводить до руху колесо 1 і тому прийнятий додатним, а момент, що здійснюється окружним зусиллям ₁, перешкоджає обертанню колеса 1 і, таким чином, від´ємний).

Диференціальне рівняння обертального руху колеса 1 приймає вигляд:

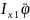₁ = Μ – S₁R₁. (1)

Складемо диференціальне рівняння обертального руху колеса 2 навколо осі х₂:

I_{х2 2} = ∑

або

I_{х2 2} = S₂R₂ − T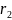 − 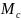. (2)

(Знаки моментів сил ₂, і моменту сил опору прийняті за тим же правилом, що і при складанні рівняння (1)).

Складемо диференціальне рівняння поступального руху вантажа 3:

m₃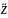 = ∑F ,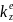

де проекція головного вектора зовнішніх сил, прикладених до вантажа 3, на вісь z, спрямовану у бік руху вантажа, тобто догори:

∑F = T₁ – m₃g

І, таким чином, маємо диференціальне рів неня у вигляді

m₃ = T₁ – m₃g.

В рівняннях (1), (2), (3) невідомими є сили T₁ = T, S₁ = S₂ = S, а також функції ₁(t), ₂(t) і (t) – кутові прискорення колес 1, 2 і прискорення вантажа 3відповідно. Але зазначені функції пов´язані між собою співвідношеннями

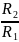= , (4)

= ₂r₂. (5)

Таким чином, із врахуванням (4) і (5) система рівнянь (1), (2), (3) може бути зведена до системи з трьома невідомими T, S і ₂, тобто розв´язується цілком алгебраїчно.

Числове вирішення наведено у прикладі звіту лабораторної роботи.

Визначити рівняння руху тіла системи, вказаного в останньому стовбчику таблиці вихідних даних.

Визначити також …