
- •Предмет теории вероятности. Основные задачи.
- •Понятие события, классификация
- •Классическое определение вероятности
- •Статистическое определение вероятности
- •Элементы комбинаторного анализа
- •Действия над событиями.
- •Теорема сложения вероятностей несовместных событий
- •Условная вероятность. Теорема умножения вероятностей. Независимые события.
- •Теорема сложения вер-тей совместных событий
- •Формула полной вероятности. Формула Байеса
- •Повторные независимые испытания. Формула Бернулли
- •Приближенные вычисления вероятностей в схеме испытаний Бернулли
- •Случайные величины. Закон распределение дискретной случайной величины
- •Математические операции над дсв
- •Математическое ожидание дсв
- •Математическое ожидание числа появлений события в нез. Исп.
- •Дисперсия дсв
- •Дисперсия числа появлений события в независимых испытаниях
- •Основные законы распределения дсв
- •Распределение Пуассона
- •Гипергеометрическое распределение
- •Функция распределения вероятностей случайной величины
- •График функции распределения дсв
- •Непрерывные случайные величины. График.
- •Теорема о вер-ти отдельно взятого значения нсв
- •Вероятность попадания нсв в заданный интервал
- •Плотность вероятности нсв
- •Нахождение функций по плотности распределения
- •Числовые характеристики случайных величин
- •Равномерный закон распределения нсв
- •Показательный закон распределения нсв
- •Нормальный закон распределения нсв
- •Нормальная кривая. Влияние параметров на ее форму.
- •Свойства случайной величины, распределенной по нормальному закону.
- •Закон больших чисел
- •Основные задачи математической статики
- •Сплошное и выборочное наблюдения. Генеральная и выборочная совокупности. Типы выборок. Репрезентативность.
- •Статистическое распределение выборки. Эмпирическая функция распределения. Полигон и гистограмма.
- •Оценка параметров генеральной совокупности. Свойства оценок.
- •Основные методы нахождения оценок.
- •Точечные оценки параметров генеральной совокупности по собственно-случайной выборке.
- •Интервальное оценивание. Предельная ошибка выборки.
Дисперсия числа появлений события в независимых испытаниях
Эксперимент повторяется n раз, А- событие.
Р(А)=р
Р(неА)=q=1-p
X-число появлений события А в n-независимых испытаниях.
М(Х)=np
D(X)=?
Теорема: дисперсия числа появления события n-независимых испытаний равно npq.
D(X)=npq, где р- вероятность появления события;р=Р(А);q=Р(неА)
Док – во:
Х=Х1+Х2+…+Хn ,где Xi- появление (непоявление) события А(i изменяется от 1 до n) в конкретном i-том эксперименте.
Хi 0 1
P q p
D(X)=D(X1)+D(X2)+…+D(Xn)
M(X12)= 0*q+1*p=p
D(X1)=M(X12)-(M(X1))2=p-p2=p(1-p)=pq=>D(X)=npq
Основные законы распределения дсв
Биномиальным называют закон распределения Д.С.В. Х - числа появлений события в n независимых испытаниях, в каждом из которых вероятность появления события равна р, вер-ть возможного значения Х=k (числа k появлений события) вычисляют по формуле Бернулли: Pn (k)=Cn^k* p^k *q^(n-k)
Распределение Пуассона
Говорят,
что случайная величина
![]() имеет
распределение Пуассона
с параметром
имеет
распределение Пуассона
с параметром
![]() ,
где
,
где
![]() ,
и пишут:
,
и пишут:
![]() ,
если
принимает
значения
,
если
принимает
значения
![]() с
вероятностями
с
вероятностями
![]() .
Таблицу распределения
читатель
может нарисовать самостоятельно.
.
Таблицу распределения
читатель
может нарисовать самостоятельно.
Гипергеометрическое распределение
Говорят,
что случайная величина
имеет
гипергеометрическое
распределение с
параметрами
,
и
,
где
![]() ,
,
![]() ,
если
принимает
целые значения
такие,
что
,
если
принимает
целые значения
такие,
что
![]() ,
,
![]() ,
с
вероятностями
,
с
вероятностями
![]() .
Случайная величина с таким распределением
имеет смысл числа белых
шаров среди
шаров,
выбранных наудачу и без возвращения из
урны, содержащей
белых
шаров и
не
белых.
.
Случайная величина с таким распределением
имеет смысл числа белых
шаров среди
шаров,
выбранных наудачу и без возвращения из
урны, содержащей
белых
шаров и
не
белых.
Функция распределения вероятностей случайной величины
Описание
распределения
набором вероятностей
![]() не
очень удобно: слишком много существует
борелевских множеств. Мы описали
дискретные
распределения
таблицей распределения, абсолютно
непрерывные —
плотностью распределения. Попробуем
поискать какой-нибудь универсальный
способ описать любое возможное
распределение.
не
очень удобно: слишком много существует
борелевских множеств. Мы описали
дискретные
распределения
таблицей распределения, абсолютно
непрерывные —
плотностью распределения. Попробуем
поискать какой-нибудь универсальный
способ описать любое возможное
распределение.
Можно
поставить вопрос иначе: распределение
есть набор вероятностей попадания в
любые борелевские
множества
на прямой. Нельзя ли обойтись знанием
вероятностей попадания в какой-нибудь
меньший набор множеств на прямой?
Борелевская
![]() -алгебра
-алгебра
![]() порождается
интервалами
(равно как и лучами
порождается
интервалами
(равно как и лучами
![]() ),
поэтому можно ограничиться только
вероятностями попадания в такие лучи
для всех
),
поэтому можно ограничиться только
вероятностями попадания в такие лучи
для всех
![]() .
А уже с их помощью можно будет определить
и вероятность попасть в любое борелевское
множество.
.
А уже с их помощью можно будет определить
и вероятность попасть в любое борелевское
множество.
Замечание.
Можно
с таким же успехом ограничиться набором
вероятностей попадания в интервалы
![]() ,
или в
,
или в
![]() ,
или в
,
или в
![]() .
.
Определение.
Функцией
распределения
случайной величины
называется
функция
![]() ,
при каждом
равная
вероятности случайной величине
принимать
значения, меньшие
,
при каждом
равная
вероятности случайной величине
принимать
значения, меньшие ![]() :
:
![]()
Перечислим основные дискретные и абсолютно непрерывные распределения и найдём их функции распределения.
Если функция распределения F (x) непрерывна, то случайная величина называется непрерывной случайной величиной.
Если функция распределения непрерывной случайной величины дифференцируема, то более наглядное представление о случайной величине дает плотность вероятности случайной величины p (x), которая связана с функцией распределения F (x) формулами
 и
и
![]() .
.
Отсюда,
в частности, следует, что для любой
случайной величины
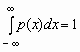 .
.
