
- •Правила выполнения и оформления контрольных работ
- •Студент должен выполнять вариант, номер которого совпадает с цифрой его шифра (номера зачетной книжки), если последняя цифра 0, то решают задачи с 10, 20…
- •Контрольная работа №II(1) Функции многих переменных. Неопределенный интеграл. Определенный интеграл, его приложения.
- •Контрольная работа №II(2) Кратные и криволинейные интегралы.
Контрольная работа №II(1) Функции многих переменных. Неопределенный интеграл. Определенный интеграл, его приложения.
1.
Дана функция
![]() .
Показать, что
.
Показать, что
![]() .
.
2.
Дана функция
![]() .
Показать, что
.
Показать, что
![]() .
.
3.
Дана функция z=ln(x2+y2+2x+1).
Показать, что
![]() .
.
4.
Дана функция
![]() .
Показать, что
.
Показать, что
![]() .
.
5.
Дана функция
![]() .
Показать, что
.
Показать, что
![]() .
.
6.
Дана функция
![]() .
Показать, что
.
Показать, что
![]() .
.
7.
Дана функция
z=![]() .
Показать, что
.
Показать, что
![]() .
.
8.
Дана функция![]()
![]() .
Показать, что
.
Показать, что
![]() .
.
9.
Дана функция z=sin(x+ay). Показать, что
![]() .
.
10.
Дана функция![]() .
Показать, что
.
Показать, что
![]()
11-20. Даны функция z=(x ; y), точка А(x0 ;y0) и вектор а. Найти: 1) grad z в точке А; 2) производную в точке А по направлению вектора а.
11. z = x2 + xy + y2 ; A(1 ; 1), a = 2i - j .
12. z = 2x2 + 3 xy + y2 ; A(2 ; 1), a = 3i - 4 j .
13. z = ln (x2 + 3y2); A(1 ; 1), a = 3i + 2j .
14. z = ln (5x2 + 4y2); A(1 ; 1), a = 2i - j .
15. z = 5x2 + 6 xy ; A(2 ; 1), a = i + 2j .
16. z = arctg (xy2); A(2 ; 3), a = 4i - 3j .
17.
z = arcsin
![]() ; A(1 ; 2), a
= 5i
- 12j
.
; A(1 ; 2), a
= 5i
- 12j
.
18. z = ln (3x2 + 4y2); A(1 ; 3), a = 2i - j .
19. z = 3x4 + 2x2y3 ; A(- 1 ; 2), a = 4i - 3j .
20. z = 3x2y2 + 5y2x ; A(1 ; 1), a = 2i + j .
21-30. Найти неопределенные интегралы. В первом примере результат проверить дифференцированием.
21.
a)
![]() ;
б)
;
б)
![]() ;
;
22.
a)
![]() ; б)
; б)
![]() ;
;
23.
a)
![]() ; б)
; б)
![]() ;
;
24.
a)
![]() ;
б)
;
б)
![]() ;
;
25.
a)
![]() ; б)
; б)
![]() ;
;
26.
а)![]() ;
б)
;
б)
![]() ;
;
27.
a)![]() ;
б)
;
б)
![]() ;
;
28.
a)
![]() ; б)
; б)
![]() ;
;
29.
a)
![]() ;
б)
;
б)
![]() ;
;
30.
a)
![]() ;
б)
;
б)
![]() ;
;
31-40. Вычислить несобственный интеграл или доказать его расходимость.
31.
![]() .
32.
.
32.
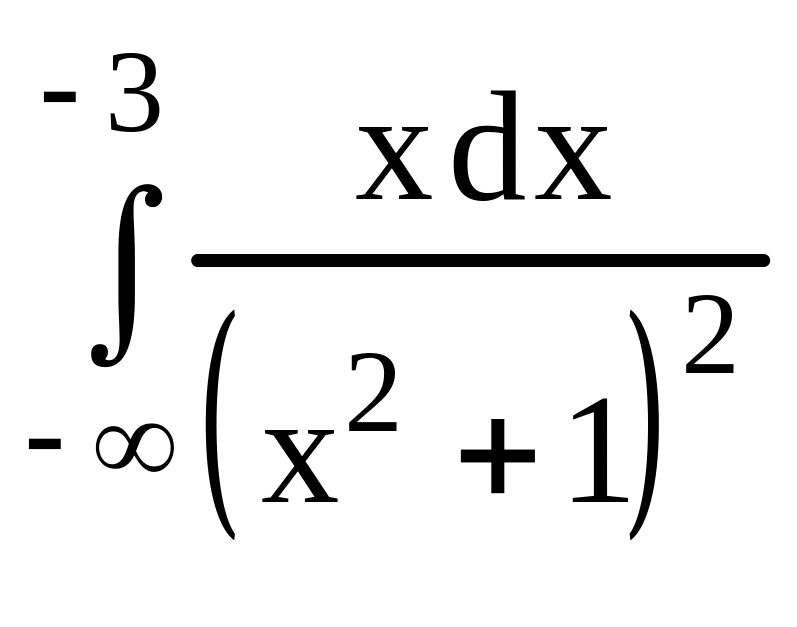 .
.
33.
![]() .
34.
.
34.
![]() .
.
35.
![]() .
36.
.
36.
![]() .
.
37.
![]() . 38.
. 38.
![]() .
.
39.
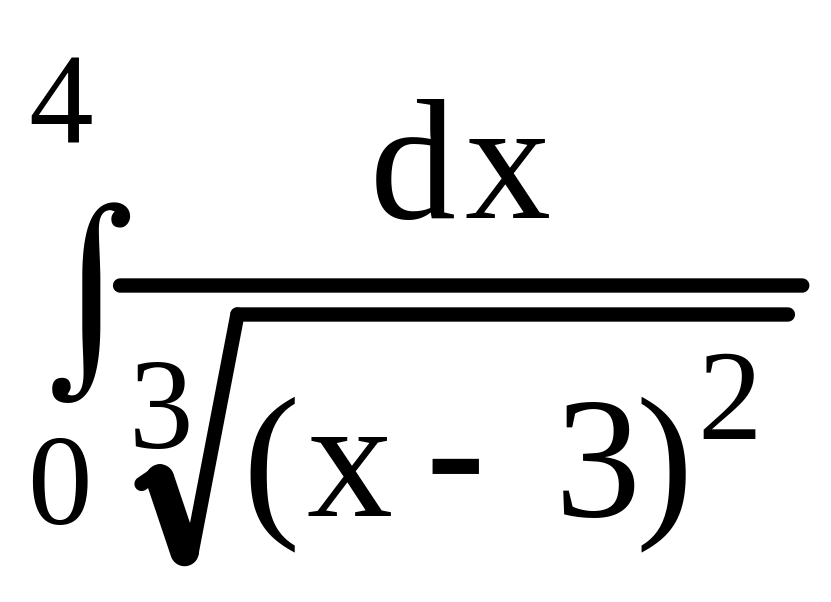 .
40.
.
40.
![]() .
.
Контрольная работа №II(2) Кратные и криволинейные интегралы.
41-50. Вычислить указанные двойные интегралы и изменить порядок интегрирования.
41.
![]() ,
где область D: 1 £
x £
2; y = 1; y = x.
,
где область D: 1 £
x £
2; y = 1; y = x.
42.
![]() ,
где область D: x+ y £
1, x -
y £
1, x ³
0.
,
где область D: x+ y £
1, x -
y £
1, x ³
0.
43.
![]() ,
где область D: y £
,
где область D: y £
![]() ,
y ³
0, x ³
0, x £
1.
,
y ³
0, x ³
0, x £
1.
44.
![]() ,
где область D: x ³
0; x £
,
где область D: x ³
0; x £
![]() ;
y £
sin x; y ³
0.
;
y £
sin x; y ³
0.
45.
![]() ,
где область D: y ³
x; y £
2x; x+ y £
6.
,
где область D: y ³
x; y £
2x; x+ y £
6.
46.
![]() ,
где область D: 0 £
y £
1; x= y; x =
,
где область D: 0 £
y £
1; x= y; x =
![]() .
.
47.
![]() dx dy, где область D: x = 2; y = x; xy = 1.
dx dy, где область D: x = 2; y = x; xy = 1.
48.
![]() dx dy, где область D: x = 0; y = p;
y = x.
dx dy, где область D: x = 0; y = p;
y = x.
49.
![]() dx
dy, где область D: y = x2
; y2
= x.
dx
dy, где область D: y = x2
; y2
= x.
50.
![]() ,
где область D: y = 1; y = 2; x = 0; y =
.
,
где область D: y = 1; y = 2; x = 0; y =
.
51 - 60. Вычислить объем тела, ограниченного указанными поверхностями. Сделать чертежи данного тела и его проекции на плоскость ХОУ.
51. z = 0, 4z = y2 , 2x - y = 0, x + y = 9.
52. z = 0, z = 4 , x = 0, x + y = 4.
53. z = 0, z = x2 , 3x + 2y =6, y = 0.
54. z = 0, z = 2 x2 +3y2, x + y = 1, x = 0, y = 0.
55. z = 0, z = y2 , y = 2x, x = 1.
56. z = 0, y = x2 , z = y, z = 6.
57. z = 0, z = y2 , 2x + 3y = 6, x = 0.
58.
z = 0, y =
![]() ,
z = 5x.
,
z = 5x.
59. z = 0, z = x2 + y2 , y = x2 , y = 1.
60. y = 0, z = 0, 3x + y = 6, 3x + 2y = 12, x + y + z = 6.
61.
Вычислить криволинейный интеграл
![]()
![]() ds,
вдоль первой арки циклоиды
ds,
вдоль первой арки циклоиды
![]()
62.
Вычислить криволинейный
интеграл
![]() ,
,
где L - парабола y = x2 (0 £ x £ 2).
63.
Вычислить криволинейный
интеграл
![]() x dy,
x dy,
вдоль дуги y = ln x от точки А(1; 0) до точки В(е; 1).
64.
Вычислить криволинейный
интеграл
![]() -
(y2
+ x),
-
(y2
+ x),
где L - треугольник АОВ. { A( 3; 0), B (2; 1), O(0; 0)}.
65.
Вычислить криволинейный
интеграл
![]() ,
,
вдоль L дуги параболы у = х2 от точки А(1; 1) до точки В(2; 4).
66. Вычислить криволинейный интеграл
![]() ,
,
вдоль верхней половины L эллипса x = 3 cos t, y = 2 sin t
(0 £ t £ p).
67.
Вычислить криволинейный
интеграл
![]() ,
вдоль дуги L окружности
,
вдоль дуги L окружности
![]() .
.
68.
Вычислить криволинейный интеграл![]() ,
вдоль дуги L параболы у =
,
вдоль дуги L параболы у =
![]() от точки А ( 1;
от точки А ( 1;
![]() )
до точки В( 2; 2).
)
до точки В( 2; 2).
69.
Вычислить криволинейный
интеграл
![]() ,
вдоль отрезка L = AB прямой от точки А(1;
2) до точки В(2; 4).
,
вдоль отрезка L = AB прямой от точки А(1;
2) до точки В(2; 4).
70.
Вычислить криволинейный
интеграл
![]() ,
вдоль границы L треугольника АВС, обходя
ее против часовой стрелки, если А(1; 0),
В(1; 1), С (0; 1).
,
вдоль границы L треугольника АВС, обходя
ее против часовой стрелки, если А(1; 0),
В(1; 1), С (0; 1).
71 -80. Преобразовать криволинейный интеграл в двойной и вычислить его ( по формуле Грина).
71.
![]() ,
где С -
контур области, ограниченной линиями:
y = x, y = 2x -
x2
.
,
где С -
контур области, ограниченной линиями:
y = x, y = 2x -
x2
.
72.
![]() ,
где С: у = 2 -
х2
, у = х2
.
,
где С: у = 2 -
х2
, у = х2
.
73.
![]() где С: xy = 1, y = 2, x = 2.
где С: xy = 1, y = 2, x = 2.
74.
![]() где С: y=
где С: y=![]() ,
y = x, y = 0.
,
y = x, y = 0.
75.
![]() где С: x =1, y2
= x.
где С: x =1, y2
= x.
76.
![]() где С: x+y = 2, x=0, y= 0.
где С: x+y = 2, x=0, y= 0.
77.
![]() где С - контур треугольника АВС: A(1; 1),
B(3; 2), C(2; 5).
где С - контур треугольника АВС: A(1; 1),
B(3; 2), C(2; 5).
78.
![]() где С: x2 +
y2
= 2y.
где С: x2 +
y2
= 2y.
79.![]() где С: 6y+ x £
4, x ³
-
4 -y2,
y ³
0.
где С: 6y+ x £
4, x ³
-
4 -y2,
y ³
0.
80.
![]() где С: y = 3x2,
y = 2x.
где С: y = 3x2,
y = 2x.
