Лабораторная работа № 2

УТОЧНЕНИЕ ПРИБЛИЖЕННОГО КОРНЯ УРАВНЕНИЯ

МЕТОДОМ ХОРД, МЕТОДОМ КАСАТЕЛЬНЫХ (НЬЮТОНА), МОДИФИЦИРОВАННЫМ МЕТОДОМ НЬЮТОНА,

МЕТОДОМ СЕКУЩИХ, КОМБИНИРОВАННЫМ МЕТОДОМ

Цель работы: изучить численные методы уточнения корней уравнений: метод хорд, метод касательных, модифицированный метод касательных, метод секущих, комбинированный метод; вычислить предложенными методами с точностью до действительный корень заданного алгебраического уравнения .

Постановка задачи

1. Отделить корни для заданного алгебраического уравнения . Для решения этой задачи использовать графический метод.

2. Решить задачу уточнения корня, используя комбинированный метод (ручной счет).

3. Решить задачу уточнения корней уравнения с заданной точностью , используя метод хорд, метод касательных, модифицированный метод касательных, метод секущих, комбинированный метод в пакете МATHCAD, записав соответствующие программные блоки.

4. Решить задачу уточнения корней предложенными методами с заданной точностью в среде MATLAB.

5. Проверить правильность результатов с помощью встроенных функций пакетов.

6. Свести все полученные результаты в таблицу, сделать выводы о скорости сходимости использованных методов, оценить погрешность результата, используя теорему о погрешности приближенного корня.

Содержание отчета

1. Постановка задачи.

2. Теоретические сведения: расчетные формулы и геометрическая интерпретация для каждого метода.

3. Три-четыре итерации комбинированного метода для заданного уравнения (ручной счет).

4. Результаты счета на ЭВМ.

5. Выводы.

Теоретические сведения

1. Метод линейной интерполяции (метод хорд). Пусть дано уравнение , где функция непрерывна на [a;b] и f(a)f(b)<0. Для определенности положим f(a)>0 и f(b)<0. Тогда, вместо того чтобы делить отрезок [a;b] пополам (как это делается в методе половинного деления), более естественно поделить его в отношении f(a)/f(b). Это дает приближенное значение корня x₁=b+h₁, где

Далее, применив этот прием к тому из отрезков ([a;x₁] или [x₁;b]), на концах которого функция f(x) имеет противоположные знаки, получим второе приближение корня x₂ и т.д.

Геометрически способ пропорциональных частей эквивалентен замене кривой y = f(x) хордой, проходящей через точки A(a;f(a)) и B(b;f(b)) ( рис. 2.1).

Рис. 2.1. Геометрическая интерпретация метода хорд

В самом деле, уравнение хорды AB есть .

Отсюда, полагая x=x₁ и y=0, получаем .

Для сходимости метода хорд необходимо, чтобы выполнялись следующие условия:

а) неподвижен тот конец хорды, для которого знак функции f(x) совпадает со знаком ее второй производной f”(x);

б) последовательные приближения x_n лежат по ту сторону корня ξ, где функция f(x) имеет знак, противоположный знаку ее второй производной f”(x).

Расчетная формула метода в случае неподвижной точки a:

.

Если отрезок [a;b] достаточно мал, то погрешность метода определяется так:

.

Таким образом, в этом случае, как только будет выполняться условие , где ε – заданная предельная абсолютная погрешность, гарантировано, что .

2. Метод Ньютона (метод касательных). Пусть – корень уравнения – отделен на отрезке [a, b], причем и непрерывны и сохраняют определенные знаки при .

Положим , где считаем малой величиной. Отсюда, применив формулу Тейлора, получим

0 = .

Следовательно,

.

Внеся эту поправку в формулу уточнения корня, можно найти следующее (по порядку) приближение корня:

( n = 0, 1, 2, . . .).

Геометрически метод Ньютона эквивалентен замене небольшой дуги кривой y = f(x) касательной, проведённой в некоторой точке кривой (рис. 2.2).

Рис. 2.2. Геометрическая интерпретация метода Ньютона

Теорема. Если , причем и отличны от нуля и сохраняют определенные знаки при , то, исходя из начального приближения , удовлетворяющего неравенству , можно вычислить методом Ньютона

единственный корень уравнения с любой степенью точности.

Применяя метод Ньютона, следует руководствоваться следующим правилом: в качестве исходной точки выбирается тот конец интервала , которому отвечает ордината того же знака, что и знак .

Условием завершения итерационного процесса является выполнение неравенства , где ε – заданная предельная абсолютная погрешность.

3. Модифицированный метод Ньютона. Если производная f’(x) мало изменяется на отрезке [a, b], то в расчетной формуле метода касательных можно положить ≈ .

Отсюда для корня уравнения f(x) = 0 получаем последовательные приближения

( n = 0, 1, 2, . . .).

Геометрически этот способ означает, что заменяются касательные в точках B_n[x_n, f(x_n)] прямыми, параллельными касательной к кривой y = f(x), в её фиксированной точке B₀[x₀, f(x₀)] (рис. 2.3). Эта формула весьма полезна, если сложна.

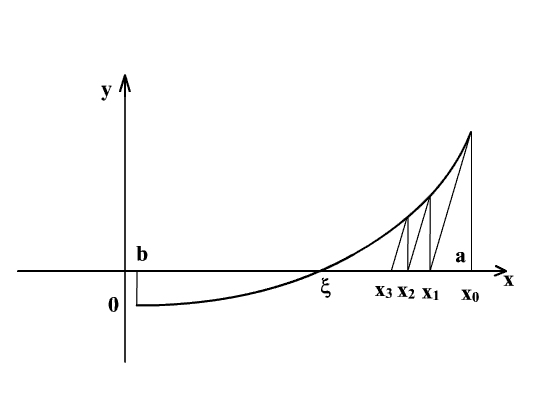
Рис. 2.3. Геометрическая интерпретация модифицированного

метода Ньютона

4. Метод секущих. В алгоритме Ньютона требуется вычислить две функции для каждой итерации – и . Метод секущих требует только одного вычисления функции при одной итерации, и простой корень имеет порядок сходимости R 1,618033989. Этот метод почти так же быстр, как и метод Ньютона, который имеет порядок сходимости R=2.

В методе секущих используется такая же формула, как и в методе хорд, но существуют различные логические решения относительно способа поиска каждого последующего члена. Необходимо около точки иметь две начальные точки и , как показано на рис. 2.4. Определим как абсциссу точки пересечения линии, проходящей через эти две точки, и оси 0X. Тогда на рис. 2.4 видно, что будет ближе к корню , чем или .

Рис. 2.4. Геометрическая интерпретация метода секущих

Уравнение, связывающее и , находим, рассматривая тангенс угла наклона

и .

Значения m в формуле равны тангенсу угла наклона секущей, которая проходит через два первых приближения к тангенсу угла наклона прямой, проходящей через точки и (x₂; 0) соответственно. Приравняем правые части, решим относительно .

Общий член, определенный согласно двухточечной итерационной формуле:

Условие завершения процесса приближений такое же, как и в методе Ньютона.

5. Комбинированный метод. Метод, используемый для вычисления значения корня с заданной точностью, заключается в поочередном применении метода хорд и метода касательных. Концы отрезка, содержащего корень уравнения, обозначим и . Условимся обозначать через тот конец отрезка, на котором знаки функции и её второй производной совпадают. Через точки , проведём хорду. Точку пересечения хорды с осью обозначим через . В точке проведём касательную к кривой . Точку пересечения касательной с осью обозначим через . Итак, получен новый отрезок с концами и , содержащий корень уравнения (рис. 2.5). Аналогично получаем отрезок с концами , и т.д.

Рис. 2.5. Геометрическая интепретация комбинированного метода

Расчётные формулы комбинированного метода для случая, приведенного на рис. 2.5, имеют следующий вид:

, ;

, ,

где .

Если корень уравнения требуется вычислить с точностью до , то процесс вычисления корня можно прекращать в тот момент, когда . В качестве ответа взять среднее арифметическое последних полученных значений и , т.е. .

Погрешность численного решения уравнения. Для оценки точности приближения можно воспользоваться формулой

,

Приведем еще формулу, позволяющую оценивать абсолютную погрешность приближенного значения , если известны два последовательных приближения и . Будем предполагать, что производная непрерывна на отрезке , содержащем все приближения, и сохраняет постоянный знак, причем

.

Примем для определенности, что последовательные приближения точного корня вычисляются по формуле

(n = 1,2,…),

где конец является неподвижным. Отсюда будем иметь

.

Применив теорему Лагранжа о конечном приращении функции, получим

,

где и . Следовательно

(2.1)

Поскольку сохраняет постоянный знак на отрезке , причем и , то, очевидно, имеем

Из выражения (2.1) выводим формулу

, (2.2)

где за могут быть взяты соответственно наименьшее и наибольшее значения модуля производной на отрезке . Если отрезок столь узок, что имеет место неравенство то из формулы (2.2) получаем .

Таким образом, в этом случае, как только будет выполняться условие

,

где – заданная предельная абсолютная погрешность, гарантировано, что .