ЛАБОРАТОРНАЯ РАБОТА (СМО)

1. Понятие «потока событий».

При рассмотрении случайных процессов, протекающих в системах с дискретными состояниями и непрерывным временем, часто приходит­ся встречаться с так называемыми «потоками событий».

Потоком событий называется последовательность одно­родных событий, следующих одно за другим в случайные моменты времени.

Будем изображать поток событий последовательностью точек на оси времени Ot (рис. 1). при этом положение каждой точки на оси абсцисс случайно.

Рис.1

1. Поток событий называется стационарным, если вероят­ность попадания того или иного числа событий на участок времени длиной t (рис. 1) зависит только от длины участка и не зави­сит от того, где именно на оси Ot расположен этот участок.

2. Поток событий называется потоком без поcледействия, если для любых непересекающихся участков времени число событий, попадающих на один из них, не зависит от того, сколько со­бытий попало на другой (или другие, если рассматривается больше двух участков).

3. Поток событий называется ординарным, если вероятность попадания на элементарный участок двух или более событий пренебре­жимо мала по сравнению с вероятностью попадания одного события.

Поток событий, обладающий всеми тремя свойствами (стационарностью, отсутствием последействия, ординарностью) назы­вается простейшим (или стационарным пуассоновским) потоком. Название «простейший» связано с тем, что математическое описание со­бытий, связанных с простейшими потоками, оказывается наиболее простым.

Особенностью простейшего потока собы­тий является то, что промежуток времени Т между сосед­ними событиями в простейшем потоке распределен по показательному закону; его среднее значение и среднее квадратическое отклонение равны , где - интенсивность потока.

Для нестационарного пуассоновского потока закон распределе­ния промежутка Т уже не будет показательным; вид этого закона будет зависеть, во-первых, от того, где на оси Ot расположено первое из со­бытий, и, во-вторых, от вида зависимости , характеризующей пере­менную интенсивность потока. Однако если меняется сравнитель­но медленно и его изменение за время между двумя событиями невели­ко, то закон распределения промежутка времени между событиями мож­но приближенно считать показательным (или экспоненциальным) вида (1), полагая в этой формуле величину , равной среднему значению на том участке, который нас интересует.

(t>0), (1)

где - плотность распределения случайной величины Т.

2. Понятие «системы массового обслуживания».

При исследовании случайных процессов очень часто приходится сталкивать­ся с анализом работы своеобразных систем, называемых система­ми массового обслуживания (СМО). Примерами таких систем могут служить: телефонные станции, ремонтные мастерские, аэродромы, вокзалы и т. п.

Каждая СМО состоит из какого-то числа обслуживающих единиц, которые мы будем называть каналами обслуживания. В качестве «каналов» могут фигурировать: линии связи, рабочие точки, приборы, взлетно-посадочные полосы и т. д.

Системы массового обслуживания могут быть одноканальными или многоканальными.

Каждая СМО предназначена для обслуживания (выполнения) какого-то потока заявок (или «требований»), поступающих на СМО в случайные моменты времени. Об­служивание поступившей заявки продолжается некоторое случайное время, после чего канал освобождается и готов к при­нятию следующей заявки. Случайный характер потока заявок приво­дит к тому, что в какие-то промежутки времени на входе СМО скапли­вается излишне большое число заявок (они либо образуют очередь, либо покидают СМО необслуженными); в другие же периоды СМО будет работать с недогрузкой или вообще простаивать.

Каждая система массового обслуживания, в зависимости от числа каналов и их производительности, а также от характера потока заявок, обладает какой-то пропускной способностью, позво­ляющей ей более или менее успешно справляться с потоком заявок.

В качестве характеристик эффективности обслуживания, в зави­симости от условий задачи и целей исследования, могут применяться различные величины и функции, например:

— среднее количество заявок, которое может обслужить СМО в единицу времени;

— средний процент заявок, получающих отказ и покидающих СМО необслуженными;

— вероятность того, что поступившая заявка немедленно будет принята к обслуживанию;

— среднее время ожидания в очереди;

— закон распределения времени ожидания;

— среднее количество заявок, находящихся в очереди;

— закон распределения числа заявок в очереди;

— средний доход, приносимый СМО в единицу времени и т. д.

Случайный характер потока заявок, а в общем случае и длитель­ности обслуживания приводит к тому, что в системе массового обслужи­вания будет происходить какой-то случайный процесс

Для описания таких процессов в ряде случаев может быть с успе­хом применена схема марковского случайного процесса с дискретны­ми состояниями и непрерывным временем, который мы будем для крат­кости называть непрерывной цепью Маркова (рис.2). На рис.2 изображен размеченный граф состояний СМО, где - возможные состояния системы, - интенсивность потока событий.

Вероятности нахождения СМО в каждом состоянии в момент времени Т можно описать системой линейных дифференциальных уравнений Колмогорова:

, j=1,2,…,N. (2)

Для того, чтобы найти решение системы (2), нужно задать начальные условия Рі(0).

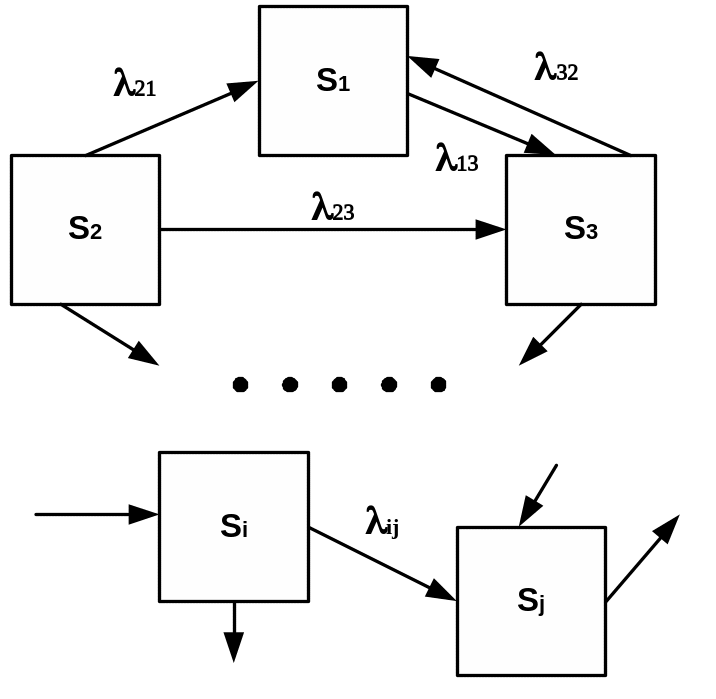
Рис.2

Уравнения Колмогорова строятся по вполне определенному правилу, которое можно сформулировать следующим образом.

В левой части каждого уравнения стоит производная вероятности состояния, а правая часть содержит столько членов, сколько стрелок связано с данным состоянием. Если стрелка направлена из состояния, соответствующий член имеет знак «минус»; если в состояние - знак «плюс». Каждый член равен произведению интенсивности перехода СМО из одного состояния в другое, соответс­твующей данной стрелке, умноженной на ве­роятность того состояния, из которого ис­ходит стрелка.

Это правило составления дифферен­циальных уравнений для вероятностей со­стояний является общим и справедливо для любой непрерывной марковской цепи; с его помощью можно совершенно механически, без всяких рассуждений, записывать диффе­ренциальные уравнения для вероятностей со­стояний непосредственно по размеченному графу состояний.