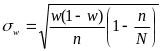Тема 6. Доверительный интервал. Критерий Пирсона

Литература

Забейворота В.И., Волохова К.И. Математика в экономике (Элементы математической статистики). Учебное пособие (параграф 12). УрСЭИ, Челябинск, 2001

Следует обратить внимание на суть интервального оценивания параметров распределения, на связь между доверительной вероятностью и доверительным интервалом.

Важно разобраться с тем, как находятся доверительные интервалы для оценки математического ожидания признаков, распределенных по нормальному закону.

При проверке гипотез необходимо уяснить смысл и роль таких понятий, как уровень значимости, критическая область, мощность критерия, причем в их взаимосвязи.

Безусловно, надо четко представлять общую схему статистической проверки гипотез.

Доверительным интервалом называется интервал (q^*-d;q^*+d), покрывающий параметр q с заданной надежностью g, где q^*- точечная оценка параметра q, d-точность оценки и Р(|q^* - q|<d)=g.

• Доверительный интервал для математического ожидания a нормально

распределенного количественного признака Х по выборочной средней

при известном s равен:

,

где t находим из равенства Ф(t)= по таблице 2 приложения;

при неизвестном s равен:

,

где S=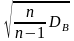 и tg находим по таблице 3 приложения tg=t(g,n).

• Доверительный интервал для среднего квадратического отклонения s

нормально распределенного количественного признака Х по исправленному равен:

(S(1-q); S(1+q)) при q<1 и (0; S(1+q)) при q³1,

где q находим по таблице 4 приложения q=q(g,n).

• Доверительный интервал неизвестной вероятности р биноминального распределения по относительной частоте w

,

где n–число испытаний, m–число появлений события, t находим из равенства Ф(t)= по таблице 2 приложения.

Замечание. При больших значениях n (порядка сотен) за доверительный интервал можно принять интервал равный

.

• Предельную ошибку d при нахождении доверительного интервала для математического ожидания m_x и для генеральной доли р можно вычислять по одной из формул таблицы

	Выборка
d=t×	Повторная	Бесповторная
для mx
для p

где t находим из равенства Ф(t)= по таблице 2 приложения.

• Объем выборки n при фиксированных предельной ошибке d и доверительной вероятности g можно вычислить по одной из формул следующей таблицы

Выборка Выборка	Повторная	Бесповторная
для mx
для p

где t находим из равенства Ф(t)= по таблице 2 приложения.

3Пример 9. В партии из 3000 изделий проверено 12 изделий. Среди них оказалось 3 бракованных изделия.

• Найти доверительную вероятность того, что доля брака во всей партии отличается от доли в выборке не более чем на 2%.

• Найти доверительный интервал, в котором с вероятностью 0,95 заключена доля брака во всей партии.

• Определить объем выборки, необходимый для того, чтобы с вероятностью 0,95 доля брака во всей партии отличалась от доли в выборке не более чем на 2%.

Решение.

• В качестве точечной оценки доли брака р во всей партии возьмем относительную частоту w=m/n=3/12=0,25.

Т.к. N=3000 велико по сравнению с n=12, то

Найдем доверительную вероятность того, что доля брака во всей партии отличается от доли в выборке не более чем на 2%.

Для этого потребуем, чтобы P(|w-p|£d)=2Ф(d/s_w)

Имеем d=0,02 и

(

где Ф(0,16)=0,0636 найдено по таблице 2 значений функции Лапласа приложения.

• Доверительный интервал для р при больших N имеет вид

.

Имеем и 2Ф(t)=0,95. Следовательно, Ф(t)=0,475 и по таблице 2 приложения t=1,96.

Итак, N=3000, w=0,25; t=1,96; n=12. Cледовательно, искомый доверительный интервал равен

(0,25-1,96× 0,25+1,96× =(0,005; 0,495)

• Чтобы найти необходимый объем выборки, воспользуемся формулой

n_w= .

Т.к. 2Ф(t)=g, то 2Ф(t)=0,95; Ф(t)=0,475 и t=1,96. Следовательно, n= 4

3Пример 10. При выборочном опросе 100 жителей поселка о количестве поездок по железной дороге, совершаемых ими в течение месяца, получены следующие данные:

Число поездок	0-3	3-6	6-9	9-12	12-15	15-18	18-21	21-24	24-27	27-30	Итого
Число жителей	6	9	15	19	20	14	9	5	2	1	100

Требуется:

• Построить эмпирическую функцию распределения случайной величины Х - количества поездок в месяц для наугад взятого жителя поселка;

• Найти доверительный интервал для оценки с надежностью 0,95 среднего значения случайной величины Х.

Решение.

• Данная величина Х является дискретной, а ее эмпирическая функция распределения - ступенчатой. Приближенно можно представить данные обследования в следующем виде:

Таблица 1

Выборочные значения	1,5	4,5	7,5	10,5	13,5	16,5	19,5	22,5	25,5	28,5	Итого
Частоты	6	9	15	19	20	14	9	5	2	1	100

В качестве выборочных значений взяты середины интервалов.

Для каждого выборочного значения х найдем кумулятивную частоту n_х - сумму частот для выборочных значений £ х, и эмпирическую функцию распределения

F*(x) = n_x /n, где n = 100

Таблица 2

х	1,5	4,5	7,5	10,5	13,5	16,5	19,5	22,5	25,5	28,5
nх	6	15	30	49	69	83	92	97	99	100
F*(х)	0,06	0,15	0,30	0,49	0,69	0,83	0,92	0,97	0,99	1

Построим график функции F*{х), исходя из полученной таблицы 2 :

• пусть х₁,...,х₁₀, - выборочные значения, а n₁,...,n₁₀ - их частоты (из табл.1).

Найдем выборочную среднюю:

Так как значение n=100 достаточно велико, то генеральную дисперсию оценим по формуле

откуда s » 5,9.

Задачу построения доверительного интервала решим приближенно, считая, что оценка распределена по нормальному закону (для этого n=100 достаточно велико).

В этом случае доверительный интервал покрывающий неизвестный параметр a=m_x c вероятностью 0,95 равен

,

где значение tg ищется по таблице 3 приложений tg=t(g,n) по заданным g и n.

Имеем, tg=t(0,95,100)=1,984.

Тогда

.

Отсюда получаем доверительный интервал

.

Таким образом, в среднем в 95 случаях из 100 интервал (11,13; 13,47) накрывает среднее число поездок в месяц для случайно выбранного жителя поселка.4

3Пример 11. Выборочная проверка стоимости двухкомнатных квартир (тыс.руб.) дала следующие результаты.

78,0	76,5	78,5	83,5	81,0	84,5	79,0	87,0	80,5	78,5
83,0	81,0	80,5	78,0	83,0	89,0	89,3	85,0	82,0	84,0
79,0	82,5	83,0	79,5	78,5	79,5	81,1	89,0	91,0	83,0
84,5	86,0	84,0	83,0	84,5	82,5	87,0	84,5	85,0	80,5
84,0	83,5	84,5	85,5	87,0	83,5	85,0	78,5	86,0	82,5
82,0	83,0	80,0	82,0	79,0	82,5	87,0	84,0	85,5	83,0

Требуется:

• Составить статистическое распределение выборки.

• Разбив выборку на k классов (k=1+3,22 ×lgn), построить вариационный ряд, соответствующий этому разбиению. Построить гистограмму относительных частот.

• Вычислить для данной выборки несмещенные оценки математического ожидания, дисперсии, показателей асимметрии и эксцесса, коэффициент вариации.

• С помощью критерия Пирсона проверить гипотезу о нормальном распределении случайной величины Х – стоимости квартиры при уровне значимости a=0,05.

• Построить график плотности нормального распределения с параметрами и s на том же чертеже, где и гистограмма.

• Найти доверительные интервалы для математического ожидания и среднего квадратического отклонения с надежностью g=0,95.

Решение.

• Найдем статистическое распределение выборки.

xi	76,5	78,0	78,5	79,0	79,5	80,0	80,5	81,0	81,1	82,0	82,5	83,0	83,5
ni	1	2	4	3	2	1	3	2	1	3	4	7	3

84,0	84,5	85,0	85,5	86,0	87,0	89,0	89,5	91,0
4	5	3	2	2	4	2	1	1

Объем выборки

• Размах выборки R=x_max-x_min=91,0-76,5=14,5. Так как число классов k=1+3,22×lgn=1+3,22×lg60»7, то длина частичного интервала

Для построения гистограммы относительных частот составим таблицу.

Номер интервала i	Частичный интервал xi - хi+1	Сумма частот вариант частичного интервала ni	Относительная частота	Плотность относительной частоты
1	76,5-78,57	7	7/60	0,056
2	78,57-80,64	9	9/60	0,072
3	80,64-82,71	10	10/60	0,081
4	82,71-84,78	19	19/60	0,153
5	84,78-86,85	7	7/60	0,056
6	86,85-88,92	4	4/60	0,032
7	88,92-91,0	4	4/60	0,032

• Найдем несмещенную оценку математического ожидания, т.е. выборочную cреднюю (76,5×1+78,0×2+78,5×4+79,0×3+79,5×2+80,0×1+80,5×3+81,0×2+81,1×1+82,0×3+82,5×4+83,0×7+83,5×3+84,0×4+84,5×5+85,0×3+85,5×2+86,0×2+87,0××4++89,0×2+89,5×1+91,0×1)= .

Чтобы найти несмещенные оценки дисперсии, показателей асимметрии и эксцесса, коэффициент вариации, составим таблицу.

Итак,

• Чтобы с помощью критерия Пирсона проверить гипотезу о нормальном распределении случайной величины Х – стоимости квартиры, нужно вычислить теоретические частоты

.

Для этого составим таблицу

(См.таблицу 2 приложения )

Замечание. Интервалы, содержащие малочисленные эмпирические частоты (n_i<5) следует объединить, а соответствующие частоты сложить.

Итак, получим таблицу

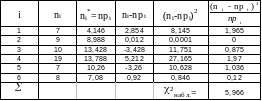
По табл. критических точек распределения c² находим c²_кр=c²(0,05;3)=7,82, т.к. уровень значимости a=0,05 по условию, а число степеней свободы k=m-s=6-3=3, потому что после объединения интервалов число интервалов равно m=6 и s=3. (См. таблицу 5 приложения)

Т.к. c²_набл<c²_кр, то нет оснований отклонить гипотезу о нормальном распределении генеральной совокупности.

• Чтобы построить график плотности нормального распределения c параметрами и S, заполним следующую таблицу.

Для нормального распределения с параметрами , s=S плотность вероятности . Т.к. есть таблица значений функции 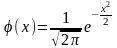, то .

(См. таблицу 1 приложения)

Построим график плотности вероятности f(х) на том же чертеже, что и гистограмма: соединим последовательно точки ( ; f( )), где i= .

Доверительный интервал для m_х равен .

Т.к. g=0,95, то по таблице tg=t(g;n)=t(0,95;60)=2,00 (См. таблицу 3 приложения).

Итак,

– доверительный интервал для параметра m_х.

Доверительный интервал для s равен: (S(1-q); S(1+q)),

т.к. q = q(g, n)=q(0,95; 60)=0,19<1. (См. таблицу 4 приложения).

Итак, (3,409(1-0,19); 3,409(1+0,19))=(2,76; 4,05) – доверительный интервал для параметра s.4

Вопросы для самопроверки.

• Доверительный интервал и доверительная вероятность (надежность), их взаимосвязь.

• Генеральная и выборочная доли. Отклонение выборочной доли от постоянной вероятности в независимых испытаниях.

• Доверительный интервал для генеральной доли.

• Теоретические распределения, используемые при интервальном оценивании, условия их использования.

• Интервальная оценка математического ожидания нормального распределения при известном и при неизвестном среднеквадратическом отклонении этого распределения.

• Учет объема выборки при интервальном оценивании.

• Общая схема статистической проверки гипотез.

• Понятия о уровне значимости и критической области.

• Понятие о мощности критерия проверки гипотез.

• Взаимосвязь уровня значимости и мощности критерия.

• Проверка гипотез о равенстве средних и дисперсии.

• Проверка гипотезы о виде закона распределения.

• Понятие о критериях согласия.

• Критерий Пирсона.

• Оценки показателей асимметрии и эксцесса, их смысл.

• Доверительные интервалы для математического ожидания и среднего квадратического отклонения.