2011
Аналіз генераторів псевдовипадкових чисел
КИЇВСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ ІМЕНІ ТАРАСА ШЕВЧЕНКА
Звіт
з лабораторної роботи №2
з програмування
«Аналіз генераторів псевдовипадкових чисел»
Виконав:
Студент першого курсу
Факультету кібернетики
Групи К-15
Цицюра О.В.
Перевірив:
Коваль Ю.В
Київ
13.12.2011
Перелік розділів
Умова роботи 3
Постановка задачі 4
Тести 6
Побудова алгоритму 7
Проектування програми 9
Тестування 13
Інструкція користувача 14
Список використаної літератури 15
Додатки 16
Умова роботи
Написати програму, що тестує генератори псевдовипадкових чисел. Реалізувати інтерфейс програми.
Постановка задачі
Вхідні дані: верхня(k) межа генерування псевдовипадкових чисел, кількість елементів(T), тип генератора псевдовипадкових чисел.
Вихідні дані: спектр, гістограма, значення дисперсії у відсотках до M∂, згенерований HTML файл, який демонструє двовимірний тест генератора псевдовипадкових чисел.
Дисперсія (англ. Variance) є мірою відхилення значень випадкової величини від центру розподілу. Більші значення дисперсії свідчать про більші відхилення значень випадкової величини від центру розподілу.
Означення дисперсії
Дисперсією випадкової величини X називається математичне сподівання квадрата відхилення цієї величини від її математичного сподівання (середнього значення). Дисперсія є центральним моментом другого порядку.
Нехай
випадкова змінна X може
набувати значення 
відповідно
з ймовірностями 
причому 
.
Дисперсія дискретної випадкової величини X має такий вигляд:
,
де
і
називається стандартним
відхиленням величини X від
її середнього
значення 
;
—
це оператор дисперсії
випадкової величини.
Якщо випадкова величина
задана густиною
імовірності, тоді дисперсія виглядає
так:
,
де
,
тобто це середнє значення величини 
;
—
функція
густини імовірності.
Гістограма (від грец. histos, тут стовп + grаmma — межа, буква, написання) — спосіб графічного представлення табличних даних. Являє собою діаграму, що складається з прямокутників без розривів між ними.
Html теги.
Елементи HTML — основні компоненти мови розмітки HTML. HTML-документ складається з головного елементу html, до змісту якого додаються інші елементи.
Кожен елемент має свою унікальну назву, яка записується латинськими літерами і не чутлива до їх регістру. В загальному вигляді елемент має три складові: теги (початковий<…> та кінцевий</…>),атрибути та зміст (контент). Тег — це назва елементу, записана у кутових дужках (< >), яка задає певну властивість для змісту цього тегу. Атрибути задають технічну інформацію про елемент. Зміст елементу — це вся необхідна текстова та графічна інформація документу, яка буде відтворюватися браузером на екрані.
<HTML>…</HTML> теги, що визначають початок і кінець документа.
<Body>…</Body> ця секція містить всю видиму частину web-сторінки.
Теги <table>… </ table> - оголошують про створення HTML таблиці. border = "1" - встановлює границю HTML таблиці та її комірок в 1 піксель. Якщо атрибут border відсутній або має значення 0 - меж не буде. Теги <tr>…</ tr> - визначають табличний ряд. Теги <td> …</ td> - визначають клітинку HTML таблиці. cellspacing = "0" - визначає відстань між комірками таблиць, а також між межами комірок і межею таблиці. cellpadding = "8" - простір між межею комірки і її вмістом. background-color: - визначає колір фону. Символ пробілу в цьому місці заповнює порожній простір усередині осередку.
Умова:
Програма повинна уміти працювати з n вимірними просторами, виводити на екран гістограму та генерувати HTML файл.
Тести
Вхід:
k=5;
T=50;
n=1;
Вхід:
k=5;
T=50;
n=2;
Вхід:
k=3;
T=500;
N=3;
Побудова алгоритму
Спектр будемо зберігати за допомогою масиву, тобто кожен елемент спектру будемо ставити у відповідність елементу масиву.
Дисперсія – міра розкиду спектру. Будемо рахувати середньоквадратичне значення дисперсії за такою формулою:
Де, D – дисперсія, S[] – масив псевдовипадкових значень, S – середнє значення, k-кількість елементів масиву S[]. Значення дисперсії повинні бути більшими за нуль.
Оскільки ми працюємо з цілими числами, то й корінь потрібно добути цілим, для цього використаємо метод Ньютона, який заключається у формулі:
де n - підкореневий вираз, з якого потрібно добути цілий корінь, xk+1 можливий корінь.
У
цій формулі початкове значеня
[x0]
буде
рівне підкореневому виразу,
тобто
[n].
Ця формула задає рекурсію,
дно
якої
досягається
тоді, коли
.
Тобто
коли наступний член послідовності буде
відрізнятися
від
попереднього на 1.
Оскільки
то
модуль можна прибрати. За допомогою
цієї формуль ми можемо лише наближено
знайти значення корення, точніше ми
знайдемо
.
Генератор псевдовипадкових чисел. Генератор випадкових чисел буде шукати остачу від ділення отриманого числа з послідовності Фібоначчі.
Одновимірне тестування можна зобразити у вигляді гістограми, для цього циклом «for» будемо виводити у рядок [n]-кількість ’*’.
Двовимірне тестування будемо зображати у вигляді HTML-таблиці, яку будемо створювати у файлі “index.html” використовуючи теги <TABLE>, <TR>, <TD>, <BODY>, <HTML>.
Проектування програми
Для написання програми використаємо мову C та інтегроване середовище Dew-C++ 4.9.9.2.
Для генерування чисел будемо використовувати послідовність чисел Фібоначчі. Використовуючи формулу: Rn Fib() % k.
Де, n-номер числа, k-константа.
Fib()- n-те число Фібаначчі, або n-тий лишок числа Фібоначчі(це тому що числа Фібоначчі досить швидко ростуть і у першому випадку послідовність є неправильною, тому що вони зберігаються у вигляді Rn (Fib() % 232) % k), а якщо брати n-тий лишок, то формула має вигляд Rn ( (Fn-1 % k + Fn-2 % k) % k).
У масиві A[] будемо зберігати послідовність згенерованих псевдовипадкових чисел, для подальщої їх обробки.
for(i=T;i--;(*(A+T-i-1))=r(k));
За допомогою цього циклу запишемо у масив A[] Т-згенерованих псевдовипадкових чисел.
Для одновимірного тестування будемо використовувати масив B[], у який будемо записувати кількість повторів кожного числа у масиві A[].
for(i=T;(i--)>(n-1);B[l(n,A+T-i)]++);
де n-кількість просторів, l(int n, int* x) – функція, яка визначає номер елемента з n-вимірного аналізу у лініарізованому масиві.
Наприклад, (k-кількість елементів у одновимірному масиві):
(2,3,9,7)=[
{ (
2
*
k + 3)
* k + 9 } * k + 7 ] =
Для спостереження за двовимірним аналізом використовуємо HTML-таблиці. Яку ми записуємо у створений файл “index.html” використовуючи такий код:
FILE *<файлова зміна>;
fp=fopen(<імя файлу>,<метод відкривання>);
fprintf(<файлова змінна>,<текст>);
fclose(<файлова змінна>);
Таким чином у файл записуємо такий код:
<HTML>
<body>
<table width="100%" height="100%" border="0" cellspacing="1" cellpadding="4">
<tr>
<td align="middle" bgcolor=#000000> </td>
<td align="middle" bgcolor=#66CDAA> </td>
</tr>
<tr>
<td align="middle" bgcolor=#66CDAA> </td>
<td align="middle" bgcolor=#66CDAA> </td>
</tr>
</table>
</body>
</HTML>
Таблиця має схему
<table>
<tr><td></td>…<td></td></tr>
…
<tr><td></td>…<td></td></tr>
</table>
де <tr>…</tr> рядок таблиці, <td></td> - комірка рядка таблиці.
Інтерфейс було реалізовано за допомогою функції порівняння двох рядків:
int eq(char* S1, char* S2){
int i;
i=0;
while(S1[i]!='\n' || S2[i]!=' '){
if(S1[i]!=S2[i]) return 0;
i++;
}
return 1;
}
Ця функція повертає 1, якщо два вхідні слова одинакові, і 0 якщо ні.
Поки небуло введено команди «exit» цикл працює. У тілі циклу ми зчитуємо наступну команду і по можливості виконуємо її.
while(!eq(M,"exit ")){
pid();
ngets(50,M);
...
if(!eq(M,"exit ")) printf(" Wrong command!!!\n");
}
У тілі циклу ми також перевіємо яку команду було введенно. Це перевіряється за допомогою if(приклад перевіряння команди «read k»):
if (eq(M,"read k ")){
pid();
printf("%s","k= ");k=in();
ngets(50,M);
if (k>50) {
k=50;
printf(" Maybe you want to have k=50.\n");
}
else printf(" Operation was done sucessfully.\n");
rk=1;}
Т
естування
Вхід:
k=5;
T=50;
n=1;
Вихід: >>>>>>>>>>>>>>>>>>>>
Вхід:
k=5;
T=50;
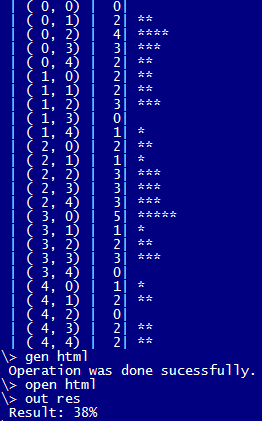n=2;
Вихід:
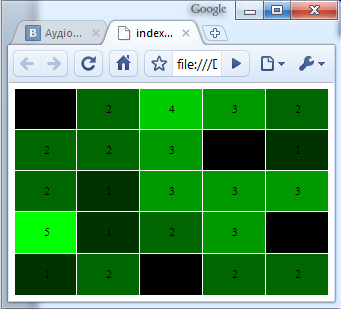
Вхід:
k=3;
T=500;
N=3;
Вихід:
Інструкція користувача