8. Написать формулу Биномиального закона распределения.

Пусть случайная величина - число появления события в независимых повторных испытаниях, в каждом из которых событие может наступить с вероятностью ( и следовательно не наступить с вероятностью . Закон распределения этой случайной величины называется биномиальным.

Случайная величина , распределенная по биномиальному закону, характеризуется следующим рядом распределения (табл. 1):

	0	1	2	…	m	…	n

В этой таблице: - возможные значения случайной величины ; , , …, , …, - вероятности того, примет эти значения. Вероятности находят по формуле Бернулли: (1).

Математическое ожидание, дисперсия и среднее квадратическое отклонение случайной величины, подчиняющейся биномиальному закону распределения, находят, соответственно по формулам:

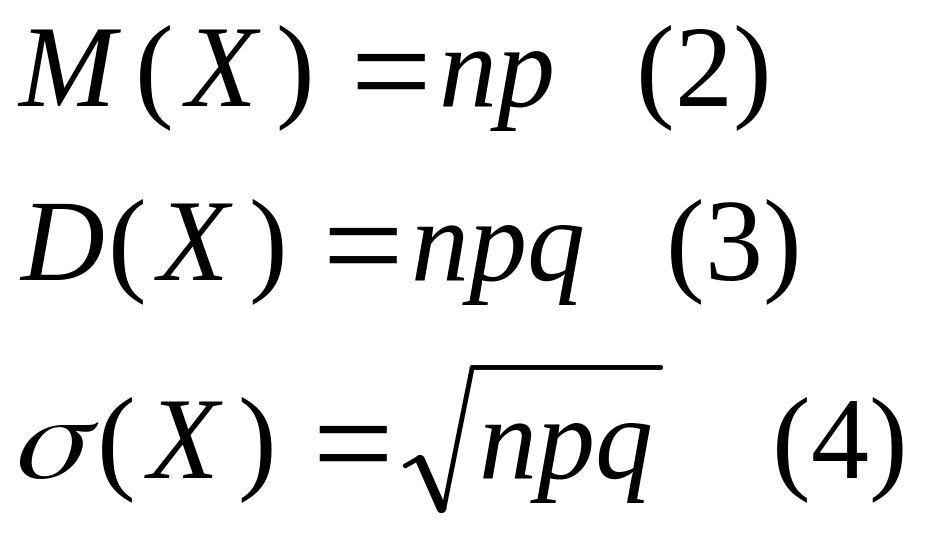
9. Перечислить свойства плотности вероятности.

Непрерывная случайная величина может быть задана функцией распределения (называемой также интегральной функцией распределения)

или же плотностью распределения вероятностей (называемой также дифференциальной функцией распределения):

(1)

Равенство (1) имеет место в точках непрерывности функции .

Зная плотность распределения вероятностей, можно найти функцию распределения:

(2).

Свойства плотности распределения вероятностей:

1.

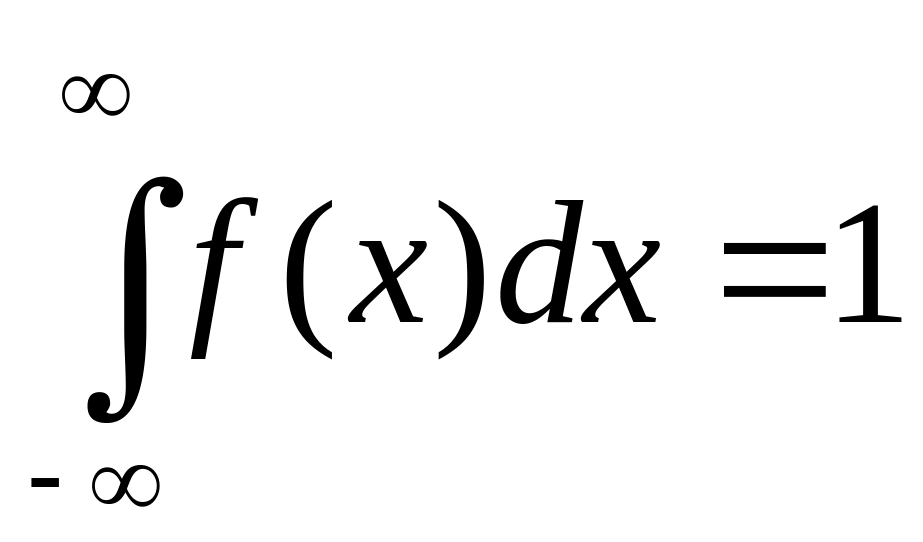2. . (3)

В частности, если все возможные значения случайной величины принадлежат интервалу (a, b), то

.

Вероятность того, что непрерывная случайная величина примет значение , определяется равенствами:

. (4).

10. Написать формулу нормального закона распределения.

Случайная величина распределена по нормальному закону, если ее плотность распределения вероятностей

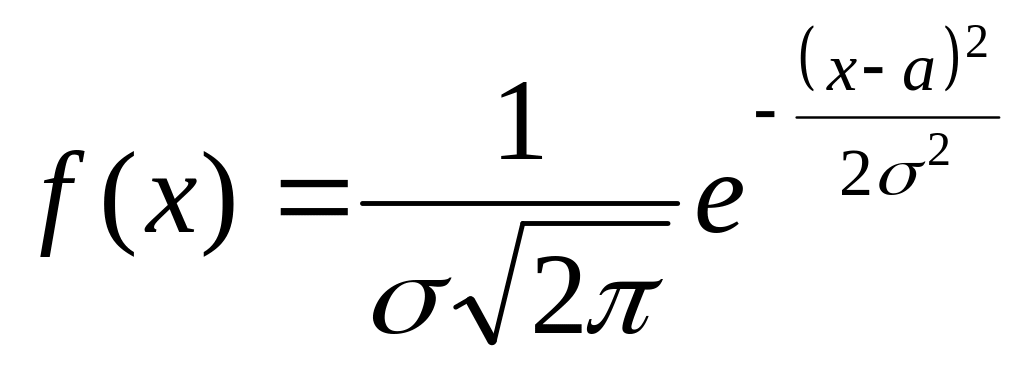
(1), где - математическое ожидание, - среднее квадратическое отклонение .

Вероятность того, что примет значение, принадлежащее интервалу , равна

(2), где

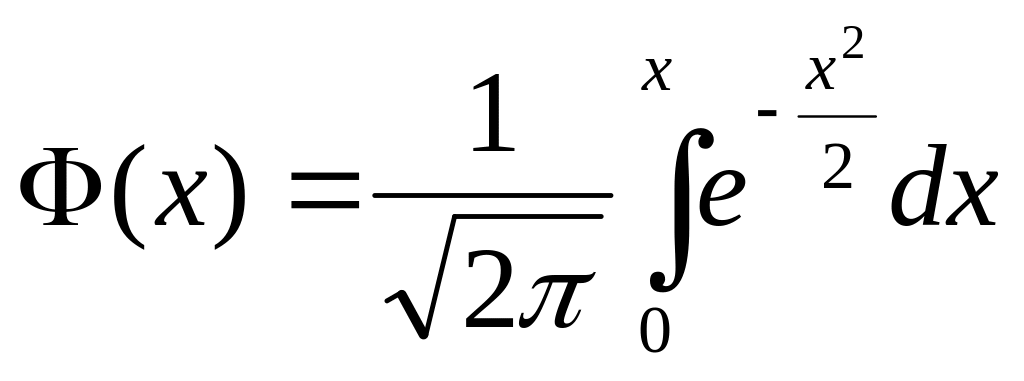-функция Лапласа.

Вероятность того, что абсолютная величина отклонения нормально распределенной случайной величины от ее математического ожидания не превысит положительного числа , равна

(3).

11. Дать определение вариационного ряда.

Числа, показывающие, сколько раз встречаются варианты из данного интервала, называются частотами (обозначаем n_i,), а отношение их к общему числу наблюдений — частностями или относительными частотами, т.е. w_i = n_i/п. Частоты и частости называют-

весами.

Определение. Вариационным рядом называется ранжи­рованный в порядке возрастания (или убывания) ряд вариантов с соответствующими им весами (частотами или частостями.

12. Что характеризует коэффициент корреляции.

Основными задачами при изучении корреляционных зависимо­стей являются: 1) отыскание математической формулы, которая бы выражала эту зависимость у от х; 2) измерение тесноты такой зави­симости.

Решение первой задачи, т.е. определение формы связи с после­дующим отысканием параметров уравнения, называется нахождени­ем уравнения связи (уравнения регрессии). Показатели, рассматрива­емые как функция х, обозначают (читается: «игрек, выравнен­ный по икс»).

Возможны различные формы связи:

1. прямолинейная: ;

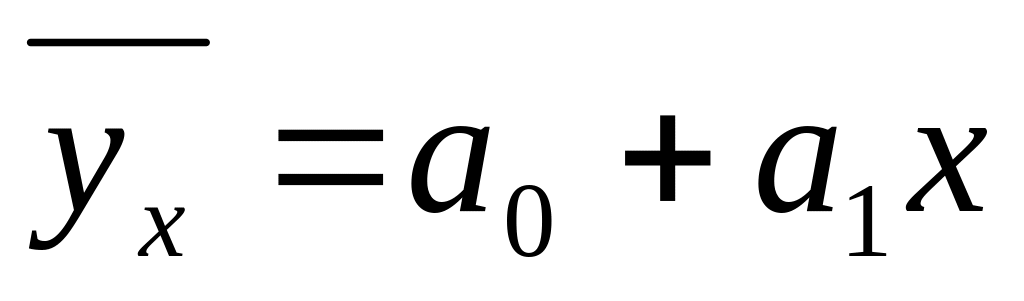2. криволинейная в виде:

а) параболы второго порядка (или выс­ших порядков);

б) гиперболы ;

в) показательной функции и т.д.

Параметры для всех уравнений связи чаще всего определяют из так называемой системы нормальных уравнений, отвечающих требованию «метода наименьших квадратов» (МНК). Это требование можно записать как или при линейной зависимости, , т.е. требуется определить, при каких значениях параметров и сумма квадратов отклонений у от будет минимальной. Найдя частные производные указанной суммы по и , и приравняв их к нулю, легко записать систему уравнений, решение которой и дает параметры искомой функции т.е. уравнения регрессии.

Так, система нормальных уравнений при линейной зависимости имеет вид

Если связь выражена параболой второго порядка

то система нормальных уравнений для отыскания параметров , и выглядит следующим образом:

Вторая - задача — измерение тесноты зависимости — для всех форм связи может быть решена с помощью исчисления теоретического корреляционного отношения ():

где — дисперсия в ряду выровненных значений результативного показателя ;

дисперсия в ряду фактических значений у.

Так как дисперсия отражает вариацию в ряду только за счет вариации фактора х, а дисперсия отражает вариацию у за счет всех факторов, то их отношение, именуемое теоретическим коэффициентом детерминации, показывает, какой удельный вес в общей дисперсии ряда у занимает дисперсия, вызываемая вариацией фактора х. Квадратный корень из отношения этих дисперсий дает нам теоретическое корреляционное отношение. Если , то это означает, что роль других факторов в вариации у сведена на нет, и отношение означает полную зависимость вариации у от х. Если , то это означает, что вариация х никак не влияет на вариацию у, и в этом случае . Следовательно, максимальное значение, которое может принимать корреляционное отношение, равно 1, минимальное значение — 0.