Дать определение формулы полной вероятности и формулы Бейеса.
Формула полной вероятности и формула Бейеса
Вероятность
события
,
которое может наступить при условии
появления одного из n
несовместных событий (гипотез)
(i=1,2,
…,n)
образующих полную группу, находят по
формуле полной вероятности:
(1)
В
этой формуле
- вероятность события
;
- вероятность события
,
-
вероятность события
при условии, что событие
наступило;
-
сумма произведения вероятностей
каждого из событий
на соответствующую ей условную вероятность
.
Сумма
вероятностей гипотез
.
Пусть
событие
может наступить лишь при условии
появления одного из несовместных событий
(гипотез)
,
которые образуют полную группу событий.
Если событие
уже произошло, то вероятности гипотез
могут быть переоценены по формуле
Бейеса:
,
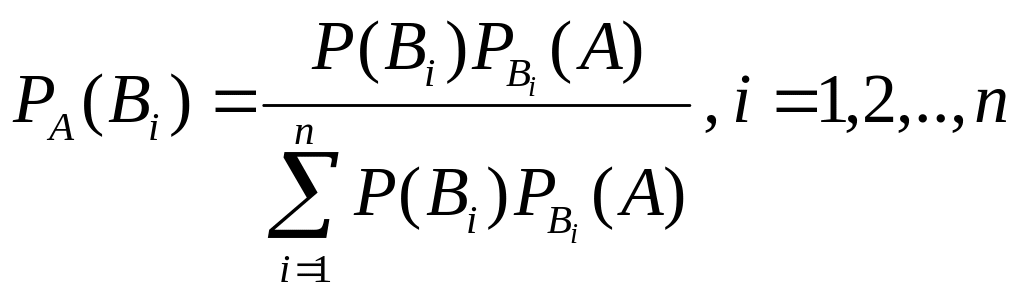(2).
В
этой формуле
-
вероятность события
,
-
условная вероятность события
при условии, что событие
наступило;
- вероятность события
;
- условная вероятность события
,
вычисленная при условии, что событие
произошло.
Написать формулу Бернулли.
Пусть
производиться n
независимых испытаний, в каждом из
которых может появиться или не появиться
событие
.
Вероятность наступления события
в каждом испытании постоянна и равна
.
Вероятность появления события
в
испытаниях ровно
раз (безразлично, в какой последовательности)
находят по формуле Бернулли
. (1)
В
этой формуле
- вероятность появления события
в одном испытании;
вероятность
непоявления события
в одном испытании;
- общее число производимых испытаний,
в которых появится событие
;
- вероятность того, что событие
появиться ровно
раз в
испытаниях.
Перечислить числовые характеристики дискретных случайных величин.
Математическое
ожидание дискретной случайной величины
,
имеющей конечное число возможных
значений, равно
,
(1).
Математическое ожидание дискретной случайной величины , имеющей бесконечное число возможных значений, равно
,
(2).
Причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.
В
формулах (1) и (2):
- возможные значения случайной величины
,
- вероятности того, что случайная величина
примет эти значения.
Свойства математического ожидания:
1.
(3).
Где
-
постоянная величина.
2.
,
(4).
Где
=const.
3.
(5).
Где
и
- две любые случайные величины.
4.
,
(6).
Где и - две независимые случайные величины.
Дисперсия случайной величины определяется равенством
,
(7)
Или равносильным ему равенством
(8).
Дисперсию дискретной случайной величины, имеющей конечное число возможных значений, можно вычислять по формуле
,
(9).
Соответствующей формуле (7), или по формуле
, (10),
соответствующей формуле (8).
Свойства дисперсии:
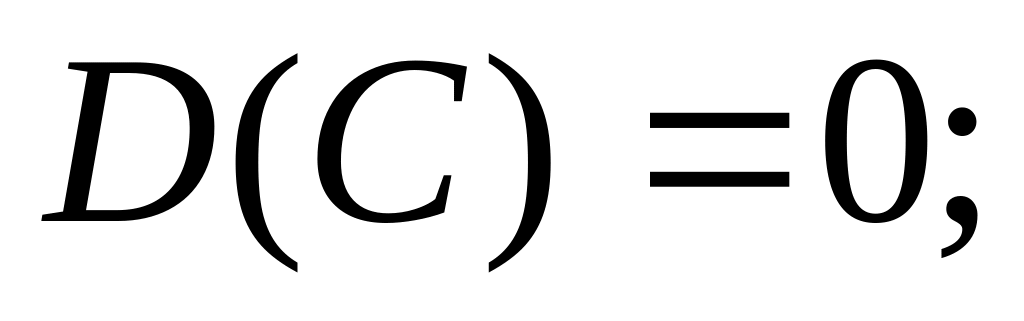(11)
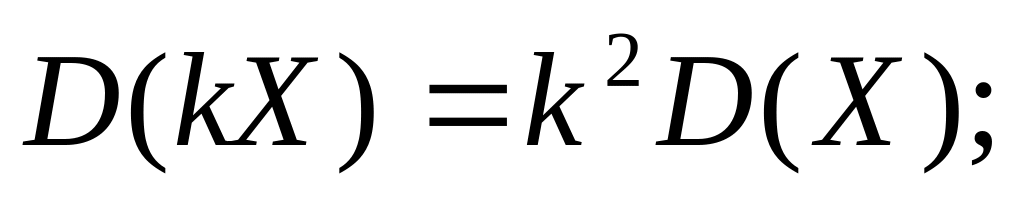(12)
;
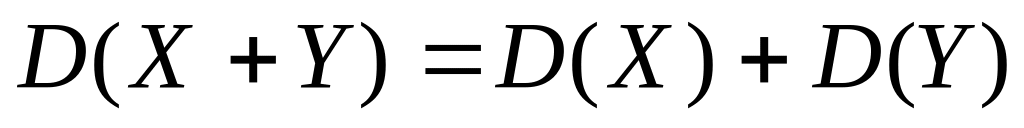(13), где
и
- две независимые случайные величины.
Среднее квадратическое отклонение случайной величины равно
(14).
Перечислить числовые характеристики непрерывных случайных величин.
Математическое
непрерывной случайной величины
,
значения которой принадлежат всей оси
,
определяется равенством
, (1)
- плотность распределения вероятностей
величины
.
Предполагается, что несобственный
интеграл в формуле (1) сходится абсолютно.
В
частности, если все возможные значения
принадлежат интервалу
,
то
(2)
Дисперсия непрерывной случайной величины , значения которой принадлежат всей оси , определяется равенством
(3)
Или равносильным ему равенством
(4)
Предполагается, что несобственные интегралы в формулах (3) и (4) сходятся абсолютно.
В частности, если все возможные значения принадлежат интервалу , то
(5)
Или
(6)
Среднее квадратическое отклонение непрерывной случайной величины определяется также, как и дискретной случайной величины:
Мода
непрерывной случайной величины
-
это ее возможное значение, которому
соответствует локальный максимум
дифференциальной функции распределения.
Медиана
непрерывной случайной величины
определяется
на основании равенства
(7).